Pues bien, ¿qué pasa si decimos (a ojo) que es un seno, con un periodo constantemente creciente (en función de X), es decir, una fórmula como ésta:
General (de dónde venimos):
Y=sin( K*X+T)
Ahora decimos que el parámetro K también depende de X. Todo el tiempo está aumentando o disminuyendo. La pregunta que surge es: ¿es lineal? Para empezar, supongo que de forma lineal. Entonces es A*X+B (fórmula de la línea). Sustituido en la fórmula original, obtenemos
Y=sin((A*X+B)*X+T)=sin(A*X^2+BX+T).
Aquí tenemos un punto de partida. Polinomio bajo el signo del seno. Ejecutar la regresión.... etc. - Espero haberlo explicado claramente. Me gustaría hacerte un programa en Matlab, pero no tengo tiempo, tendrás que hacerlo tú.
Permítanme explicar un poco para qué sirve esto. Tengo una idea para TC basada en un predicado. De conocidos para mí y más o menos disponibles son Fourier y regresión. Aplicado a Fourier. El supuesto subyacente es que los parámetros son estacionarios. En una onda sinusoidal normal, todo parece estar bien
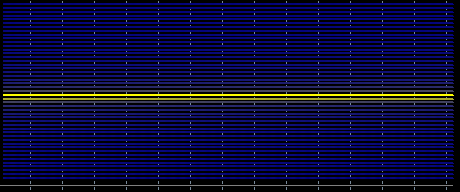
Pero si tomamos un periodo que varía suavemente, el espectro se difumina
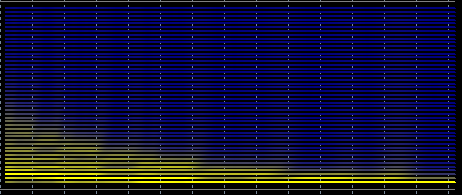
y por lo tanto no se puede obtener una predicción adecuada.
Tampoco pude conseguir nada bueno en la regresión.
Por lo tanto, tenemos que buscar otros métodos que sean más "adaptativos" o algo así. Eso es lo que quería saber.
Tiene una curva suave. Por lo tanto, los métodos de análisis diferencial son aplicables a ella. Incluso sin saber que se trata de un seno con periodo variable, se puede utilizar una expansión en serie de Taylor con retención de los primeros términos. A continuación, puede utilizarla para predecir el valor de una referencia futura sustituyendo algunos términos anteriores en la fórmula. Le aseguro que el resultado le sorprenderá por su precisión de predicción. El error será cero.
Y no funcionará para las series de precios, porque en la descomposición en RF obtendrás PDF y no tendrás que predecir un conteo hacia adelante, sino para el número de conteos que se ajuste a la escala de PDF y ahí es donde saltará el error de predicción.
No se puede engañar a la naturaleza.
Y todo esto no funcionará para las series de precios, porque al descomponer en RF obtendrá una FZ y tendrá que predecir no un recuento hacia adelante sino el número de recuentos que encajan en la escala de la FZ y es a esta distancia donde el error de predicción aumentará drásticamente.
No se puede engañar a la naturaleza.
Eso es comprensible. Pero se puede suponer que los parámetros no cambian durante un periodo de tiempo. Con la imagen superior quería mostrar que el resultado puede ser malo no sólo por la no estacionalidad, sino también por un método inadecuado.
Eso está claro. Pero es posible suponer que los parámetros no cambian durante algún tiempo. Con la imagen superior quería mostrar que el resultado puede ser malo no sólo por la no estacionalidad, sino también por un método inadecuado.
La hipótesis de un mercado estacionario nunca se ha confirmado. Por lo tanto, no se puede suponer que los parámetros se mantengan constantes a lo largo de cualquier horizonte temporal, por pequeño que sea.
Permítanme explicar un poco para qué sirve esto. Tengo una idea para TC basada en un predicado. De conocidos para mí y más o menos disponibles son Fourier y regresión. Aplicado a Fourier. El supuesto subyacente es que los parámetros son estacionarios. En una onda sinusoidal normal, todo parece estar bien
Pero si tomamos un periodo que varía suavemente, el espectro se difumina
y por lo tanto no se puede obtener una predicción adecuada.
Tampoco pude conseguir nada bueno en la regresión.
Por lo tanto, tenemos que buscar otros métodos que sean más "adaptativos" o algo así. Eso es lo que quería saber.
¿qué puede hacer una ondícula?
ZS: Hice un .dll con el código de BaseGroup.ru para MT5, pero todavía no he encontrado ningún uso práctico http://imglink.ru/pictures/18-01-12/4e3891b89673e8f79e194b5a86a25d41.jpg
La hipótesis de un mercado estacionario nunca se ha confirmado. Por lo tanto, no se puede suponer que los parámetros permanezcan constantes en cualquier horizonte temporal, por pequeño que sea.
No me refiero a la estacionariedad completa, pero quizá haya tramos en los que los parámetros sean más o menos estables. Si no, cómo explicar que las estrategias pueden funcionar durante algún tiempo. Hay un enfoque en el que se hacen varias estrategias y se cambia entre ellas, la cuestión es cómo determinar el momento del cambio.
www.https://www.mql5.com/ru/forum/127297 Aquí hay pruebas indirectas de la previsibilidad temporal.
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Hay un cuadro como este:
¿Qué metodología puede extrapolar una serie como ésta?
¿Podría alguien poner esto en una red neuronal para un experimento?