You are missing trading opportunities:
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
Registration
Log in
You agree to website policy and terms of use
If you do not have an account, please register
Mrtools, Thank you , but are you sure this is correct ?Please check :https://www.forex-tsd.com/forum/debates-discussions/116-something-interesting-please-post-here/page93#comment_410749 https://www.forex-tsd.com/forum/debates-discussions/116-something-interesting-please-post-here/page93#comment_410818 thanks.
Biddick the smoothing is correct, but can't say that the alb is correct being that the length is an array, and that is what i was changing to get adaptive lookback in the other indicators, but none of them were arrays, so very possible it is not calculating correctly, thanks for bringing that to my attention, but not sure how to fix or if it is needed!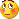
biddick
That picture there (posted by fxbs) is not Phase change index but the codining error I made when I was making it (the "coding error" indicator was posted a few posts before that) and he was trying to find out where exactly did I make an error, so they can not be compared
__________________
MrTools
There is no error in your code. But what happens is that the PCi becomes "too adaptive" - with swing count set to 5 it means that the minimal calculation length for PCI is 5 and a practical maximal calculation length is very, very rarely at the values of the default values of 35 that are used by PCI. I think that the solution for it is to limit minimal and maximal length of calculation - like in the one that I am posting here. Here is a comparison of smoothed PCI (upper) to adaptive look-back PCI smoothed (lower)So, in this one, it is a kind of "controlled adaptivity" instead of "total adaptivity"__________________
PS: the adaptivity is in the Phase change index calculation length, not in the smoothing part : smoothing is adaptive already and does not need additional adaptivity
Mladen ... Mrtools
Mladen ... Mrtools there any way to make "Triangular ray band centered adr" autoarreglabe for use in different time frames: in H1 works well but, M15, M30, ... not going well.
Thanks
You can check the web. you sent, or be more precise ...
"Triangular adr centered band ray" automation for M15,...M30
...not for H1
changing look-back window: continued
A simple RSI or momentum can become extremely powerful if you find a good way to adjust the look-back window. As an illustration, I used the zig zag swing as an input for the number of periods (bottom window on the chart) to calculate a SMA, momentum (upper window) and RSI (middle window). As you can see, they are way better like this compared to the standard 14 periods setting. You could simply smooth the momentum and then trade the slope.
Here's an overview of different methods:
- spectral methods for dominant cycle extraction:
* FFT
* MESA
* Goertzel
* other filter banks
- fractal method:
* CFB by Mark Jurik
- price action:
* swing high/swing low: alb
To add to the list:
by Ehlers:
* Homodyne discriminator (Ehlers doesn't use it any more because it lags 20 bars...)
* Corona Charts
and this one hereby attached using Legendre Polynomials: XCAP_iPolyCycle by Paul A. Griffin from Extrema Capital. I found it on the Tradestation forum (for clients):
https://www.tradestation.com/Discussions/Topic.aspx?Topic_ID=59793
Mladen you think you can make an mq4 version of this Tradestation indicator? Or is this even out of your league?
I have found this Polynomials: XCAP_iPolyCycle tradestation formula on th net
Mladen
Can you adjust adjust zigzag swing as the look-back period for Gann-high low indicator please?Thank you.
This a converted and adapted for metatrader indicator posted by Mrm and biddick. Best description is the one from the original author of the indicator - Paul A. Griffin Description is taken form the eld but ii is exactly the same in the txt posted by biddick
________________________________
Introduction:
This is an example of what can be done by combining Legendre polynomials and analytic signals. I get a way of determining a smooth period and relative adaptive strength indicator without adding time lag.
This indicator displays the following:
1. The Least Squares fit of a polynomial to a DC subtracted time series - a best fit to a cycle.
2. The normalized analytic signal of the cycle (signal and quadrature).
3. The Phase shift of the analytic signal per bar.
4. The Period and HalfPeriod lengths, in bars of the current cycle.
5. A relative strength indicator of the time series over the cycle length. That is, adaptive relative strength over the cycle length.
The Relative Strength Indicator, is adaptive to the time series, and it can be smoothed by increasing the length of decreasing the number of degrees of freedom.
Other adaptive indicators based upon the period and can be similarly constructed.
There is some new math here, so I have broken the story up into 5 Parts:
Part 1:
Any time series can be decomposed into a orthogonal set of polynomials [1,2,3].
This is just math and here are some good references:
[1] Legendre polynomials - Wikipedia, the free encyclopedia
[2] https://www.tradestation.com/Discussions/Topic.aspx?Topic_ID=59250
[3] Peter Seffen, "On Digital Smoothing Filters: A Brief Review of Closed Form Solutions and Two New Filter Approaches", ircuits Systems Signal Process, Vol. 5, No 2, 1986
I gave some thought to what should be done with ths and came to the conclusion that they can be used for basic smoothing of time series. For the analysis below, I decompose a time series into a low number of degrees of freedom and discard the zero mode to introduce smoothing.
That is:
time series => c_1 t + c_2 t^2 ... c_Max t^Max
This is the cycle. By construction, the cycle does not have a zero mode and more physically, I am defining the "Trend" to be the zero mode.
The data for the cycle and the fit of the cycle can be viewed by setting
ShowDataAndFit = TRUE;
There, you will see the fit of the last bar as well as the time series of the leading edge of the fits. If you don't know what I mean by the "leading edge", please see some of the postings in [2]. The leading edges are in grayscale, and the fit of the last bar is in color.
I have choosen Length = 17 and Degree = 4 as the default. I am simply making sure by eye that the fit is reasonably good and degree 4 is the lowest polynomial that can represent a sine-like wave, and 17 is the smallest length that lets me calculate the Phase Shift (Part 3 below) using the Hilbert Transform of width=7 (Part 2 below).
Depending upon the fit you make, you will capture different cycles in the data. A fit that is too "smooth" will not see the smaller cycles, and a fit that is too "choppy" will not see the longer ones. The idea is to use the fit to try to suppress the smaller noise cycles while keeping larger signal cycles.
Part 2:
Every time series has an Analytic Signal, defined by applying the Hilbert Transform to it. You can think of the original time series as amplitude * cosine(theta) and the transformed series, called the quadrature, can be thought of as amplitude * sine(theta). By taking the ratio, you can get the angle theta, and this is exactly what was done by John Ehlers in [4]. It lets you get a frequency out of the time series under consideration.
[4] Amazon.com: Rocket Science for Traders: Digital Signal Processing Applications (9780471405672): John F. Ehlers: Books
It helps to have more references to understand this. There is a nice article in Wikipedia[5] on it.
Read the part about the discrete Hilbert Transform:
[5] Hilbert transform: Definition from Answers.com
Also, Answers.com has good information on the Hilbert Transform and links to other concepts:
[6] Hilbert transform: Definition from Answers.com
If you really want to understand how to go from continuous to discrete, look up this article written by Richard Lyons:
[7] www.dspguru.com/info/tutor/QuadSignals.pdf
In the indicator below, I am calculating the normalized analytic signal, which can be written as:
s + i h where i is the imagary number, and s^2 + h^2 = 1;
s= signal = cosine(theta)
h = hilbert transformed signal = quadrature = sine(theta)
The angle is therefore given by theta = arctan(h/s);
The analytic signal leading edge and the fit of the last bar of the cycle can be viewed by setting
ShowAnalyticSignal = TRUE;
The leading edges are in grayscale fit to the last bar is in color. Light (yellow) is the s term, and Dark (orange) is the quadrature (hilbert transform). Note that for every bar, s^2 + h^2 = 1 , by construction.
I am using a width = 7 Hilbert transform, just like Ehlers. (But you can adjust it if you want.) This transform has a 7 bar lag. I have put the lag into the plot statements, so the cycle info should be quite good at displaying minima and maxima (extrema).
Part 3:
The Phase shift is the amount of phase change from bar to bar.
It is a discrete unitary transformation that takes s[1] + i h[1] to s + i h
explicitly, T = (s+ih)*(s[1]-ih[1]) , since s[1]*s[1] + h[1]*h[1] = 1.
writing it out, we find that T = T1 + iT2
where T1 = s*s[1] + h*h[1] and T2 = s*h[1]-h*s[1]
and the phase shift is given by PhaseShift = arctan(T2/T1);
Alas, I have no reference for this, all I doing is finding the rotation what takes the analytic signal at bar [1] to the analytic signal at bar [0]. T is the transfer matrix.
Of interest is the PhaseShift from the closest two bars to the present, given by the bar [7] and bar [8] since I am using a width=7 Hilbert transform, bar [7] is the earliest bar with an analytic signal.
I store the phase shift from bar [7] to bar [8] as a timeseries called PhaseShift. It basically gives you the (7-bar delayed) leading edge the amount of phase angle change in the series.
You can see it by setting
ShowPhaseShift=TRUE
The green points are positve phase shifts and red points are negative pahse shifts.
On most charts, I have looked at, the indicator is mostly green, but occationally, the stock "retrogrades" and red appears. This happens when the cycle is "broken" and the cycle length starts to expand as a trend occurs.
Part 4:
The Period:
The Period is the number of bars required to generate a sum of PhaseShifts equal to 360 degrees.
The halfperiod is the number of bars required to generate a sum of phase shifts equal to 180 degrees. It is usually not equal to 1/2 of the period.
You can see the Period and Halfperiod by setting
ShowPeriod=TRUE
The code is very simple here:
Value1=0;
Value2=0;
while Value1 < barnumber and AbsValue(Value2) < 360 begin
Value2 = Value2 + PhaseShift[Value1];
Value1 = Value1 + 1;
end;
Period = Value1;
The period is sensitive to the input length and degree values but not overly so. Any insight on this would be appreciated.
Part 5:
The Relative Stength indicator:
The Relative Strength is just the current value of the series minus the minimum over the last cycle divided by the maximum - minimum over the last cycle, normalized between +1 and -1.
RelativeStrength = -1 + 2*(Series-Min)/(Max-Min);
It therefore tells you where the current bar is relative to the cycle. If you want to smooth the indicator, then extend the period and/or reduce the polynomial degree.
In code:
NewLength = floor(Period + HilbertWidth+1);
Max = highest(Series,NewLength);
Min = lowest(Series,NewLength);
if Max>Min then
Note that the variable NewLength includes the lag that comes from the hilbert transform, (HilbertWidth=7 by default).
Conclusion:
This is an example of what can be done by combining Legendre polynomials and analytic signals to determine a smooth period without adding time lag.
________________________________
Changes in this one : instead of using true/false options for every single way to display, use Typeparameter as following :nice!
This is some high quality work Mladen.