i-regr指标可以做任意的多项式回归,达到任何程度。我从来没有尝试过高于3度的东西,但代码就在那里,你可以看一看。6度可能会杀死你的CPU,但你可以试一试。
i-regr指标可以做任意的多项式回归,达到任何程度。我从来没有尝试过高于3度的东西,但代码就在那里,你可以看一看。6度可能会杀死你的CPU,但你可以试一试。
谢谢rocketman!完全没有杀死我的CPU - 我将用这个工作一段时间,看看我想出了什么办法。
更新。
i-regr似乎没有很高的准确度--可能是由于高斯(i-regr)和最小二乘法(excel)用于解决。我不知道--还在找,谁有更好的聚能程序?
嗨,dennisj2。
你确定你真的需要你的公式吗?
也许你可以先搜索一下其他的滤波器,比如Kalman, Ehlers, Gauss, Jurik (JMA), DEMA。它们中的大多数都是从低通(物理)频率滤波器派生出来的,而且它们中的大多数都在mt4代码中找到了自己的方法。
也许一个周期较长的JMA(有许多变化)可以满足你的要求?
现在我的探索开始了。
现在,我确定了一个实际应用,我寻求学习(或者,在我的情况下,重新学习)多头趋势线公式背后的数学。祝你好运。最小二乘法的还原和矩阵,加上极其复杂的公式和多项式方程所需的系数计算,(对我来说)要翻译成代码太难了。因此,我想最简单的方法是调用Excel(很可能来自c++),提供一个(x,y)数据值的数组,使用LINEST()计算聚(x,y)截距(趋势线值),并将此值返回到我的桌面应用程序(一个封闭的专有软件应用程序,调用功能有限)。
使用LINEST()组装公式已经成为一个巨大的障碍。提供数据很容易--但是,我怎样才能计算出图形上完美显示的(x,y)截距?每一个新的措施都会改变公式并使用新计算的系数?为什么会出现这种情况?我已经花了好几个小时,在互联网上寻找解决方案--(就像一个男人)最后决定向别人请教。
我已经得到了源值(多年来的源值)。我缺少的是a)生成poly(x,y)截距的方法,b)通过外部调用Excel,c)根据提供的(x,y)数据返回poly(x,y)。
如果谁有关于这个问题的文章或非常具体的处理方法,或者甚至愿意伸出援手,我将永远感激你。
dj
外面有很多关于代数的文章,有希腊语的例子,但实际上是巫术。
例如,维基百科上有一篇关于线性回归 的文章,对我来说完全没有意义,但我现在就可以对你的直线进行线性回归的编码,因为在别的地方我学会了使用这个公式
y=a+bx
然而在维基百科的文章中根本没有提到这个公式,这怎么可能有意义?
我在使用该公式时还了解到
a==斜率
b==截距
计算斜率和截距的数学方法是众所周知的,而且是非常简单的计算数值之和,对其中一些数值进行平方计算等。
我还知道二次回归(二度)的公式是y=ax^2+bx+c。
所以我认为它们是相关的,这应该意味着三度回归的公式是
y=ax^3 + bx^2 + cx + d
所以我认为第6次回归应该是
y=ax^6 + bx^5 + cx^4 + dx^3 + ex^2 + fx + g
但如果a是斜率,b是截距,那么c是什么,d是什么等等?这就是我不能给你的线条编码的唯一原因,我不知道系数是什么,也不知道如何计算它们。
更新:好吧,我又学到了一些东西,现在让我很困惑。
在另一篇文章中,二次多项式被描述为
ax^2 + bx + c = 0
这是否意味着我们根本不需要知道斜率截距的计算方法,我们可以通过求解二次方程来找到a、b和c的值?
但是,ax^2 + bx + c = 0是什么意思?
与
y=ax^2 + bx + c ?
它们看起来很相似,但为什么一个是y=,另一个是=0?
SDC。
一个点的斜率可以通过一个函数 的第一次推导来计算。
像y=ax+b这样的线性函数在任何一点都有相同的斜率:a。
一般来说,线性函数ax^n + bx^n-1 + ...+ z = y 简单来说就是:nax^(n-1) + (n-1)bx^n-2 ... = y'--原函数的最后一个常数变成了0,总是这样!所以ax + b = y =>
所以ax + b = y => y' = a ( <= 1*a^(1-1); b=0 ),二次函数变成y' = 2ax + b ( <= 2ax^(2-1) + 1bx^(1-1); c=0 ) 。
但我认为要理解过滤器的概念,你最好思考(和阅读)一下过滤频率的问题。不管是声音、图片、引文还是...。
人们总是想摆脱噪音--一般来说--短期的频率。而使用线性函数只是一种方法。
SDC:
外面有很多关于代数的文章,有希腊语的例子,但实际上它是巫术。
SDC--你现在和我处于同一水平--我发现的线性回归公式是有效的--我发现有两个明显不同的公式,产生的结果是一样的。如果线性回归(一条直的趋势线)是我们所追求的,那么这些公式就很好。
首先,一些参考材料。
微软:http://office.microsoft.com/en-us/excel-help/linest-HP005209155.aspx
IntegralCalc:https://www.youtube.com/watch?v=1pawL_5QYxE&noredirect=1
给出线性回归方程y=mx+b。
其中y=价格,(例如,Close[x])。
和x=指数(例如,Bar[x])。
m = 斜率(应用于每个(x,y)对的系数)。
和b = Y-截距(应用于每个(x,y)对的Y-截距的基值)
方法A:来自IntegralCalc方法B:来自微软(其中x(overbar)和y(overbar)是平均值)。
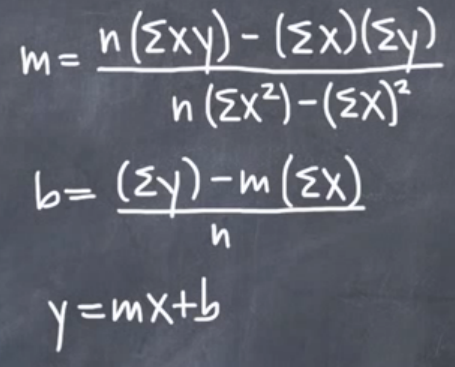
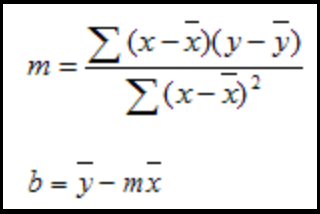
即使是多项式回归趋势线公式的n次方,应用起来也相对容易。
给出公式:y = m1*x1 + m2*x2 + m3*x3 + ...+ b
其中变量x、y、m和b带有线性方程中描述的相同定义。
似乎我什么都有了,那么还缺什么呢?
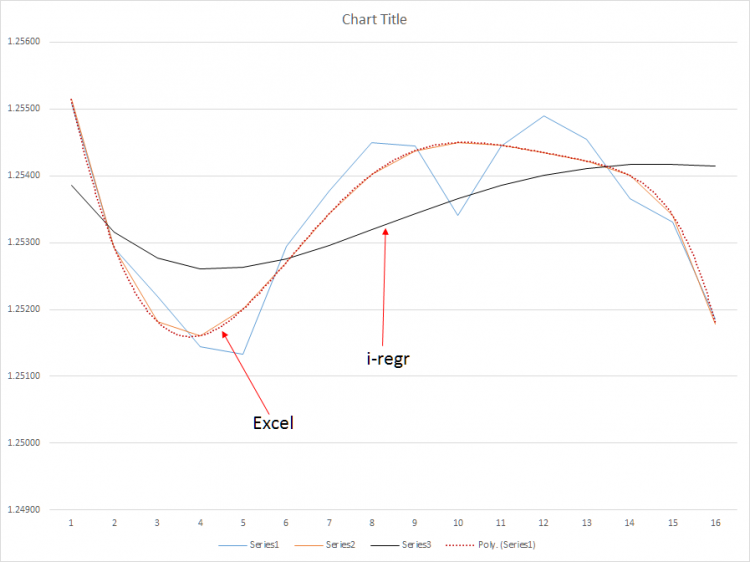
缺少的是对多项式回归的m(斜率)和b(Y截距)的计算;计算这些数值的线性方程不适用于多项式回归。根据我所学到的知识,多项式回归需要一个公式,根据使用矩阵的多项式方程系统来计算最小二乘法。请看上面的例子图。在第一张图中,poly(6)线绝对是无懈可击的--顶部和底部被清楚地叫出来。有了这些数据,我将能够比今天更长时间地持有交易,最终使我每笔交易的平均点数翻倍,甚至可能翻三倍。
在第二张图中,我展示了poly(6)与i-regr方法的结果,该方法使用高斯矩阵来解决斜率系数--不用说,由于该方法的大量延迟,它相当无用。另一方面,简单的移动平均线甚至更糟--在中间市场修正期间,SMA太敏感了,可能会导致我的EA反应过度。
我愿意花钱请人开发一个真正的多项式回归指标--但是,其结果绝对要反映出Excel产生的结果。LINEST()函数是一个黑匣子,其中有许多巫术被用来计算系数。很简单,我需要了解这些巫术。
更新:我附上了一个文件,显示在Excel中实现的方法。
i-regr是根据每个条形的Close[]值工作的,这可能会造成差异(我猜你已经在MT4和excel中平衡了模式长度)。
你可以通过将Close[]改为Open/High/Low或任何其他分析表达式(如权重函数)来轻松改变这一点。
然而,我不相信你能从中获利,它就像任何其他重新绘制的趋势指标一样。
Grazi -
我使用了i-regr并比较了上述结果--Poly(6)算法与i-regr的对比显示,基于相同的数据集,i-regr的延迟大大高于poly(6)--在这个市场上,延迟就是死亡。我的EA不交易日内震荡,而是为趋势而持有。所以,你错了--我确实从我的EA中获利,而且,如果有一个反应较慢的指标,我的EA会比现在捕获更多的市场。具体来说,一旦我整合了一个真正的poly(6)算法,我将有能力更长时间地持有未结头寸,并提前 3-4个时期预测趋势变化,提高 我的进入点。