赫斯特指数 - 页 37 1...303132333435363738394041424344...46 新评论 Dersu 2013.02.23 15:23 #361 你为什么要走这么远?我宁愿和普通火鸡打交道...... Alexey Subbotin 2013.02.23 15:44 #362 faa1947:我总是试图在我的TC中找到最佳的窗口宽度。它在30-70个观测值之间变化(对于H1)。 究竟是什么类型的窗户?例如,与普通的长方形相比,高斯的边界效应 抑制得非常明显(它在频域中也将是高斯的,即它将提供每八度的-40分贝,没有任何侧面的最大值)。然后可以通过考虑更多的信号值来实现同样的反应性。 Alexey Subbotin 2013.02.23 15:45 #363 Dersu:为什么走这么远?我宁愿和普通火鸡打交道...... 那是谁?) Dersu 2013.02.23 15:47 #364 私人德苏! Alexey Subbotin 2013.02.23 15:58 #365 Dersu: 私人德苏! 放心吧!这些信封是什么,红色和绿色? Dersu 2013.02.23 16:00 #366 信封作为信封。已插入。 Alexey Subbotin 2013.02.23 16:13 #367 庆祝活动? Dersu 2013.02.23 16:18 #368 星期六,假日...脱离主题? Vasiliy Sokolov 2013.02.24 10:39 #369 faa1947:如果我们看 "H更具有外部环境的特征",我们应该注意与赫斯特有关的英语术语。这里是BP专著中的一个复制粘贴。一些时间序列 在高滞后期 表现出 明显的关联性,它们被称为称为长内存进程。长记忆是许多地球物理学的一个特点。时间序列。尼罗河的流量在高滞后期有关联性。和Hurst(1951)证明,这影响了最佳设计能力的大坝。Mudelsee(2007)表明,长记忆是一种水文学特性导致长期干旱或极端天气的时间集聚。洪水。在一个相当不同的规模,Leland等人。(1993)发现,以太网局域网(LAN)流量似乎是一个统计学上的自相似性和一个统计学上的自相似性。长记忆过程。他们表明,在这种情况下产生的拥堵的性质是自相似的流量与流量模型预测的流量有很大的不同当时使用的。曼德布罗特和他的同事们研究了以下关系在自相似性和长期记忆之间发挥了主导作用。确立分形几何作为一个研究对象。请注意这些话一些时间序列在高滞后期表现出明显的关联性И显示,长内存我试图找出:什么是长记忆?结果是40多个观测值的自相关!。但在引文中,如此长的一个符号的相关性是极其罕见的。无论如何,花了一个小时后,我没有找到它。大量的人试图使用赫斯特指数。我没有一次看到积极的结果。也许我们应该首先找到cotiers。在哪个长的记忆? 你可以在任何引文中识别这种长记忆。但ACF在这里并不适合。 彼得斯对长期记忆给出了一个有趣的定义。阅读它。在他关于这个问题的书中有很多有趣的信息。据他说,这种过程不能用微不足道的ACF来衡量。ACF在5-6个滞后的范围内工作,仅此而已。如果H表示为一个移动的粒子,其扩散等于距离的平方根,那么我们得到一个正态分布的特例 StdDev = Sqrt(T) = T^(0.5) 。现在,如果粒子的散射略高于或低于0.5,在一种情况下 是可能的,而且只有一种情况:粒子必须记住它过去的状态,因此这样的过程将拥有记忆。也就是说,H不是外部行动的特征,而是取决于过程的先前状态。而如果逃生轨迹被保留下来,就意味着它取决于以前的数值,可以计算出记忆期。而经常发生的情况是,在所有的计算比例上,斜率角都没有变化,同时,它不 等于0.5。在这种情况下,该进程被说成是具有无限内存的真正的赫斯特进程。除了ACF不会显示任何类似的东西。 СанСаныч Фоменко 2013.02.24 11:23 #370 C-4: 你可以在任何引文中识别这种非常长的记忆。但ACF在这里并不适合。 彼得斯对长期记忆给出了一个有趣的定义。阅读它。他的书中有很多关于这个问题的有趣内容。据他说,这种过程不能用微不足道的ACF来衡量。ACF在5-6个滞后的范围内工作,仅此而已。如果H表示为一个移动的粒子,其扩散等于距离的平方根,那么我们得到一个正态分布的特例 StdDev = Sqrt(T) = T^(0.5) 。因此,如果粒子的散射略高于或低于0.5,在一种且仅有一种情况下 是可能的:粒子必须记住其过去的状态,因此这种过程将拥有记忆。也就是说,H不是外部行动的特征,而是取决于过程的先前状态。而如果逃生轨迹被保留下来,就意味着它取决于以前的数值,可以计算出记忆期。而经常发生的情况是,在所有的计算尺度上,斜率角都没有变化,同时,它不 等于0.5。在这种情况下,该进程被说成是具有无限内存的真正的赫斯特进程。除了ACF不会显示任何类似的东西。不幸的是,我对这个问题没有自己的看法。但我可以向你介绍一下这本书Cowpertwait和A.V. Metcalfe,《R的时间序列入门》,159页。使用R,DOI 10.1007/978-0-387-88698-5 8,© Springer Science+Business Media, LLC 2009其中第8章介绍了FARIMA的拟合过程。在这个过程中使用了ACF。附上文本。不幸的是,公式和理论部分并没有结果。但FARIMA的拟合过程有具体描述 附加的文件: long.zip 203 kb 1...303132333435363738394041424344...46 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
你为什么要走这么远?
我宁愿和普通火鸡打交道......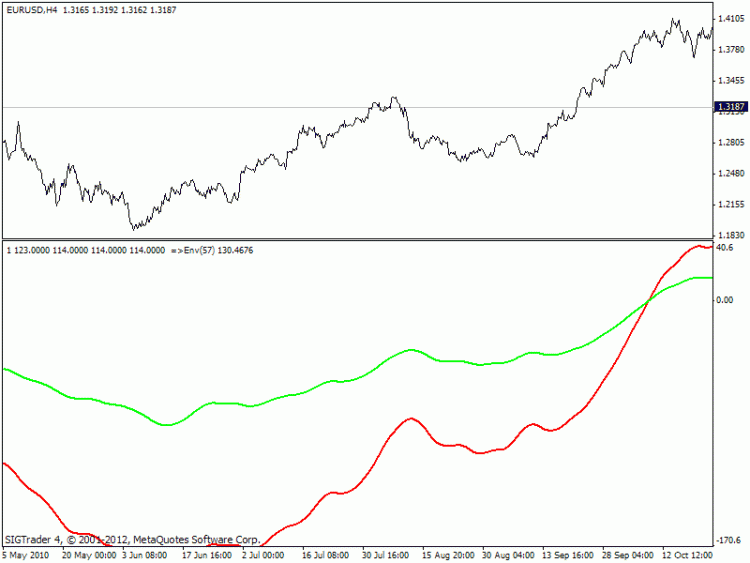
我总是试图在我的TC中找到最佳的窗口宽度。它在30-70个观测值之间变化(对于H1)。
究竟是什么类型的窗户?例如,与普通的长方形相比,高斯的边界效应 抑制得非常明显(它在频域中也将是高斯的,即它将提供每八度的-40分贝,没有任何侧面的最大值)。然后可以通过考虑更多的信号值来实现同样的反应性。
为什么走这么远?
我宁愿和普通火鸡打交道......
那是谁?)
私人德苏!
放心吧!这些信封是什么,红色和绿色?
信封作为信封。
已插入。
星期六,假日...
脱离主题?
如果我们看 "H更具有外部环境的特征",我们应该注意与赫斯特有关的英语术语。这里是BP专著中的一个复制粘贴。
确立分形几何作为一个研究对象。
请注意这些话
一些时间序列在高滞后期表现出明显的关联性
И
显示,长内存
我试图找出:什么是长记忆?结果是40多个观测值的自相关!。但在引文中,如此长的一个符号的相关性是极其罕见的。无论如何,花了一个小时后,我没有找到它。
大量的人试图使用赫斯特指数。我没有一次看到积极的结果。也许我们应该首先找到cotiers。在哪个长的记忆?
彼得斯对长期记忆给出了一个有趣的定义。阅读它。在他关于这个问题的书中有很多有趣的信息。据他说,这种过程不能用微不足道的ACF来衡量。ACF在5-6个滞后的范围内工作,仅此而已。如果H表示为一个移动的粒子,其扩散等于距离的平方根,那么我们得到一个正态分布的特例 StdDev = Sqrt(T) = T^(0.5) 。现在,如果粒子的散射略高于或低于0.5,在一种情况下 是可能的,而且只有一种情况:粒子必须记住它过去的状态,因此这样的过程将拥有记忆。也就是说,H不是外部行动的特征,而是取决于过程的先前状态。而如果逃生轨迹被保留下来,就意味着它取决于以前的数值,可以计算出记忆期。而经常发生的情况是,在所有的计算比例上,斜率角都没有变化,同时,它不 等于0.5。在这种情况下,该进程被说成是具有无限内存的真正的赫斯特进程。除了ACF不会显示任何类似的东西。
你可以在任何引文中识别这种非常长的记忆。但ACF在这里并不适合。
彼得斯对长期记忆给出了一个有趣的定义。阅读它。他的书中有很多关于这个问题的有趣内容。据他说,这种过程不能用微不足道的ACF来衡量。ACF在5-6个滞后的范围内工作,仅此而已。如果H表示为一个移动的粒子,其扩散等于距离的平方根,那么我们得到一个正态分布的特例 StdDev = Sqrt(T) = T^(0.5) 。因此,如果粒子的散射略高于或低于0.5,在一种且仅有一种情况下 是可能的:粒子必须记住其过去的状态,因此这种过程将拥有记忆。也就是说,H不是外部行动的特征,而是取决于过程的先前状态。而如果逃生轨迹被保留下来,就意味着它取决于以前的数值,可以计算出记忆期。而经常发生的情况是,在所有的计算尺度上,斜率角都没有变化,同时,它不 等于0.5。在这种情况下,该进程被说成是具有无限内存的真正的赫斯特进程。除了ACF不会显示任何类似的东西。
不幸的是,我对这个问题没有自己的看法。
但我可以向你介绍一下这本书
Cowpertwait和A.V. Metcalfe,《R的时间序列入门》,159页。
使用R,DOI 10.1007/978-0-387-88698-5 8,
© Springer Science+Business Media, LLC 2009
其中第8章介绍了FARIMA的拟合过程。在这个过程中使用了ACF。
附上文本。不幸的是,公式和理论部分并没有结果。
但FARIMA的拟合过程有具体描述