差分微积分,例子。 - 页 6 12345678910111213...24 新评论 Aleksey Panfilov 2018.01.18 08:59 #51 用四度多项式进行平均,杠杆率为72(四度EMA),用立方抛物线(三度多项式)推算出不同的杠杆率。 a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975; a5_Buffer[i+92]=a1_Buffer[i]; if(i<=1100) { for(z=92-1;z>=0;z--){ a5_Buffer[i+0+z]= 4*a5_Buffer[i+1+z] - 6*a5_Buffer[i+2+z] + 4*a5_Buffer[i+3+z] - 1*a5_Buffer[i+4+z]; }} a2_Buffer[i+20]=a5_Buffer[i+20]; a3_Buffer[i+38]=a5_Buffer[i+38]; a4_Buffer[i+56]=a5_Buffer[i+56]; a6_Buffer[i+74]=a5_Buffer[i+74]; 第一个图是一个绘图方案,在第二个图中,所有没有重画 的线都画到最后一个值。地下室中的指标只在设定的线偏移量上有所不同。 附加的文件: 2018_01_18_EMA_Polynom_s4_s3_p72_6v.1p.mq4 17 kb 2018_01_18_EMA_Polynom_s4_s3_p72_9v.21.mq4 17 kb Aleksey Panfilov 2018.01.18 09:06 #52 用四度多项式进行平均,杠杆率为72(四度EMA),用四度多项式外推到不同的杠杆 率。 a1_Buffer[i]=((open[i] - Znach) +5061600*a1_Buffer[i+1 ]-7489800 *a1_Buffer[i+2 ]+4926624*a1_Buffer[i+3 ]-1215450*a1_Buffer[i+4 ])/1282975; a5_Buffer[i+92]=a1_Buffer[i]; if(i<=1100) { for(z=92-1;z>=0;z--){ a5_Buffer[i+0+z]= 5*a5_Buffer[i+1+z] - 10*a5_Buffer[i+2+z] + 10*a5_Buffer[i+3+z] - 5*a5_Buffer[i+4+z] + 1*a5_Buffer[i+5+z]; }} a2_Buffer[i+20]=a5_Buffer[i+20]; a3_Buffer[i+38]=a5_Buffer[i+38]; a4_Buffer[i+56]=a5_Buffer[i+56]; a6_Buffer[i+74]=a5_Buffer[i+74]; 第一个图是一个绘图方案,在第二个图中,所有没有重画 的线都画到最后一个值。地下室中的指标只在设定的线偏移量上有所不同。 附加的文件: 2018_01_18_EMA_Polynom_s4_s4_p72_2v.1t.mq4 17 kb 2018_01_18_EMA_Polynom_s4_s4_p72_8v.2w.mq4 17 kb Nikolai Semko 2018.01.18 15:56 #53 阿列克谢,我可以给你一些免费的建议和一个提示。我已经告诉过你,向左转是,怎么说呢?- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。 但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。 Aleksey Panfilov 2018.01.18 18:31 #54 尼古拉-森科。阿列克谢,我可以给你免费的建议和一个提示。我已经说过,向左移动是,我怎么说呢?- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。 但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。是的,尼古拉,我完全同意你的观点,当然,每个导数都会使正弦图向左移动四分之一个周期。因此,在进行比较时,我消除了人为的线路转移。这可以从过去几个帖子中的第二个数字 看出。除了灰色的细线外,所有的线都是在最后一个条形图上画出来的,不会重画。而图表中的一些向左移动是由于推断。 而这些线条确实仍然可以被区分,在我们的案例中,去除第一个和/或第二个差异,这是在原型。:)))向左移动是为了把所有的线包括施工线连接成一个整体,并看到整体方案。 Nikolai Semko 2018.01.18 19:00 #55 阿列克谢-潘菲洛夫。是的,尼古拉,我完全同意你的观点,当然每个导数都会使正弦图向左移动四分之一个周期。这就是为什么在进行比较时,我消除了人为的线路转移。这可以从过去几个帖子中的第二个数字 看出。除了灰色的细线外,所有的线都是在最后一个条形图上画的,并没有重画。而图表中的一些向左移动是由于推断。向左移位是为了将所有的线条,包括施工线,连接到整个画面中,并展示总体方案。上面的图表可以忽略,因为它被移到了左边,尾部被重新绘制。而下面那个看起来很滞后,很平凡。这一切大惊小怪的意义何在? Aleksey Panfilov 2018.01.18 19:06 #56 尼古拉-森科。 上图可以忽略不计,因为它是向左移动的,而且尾部是透支的。而下面那个看起来很滞后,很平凡。那么这些大惊小怪的事情有什么意义呢?))))我们会 "边走边看"。到目前为止,一切都在轨道上。)) Nikolai Semko 2018.01.18 22:58 #57 尼古拉-森科。阿列克谢,我可以给你免费的建议和一个提示。我已经说过,向左转是,怎么说呢......我应该温和地说说。- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。 但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。下面是这种方法的一个可能的实施。没有重画和移位。 这是你的线的二阶导数。 附加的文件: Banzai.mq4 5 kb Banzai.mq5 6 kb Nikolai Semko 2018.01.18 23:36 #58 有时甚至是非常相关的,不滞后的 Maxim Kuznetsov 2018.01.19 01:09 #59 尼古拉-森科。阿列克谢,我可以给你一些免费的建议和一个提示。我已经说过,向左应用移位是,怎么说呢,很温和地...-一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。 但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。我今天心情很好。Alg. on "shift left" (what a name for it :) ) 。1)得到两个SMA,一个快,一个慢。2.向左移一个半周期(各为其主)。3.我们惊讶地看到,:3.0的波形在彼此之间旋转。3.1.快者在极点之前(有时更早)将慢者向上移动。3.2. "成对的 "交叉点(在极值之前向上,在极值之后向下)。4.将条形图移回实时,但(与n2不同)是相同的数量。一个将在0处结束,另一个将强烈地向右走。 5.现在看到了过去极值和以前的交叉点,我们将看看它已经交叉的地方。根据什么,我们可以过滤掉明显的假阳性,做出相当不错的条目。 Nikolai Semko 2018.01.19 02:19 #60 Maxim Kuznetsov:我今天心情很好Alg.在 "左移 "上(这名字真好听)。1.我们根据经典的方法,采取两条均线,一条快线和一条慢线。2.向左移一个半周期(各为其主)。3.我们惊讶地看到,:3.0的波形在彼此之间旋转。3.1.快者在极点之前(有时更早)将慢者向上移动。3.2. "成对的 "交叉点(在极值之前向上,在极值之后向下)。4.将条形图移回实时,但(与n2不同)是相同的数量。一个将在0处结束,另一个将强烈地向右走出去。 5.现在看到了过去极值和以前的交叉点,我们将看看它已经交叉的地方。根据什么,我们可以消除明显的假阳性,做出相当不错的条目。也许,这里面有什么东西。但它不是一个左移算法,而是一个右移算法。 12345678910111213...24 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
用四度多项式进行平均,杠杆率为72(四度EMA),用立方抛物线(三度多项式)推算出不同的杠杆率。
第一个图是一个绘图方案,在第二个图中,所有没有重画 的线都画到最后一个值。
地下室中的指标只在设定的线偏移量上有所不同。
用四度多项式进行平均,杠杆率为72(四度EMA),用四度多项式外推到不同的杠杆 率。
第一个图是一个绘图方案,在第二个图中,所有没有重画 的线都画到最后一个值。
地下室中的指标只在设定的线偏移量上有所不同。
阿列克谢,我可以给你一些免费的建议和一个提示。
我已经告诉过你,向左转是,怎么说呢?- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。
但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。
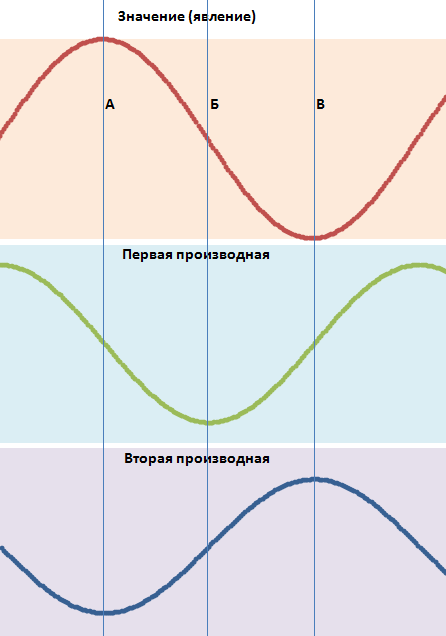
例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。
阿列克谢,我可以给你免费的建议和一个提示。
我已经说过,向左移动是,我怎么说呢?- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。
但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。
例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。
是的,尼古拉,我完全同意你的观点,当然,每个导数都会使正弦图向左移动四分之一个周期。
因此,在进行比较时,我消除了人为的线路转移。这可以从过去几个帖子中的第二个数字 看出。除了灰色的细线外,所有的线都是在最后一个条形图上画出来的,不会重画。而图表中的一些向左移动是由于推断。
而这些线条确实仍然可以被区分,在我们的案例中,去除第一个和/或第二个差异,这是在原型。:)))
向左移动是为了把所有的线包括施工线连接成一个整体,并看到整体方案。
是的,尼古拉,我完全同意你的观点,当然每个导数都会使正弦图向左移动四分之一个周期。
这就是为什么在进行比较时,我消除了人为的线路转移。这可以从过去几个帖子中的第二个数字 看出。除了灰色的细线外,所有的线都是在最后一个条形图上画的,并没有重画。而图表中的一些向左移动是由于推断。
向左移位是为了将所有的线条,包括施工线,连接到整个画面中,并展示总体方案。
上面的图表可以忽略,因为它被移到了左边,尾部被重新绘制。而下面那个看起来很滞后,很平凡。这一切大惊小怪的意义何在?
上图可以忽略不计,因为它是向左移动的,而且尾部是透支的。而下面那个看起来很滞后,很平凡。那么这些大惊小怪的事情有什么意义呢?
))))
我们会 "边走边看"。
到目前为止,一切都在轨道上。))
阿列克谢,我可以给你免费的建议和一个提示。
我已经说过,向左转是,怎么说呢......我应该温和地说说。- 是一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。
但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。
例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。
下面是这种方法的一个可能的实施。没有重画和移位。 这是你的线的二阶导数。
有时甚至是非常相关的,不滞后的
阿列克谢,我可以给你一些免费的建议和一个提示。
我已经说过,向左应用移位是,怎么说呢,很温和地...-一项艰巨的任务。你只会得到那些观看你的线程的人的咒骂。顺便说一句,这也是你在自己的主题中为自己的孤独感到自豪的原因之一。
但如果要 把有一个拐点的周期线向左移动 半个波段(或者说如果在局部最低点和最高点之间只有一个拐点)而不进行实际移动,你可以使用该函数的导数。的确,这不是一个实际的转变,但在本质上。一个函数的导数是与直线相切的角度。计算方法很简单:buf[i]-buf[i+1]。
例如,这里有一个正弦波的第一和第二导数。函数本身的拐点成为其导数的局部最大值和最小值。
我今天心情很好。
Alg. on "shift left" (what a name for it :) ) 。
1)得到两个SMA,一个快,一个慢。
2.向左移一个半周期(各为其主)。
3.我们惊讶地看到,:
3.0的波形在彼此之间旋转。
3.1.快者在极点之前(有时更早)将慢者向上移动。
3.2. "成对的 "交叉点(在极值之前向上,在极值之后向下)。
4.将条形图移回实时,但(与n2不同)是相同的数量。一个将在0处结束,另一个将强烈地向右走。
5.现在看到了过去极值和以前的交叉点,我们将看看它已经交叉的地方。根据什么,我们可以过滤掉明显的假阳性,做出相当不错的条目。
我今天心情很好
Alg.在 "左移 "上(这名字真好听)。
1.我们根据经典的方法,采取两条均线,一条快线和一条慢线。
2.向左移一个半周期(各为其主)。
3.我们惊讶地看到,:
3.0的波形在彼此之间旋转。
3.1.快者在极点之前(有时更早)将慢者向上移动。
3.2. "成对的 "交叉点(在极值之前向上,在极值之后向下)。
4.将条形图移回实时,但(与n2不同)是相同的数量。一个将在0处结束,另一个将强烈地向右走出去。
5.现在看到了过去极值和以前的交叉点,我们将看看它已经交叉的地方。根据什么,我们可以消除明显的假阳性,做出相当不错的条目。
也许,这里面有什么东西。但它不是一个左移算法,而是一个右移算法。