В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
这并不矛盾。供求基本规律预示了这些效应。问题是:整个模型应该动态地考虑,即水平基本通道的边界会随着时间的推移而变化。为了理解我的意思,有必要首先考虑一个经典的静态供需模型(针对 "此时此地"):
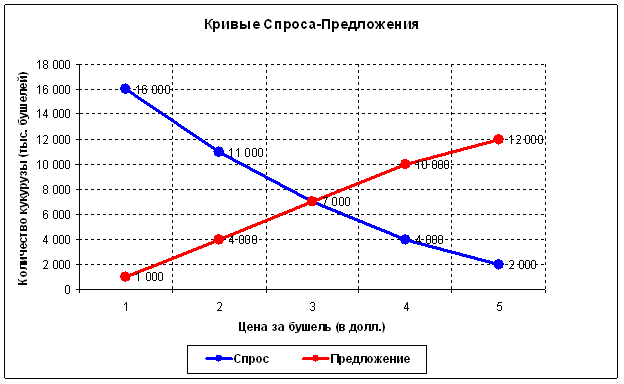
也就是说,在每个时间点上,只有一个最大效率的商品交换点(在本例中为 7000 蒲式耳,价格为 3 美元)。在所有其他时间点上,用较少的货币兑换较少的商品。宏观经济形势在不断变化,这意味着这个有效交换点本身也在变化。然而,市场是有效的,它的主要任务就是不断寻找这样一个点或非常均衡的价格("所有想买的人都买了,所有想卖的人都卖了")。此时的交易量 应该很大,因为此时的商品交换量最大。市场需要时间来 实现这样的交易量。这一理论预测了交易量积累的效果:
市场大部分时间处于盘整阶段(处于最高效率区域)。
然而,世界经济 作为一个整体在不断发展。新技术不断涌现,生活水平不断提高。因此,一方面,人们需要越来越多的商品和服务,另一方面,科技进步使得生产越来越多的商品和服务成为可能。流动性随着时间的推移而增加。世界市场的容量必然增加,其波动性也随之增加,从而导致危机规模的崩溃。随着时间的推移,需求增加,价格上涨。与此同时,科技进步为这种需求提供了越来越多的商品和服务。因此,随着时间的推移,均衡点一般会向上和向右移动。市场在这一点上不断徘徊,一般也会增长(趋于高价)。

这就是 "趋势效应 "的来源。通过数学计算,这一切都非常完美,简直令人叹为观止。无论如何,经济效应应该解释数学依赖性,而不是相反。
文章中有一处不准确的地方,如果我们以醉酒的水手作为类比,那么台阶的大小是不同的。粗略地说,如果从酒馆出发,1 步的长度是 80 厘米,返回(到酒馆)一步的长度是 60 厘米。趋势是一样的,众所周知,市场向下运动的速度快于向上运动的速度。而在这篇文章中,所有的步数都是一样的+1 或-1。
因此,这个模型并不充分。它只是一枚硬币,其分布特性早已为人所知,并被研究了很久。
这篇文章有一个不准确的地方,如果我们以醉酒的水手作为类比,那么台阶的大小是不同的。粗略地说,如果从酒馆出发,1 步的长度是 80 厘米,退一步(到酒馆)是 60 厘米。趋势是一样的,众所周知,市场向下运动的速度快于向上运动的速度。在这篇文章中,所有的步骤都是相同的+1 或-1"。
硬币有一个连续的类似物--几何布朗运动模型。这里介绍的是 http://algoritmus.ru/?p=2889。
"解决算法交易问题的随机方法"。
作者: 阿尔森-雅科夫列夫、格里戈里-弗兰古里迪
发表于:《D-Shtrich》杂志 2010 年 9 月第 16/6 期
这篇文章的观点与我的文章相同,只是多了一些数学知识。采用离散模型还是连续模型是一个品味问题。它们是一样的。只是一个模型有积分,另一个模型有和。硬币模型已经为小学生所理解,而连续模型只有学生才能理解。
"众所周知,市场向下运动的速度快于向上运动的速度"--这对我来说非常有趣--您能给我一个研究/文章的链接吗--我需要它来进行自我教育。
"因此,无论如何都不能认为这个模型是适当的。它只是一枚硬币,其分布特性早已为人所知并被研究过"。- 没有任何模型能百分之百地充分描述现实。包括作为市场模型的硬币汇率。这就是为什么我们不得不发明一个带有趋势的硬币模型,以便更充分地适应市场。
- 2010.09.13
- val
- algoritmus.ru
图 2 中的黄色曲线是最接近平坦的曲线。如果取参数 a=-0.5,就会得到最接近平面的曲线。那么我们将得到一条水平线+1 -1 +1 -1 -1 +1 -1 ..... 因此,硬币的两面足以描述一个平面。顺便说一下,文章中的 "平 "被称为 "反趋势"。
但这样一来,整个图表就会变得更加水平,如果我的理解没错的话。在真实市场中,既可能有急剧的趋势,也可能有坚硬的平坦,也就是说,这些现象是独立的。独立性就是需要硬币的第三面。简单地说,市场在平面上徘徊,是因为时间因素在徘徊,而硬币有一个一维的徘徊模型,简单地(没有徘徊)扫一下这个模型的时间是不太正确的。不过,尽管这篇文章非常有用。
完全正确,在有趋势的硬币模型中,趋势性被认为在市场的整个生命周期中都是不变的。而正如实际汇率的趋势性指标所示,趋势性是不断变化的。只有在长期(数年)的平均值中,趋势性才会被视为常数。
为了使 "带趋势的硬币汇率 "模型与市场相对应,可以将其复杂化。参数 "a "可以随机地与时间相关,也可以发明其他参数。这是很有创意的事情。严格来说,没有必要引入第二个维度,但如果你想的话,可以在 "a "旁边添加第二个混沌乘数。
需要一个简单的恒定趋势模型来测试这个指标,例如,新移动迷你最大值技术分析指标及其在 MQL5 中的实现。 在实际过程中处理这样一个指标是不现实的,但在一个简单的恒定趋势模型上测试它将是一件好事。
......采用离散模型还是连续模型是一个品味问题。它们是一样的。只是一个模型有积分,另一个有和。硬币模型已经为小学生所理解,而连续模型只有学生才懂......
这就是错误所在。
1.必须正确地从连续模型过渡到离散模型。
2. 两个模型可以相同(连续和离散),但必须满足一个条件,即 "+"和"-"的步长必须相同。其大小。
3. 通过条形图分析,您的说法 "它们是相同的 "是正确的。证明所有条形图都是一样的。你能证明吗?
4. 只有一种图表具有这种特性,即 Renko 图表......您可以用 +1 -1(https://www.mql5.com/zh/code/9447#25419) 代替它。
感谢您的文章链接。我已经读过了。它建议使用 ARFIMA 模型,即随机漫步模型。这些是不同的模型。如果能读一下下面这篇文章,你和作者的文章都会很有意思。这篇文章证明了你们提出的市场模型是充分的。不只是用文字断言,而是用数学证明......并给出了这个数字的计算方法......
H.Y. 只是很多人都掌握了 "充分性 "这个美丽的词,但如何计算却连自己都不知道。您在帖子中写道,100% 充分的模型是不存在的。我完全同意您的观点。问题是,所提出的模型有多少是符合市场的,20%、30%还是99.999999999%....。
试着建立一个堆栈模型,该堆栈有一个清晰的结构,堆栈会看到上下一定数量点的命令。
生成器通过所有单元格(可以不是 +1 -1 而是生成随机量),然后在生成器通过堆栈的所有单元格后,计算堆栈中间点的移动位置。
生成 32768 个兰特后,不要忘记重新启动 SRAND,否则序列将重复。
新文章 随机游走和趋势指标已发布:
随机游走和实际的市场数据看起来非常类似,但是它有一些重要的特征。在本文中,我们将通过用掷硬币游戏进行模拟,讨论随机游走的特性。为了研究数据的特性,开发了趋势指标。
作者:Гребенев Вячеслав