Discussão do artigo "Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 11): Paredes numéricas"
Você pode verificar essa tabela?
Se eu tentar repetir isso, obtenho resultados diferentes:
| Linha 0 | 0 | 0 | 0 | 0 |
| Linha 1 | 1 | 1 | 1 | 1 |
| Linha 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Linha 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
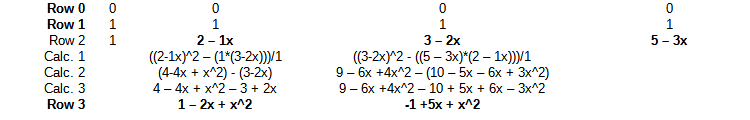
Você pode verificar essa tabela?
Se eu tentar repetir isso, obtenho resultados diferentes:
| Linha 0 | 0 | 0 | 0 | 0 |
| Linha 1 | 1 | 1 | 1 | 1 |
| Linha 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Linha 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
Olá,
Acabei de ver isso. Vou dar uma olhada e reverter.
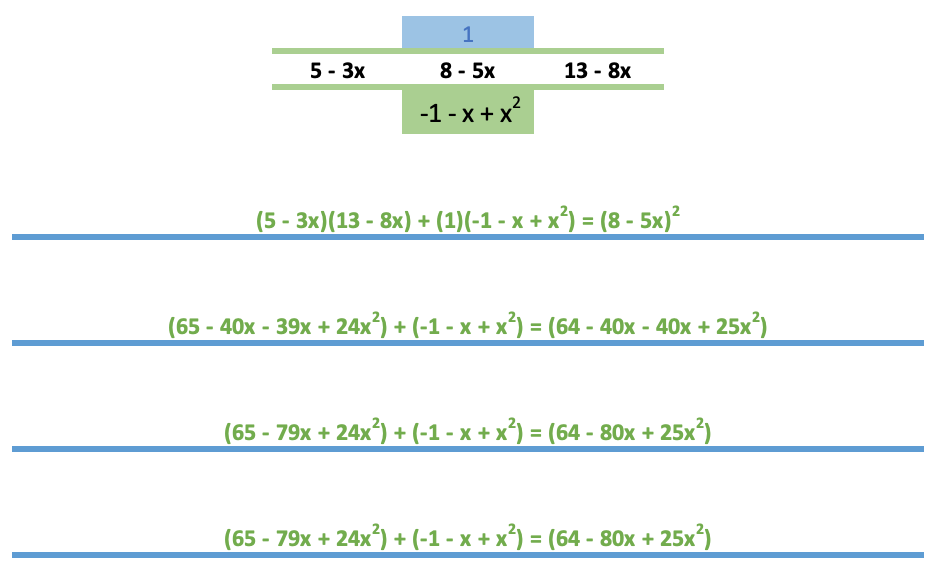
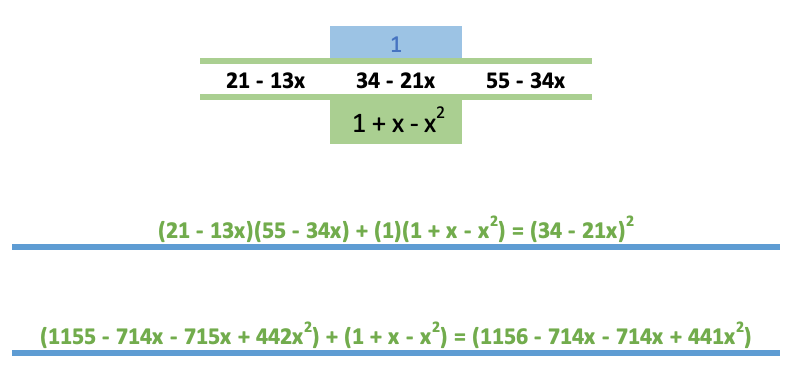
Veja abaixo:
Não é assim que as identidades são provadas, mas acho que a álgebra está correta.
Veja abaixo:
Não é assim que as identidades são provadas, mas acho que a álgebra está correta.
Desculpe, não :(
Parece que seu exemplo é o único que funciona (você realmente precisa desse exemplo?), veja aqui.
| Linha 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Linha 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Linha 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x | 8 - 5x | 13 - 8x | 31 - 13x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | (5 - 3x)^2 - ( (3 - 2x)(8 - 5x)) | (8 - 5x)^2 - (5 - 3x)(13 - 8x) | (13 - 8x)^2 - ( (8 - 5x)(31 - 13x) ) | ||
| Calc. 2 | (4 - 4x + x^2) - (3 - 2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | 25 - 30x + 9x^2 - (24 - 15x +16x + 10x^2) | 64 - 80x +25x^2 - (65 - 39x - 40x + 24x) | 169 - 208x + 64x^2 - (248 - 104x - 155x + 65x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | 25 - 30x + 9x^2 - 24 + 15x - 16x - 10x^2) | 64 - 80x +25x^2 - 65 + 39x + 40x - 24x) | 169 - 208x + 64x^2 - 248 + 104x + 155x - 65x^2) | ||
| Linha 3 | 1 - 2x + x^2 | -1 +5x + x^2 | 1 - 31x - x^2 | -1 - 1x + x^2 | -79 - 51x - 1x^2 |
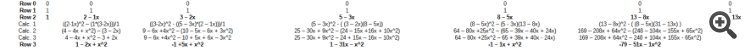
- mathworld.wolfram.com
Gostaria de examinar todos eles, mas você entendeu...
Sim, você está certo, exceto no primeiro cálculo - talvez você o tenha escolhido infelizmente.
Com 1 - 2x + x^2, ele corresponde aos seus resultados alternados de -1 -1x + x^2 e 1 +1x - x^2 :(
Sim, você está certo, exceto no primeiro cálculo - talvez você o tenha escolhido infelizmente.
Com 1 - 2x + x^2, ele corresponde aos seus resultados alternados de -1 -1x + x^2 e 1 +1x - x^2 :(
Hum, você disse que apenas um corresponde, então o que acabei de compartilhar foi um segundo que corresponde.
Eu poderia examinar todos, mas se você seguir meu processo acima, deverá obter resultados semelhantes em todos.
- 2024.01.31
- MetaQuotes
- www.mql5.com
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Funcionalidades do assistente MQL5 que você precisa conhecer (Parte 11): Paredes numéricas foi publicado:
As paredes numéricas (Number Walls) são uma variante do registrador de deslocamento com realimentação linear (Linear Shift Back Registers), que avalia previamente sequências para previsibilidade verificando a convergência. Vamos ver como essas ideias podem ser usadas no MQL5.
Para várias séries temporais, é possível derivar uma fórmula para o próximo valor na sequência com base nos valores anteriores que apareceram nela. As paredes numéricas permitem alcançar isso criando previamente uma "parede de números" na forma de uma matriz usando a chamada regra cruzada (cross-rule). Ao criar esta matriz, o objetivo principal é determinar se a sequência em questão converge. O algoritmo da regra cruzada da parede numérica responde a esta pergunta se, após várias linhas de aplicação, as linhas subsequentes na matriz consistirem apenas em zeros.
No artigo apresentado, que demonstra esses conceitos, a série de Laurent (Laurent Power Series), também conhecida como série formal de Laurent (Formal Laurent Series, FLS), foi usada como base para representar essas sequências com sua aritmética em formato polinomial usando produtos de Cauchy.
Abaixo estão os testes comparativos dos EAs montados com o Assistente. Ambos usam sinais do Awesome Oscillator e têm as mesmas configurações de entrada, conforme mostrado abaixo:
A diferença entre eles é que um EA usa o Parabolic SAR para rastrear e fechar posições abertas, enquanto o outro usa o algoritmo da parede numérica apresentado neste artigo. No entanto, seus relatórios de teste no EURUSD no último ano, em um timeframe de uma hora, apesar de usar o mesmo sinal, diferem.
Autor: Stephen Njuki