Can you please check this table:
If I try to repeat this I get different results:
| Row 0 | 0 | 0 | 0 | 0 |
| Row 1 | 1 | 1 | 1 | 1 |
| Row 2 | 1 | 2 – 1x | 3 – 2x | 5 – 3x |
| Calc. 1 | ((2-1x)^2 – (1*(3-2x)))/1 | ((3-2x)^2 - ((5 – 3x)*(2 – 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 – 6x +4x^2 – (10 – 5x – 6x + 3x^2) | ||
| Calc. 3 | 4 – 4x + x^2 – 3 + 2x | 9 – 6x +4x^2 – 10 + 5x + 6x – 3x^2 | ||
| Row 3 | 1 – 2x + x^2 | -1 +5x + x^2 |
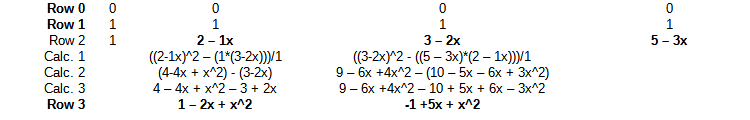
Can you please check this table:
If I try to repeat this I get different results:
| Row 0 | 0 | 0 | 0 | 0 |
| Row 1 | 1 | 1 | 1 | 1 |
| Row 2 | 1 | 2 – 1x | 3 – 2x | 5 – 3x |
| Calc. 1 | ((2-1x)^2 – (1*(3-2x)))/1 | ((3-2x)^2 - ((5 – 3x)*(2 – 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 – 6x +4x^2 – (10 – 5x – 6x + 3x^2) | ||
| Calc. 3 | 4 – 4x + x^2 – 3 + 2x | 9 – 6x +4x^2 – 10 + 5x + 6x – 3x^2 | ||
| Row 3 | 1 – 2x + x^2 | -1 +5x + x^2 |
Hello,
Just seeing this. Let me take a look and revert.
Pse see below:
This is not how identities are proved but I think the algebra is okay.
Sorry no :(
It seems that your example is the only one that works (do you really need this example?), see here.
| Row 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Row 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
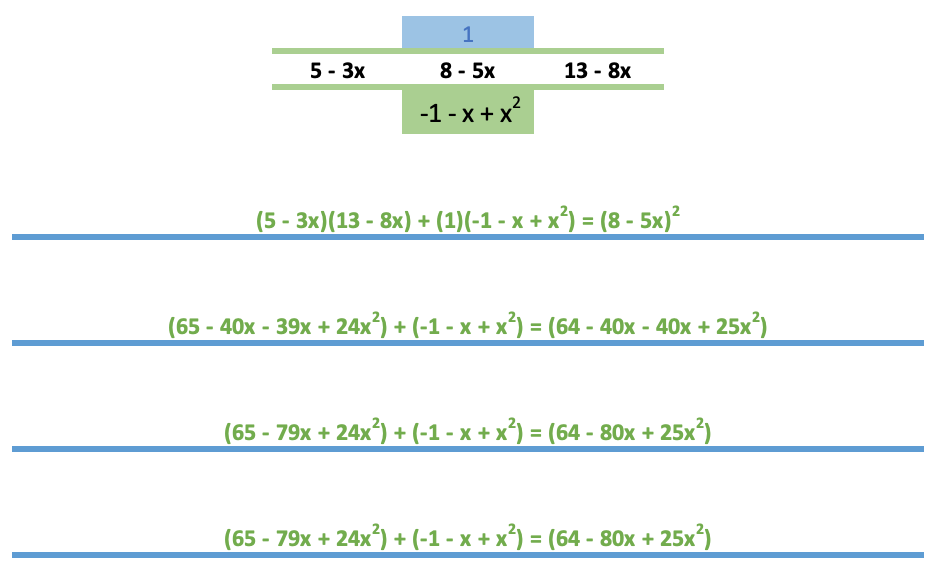
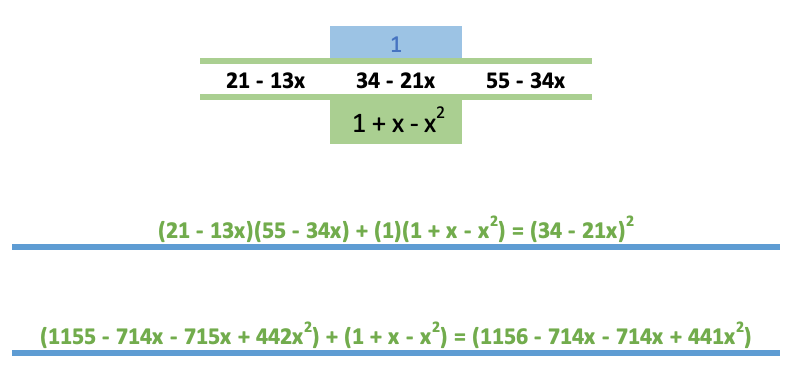
| Row 2 | 1 | 2 – 1x | 3 – 2x | 5 – 3x | 8 – 5x | 13 – 8x | 31 – 13x |
| Calc. 1 | ((2-1x)^2 – (1*(3-2x)))/1 | ((3-2x)^2 - ((5 – 3x)*(2 – 1x)))/1 | (5 – 3x)^2 - ( (3 – 2x)(8 – 5x)) | (8 – 5x)^2 – (5 - 3x)(13 – 8x) | (13 – 8x)^2 - ( (8 – 5x)(31 – 13x) ) | ||
| Calc. 2 | (4 – 4x + x^2) – (3 – 2x) | 9 – 6x +4x^2 – (10 – 5x – 6x + 3x^2) | 25 – 30x + 9x^2 – (24 – 15x +16x + 10x^2) | 64 – 80x +25x^2 – (65 – 39x – 40x + 24x) | 169 – 208x + 64x^2 – (248 – 104x – 155x + 65x^2) | ||
| Calc. 3 | 4 – 4x + x^2 – 3 + 2x | 9 – 6x +4x^2 – 10 + 5x + 6x – 3x^2 | 25 – 30x + 9x^2 – 24 + 15x – 16x – 10x^2) | 64 – 80x +25x^2 – 65 + 39x + 40x - 24x) | 169 – 208x + 64x^2 – 248 + 104x + 155x - 65x^2) | ||
| Row 3 | 1 – 2x + x^2 | -1 +5x + x^2 | 1 – 31x – x^2 | -1 – 1x + x^2 | -79 – 51x – 1x^2 |
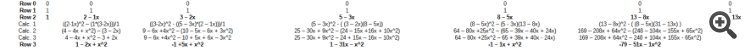
- mathworld.wolfram.com
Yes you are right except the first calculation - maybe you have chosen it unfortunately.
With 1 – 2x + x^2 it does match with your alternating results of -1 -1x + x^2 and 1 +1x – x^2 :(
Yes you are right except the first calculation - maybe you have chosen it unfortunately.
With 1 – 2x + x^2 it does match with your alternating results of -1 -1x + x^2 and 1 +1x – x^2 :(
Um, you said only one matches, so what I just shared was a second one that matches.
I could go through all, but if you follow my process above, you should get similar results on all.

- 2024.01.31
- MetaQuotes
- www.mql5.com
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use

Check out the new article: MQL5 Wizard Techniques you should know (Part 11): Number Walls.
Number Walls are a variant of Linear Shift Back Registers that prescreen sequences for predictability by checking for convergence. We look at how these ideas could be of use in MQL5.
For a few time-series, it is possible to devise a formula for the next value in the sequences basing off of previous values that appeared within it. Number walls allow this to be accomplished by preliminarily generating a ‘wall of numbers’, in the form of a matrix via what is referred to as the cross-rule. In generating this matrix, the primary goal is to establish if the sequence in question is convergent and the number wall cross rule algorithm gladly answers this question, if after a few rows of application, the subsequent rows in the matrix are only zeroes.
In this published paper, that exhibits these concepts, the Laurent Power Series aka Formal Laurent Series (FLS) was used as a framework for representing these sequences with its arithmetic in polynomial format while using Cauchy products.
Comparative tests of wizard assembled expert advisers are shown below. They both use the awesome oscillator signal and in principal have simillar inputs as indicated here:
The difference betwen them is one expert uses the parabolic sar to trail and close open positions while the other uses the number wall algorithm introduced in this article. However their reports when tested on EURUSD over the past year on the hourly time frame, despite the same signal, do differ.
Author: Stephen Njuki