Olá pessoal!
....
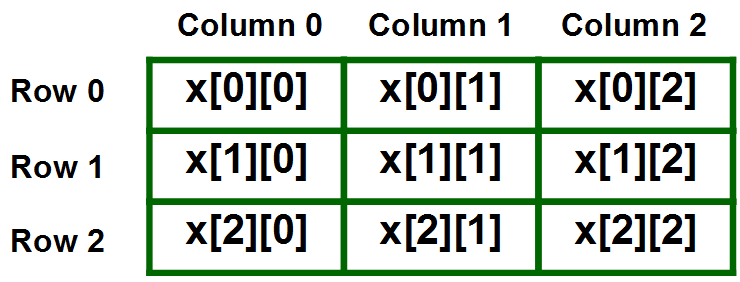
exemplo com duas dimensões:
Exemplo com 3 dimensões:
void OnStart() { //--- // initializing the 2-dimensional array. int x[3][2] = {{0,1}, {2,3}, {4,5}}; for(int i = 0; i < 3; i++) { for(int j = 0; j < 2; j++) { Print("Element at x[",i,"][",j,"]: ", x[i][j]); } } // initializing the 3-dimensional array int z[2][3][2] = { {{0,1},{2,3},{4,5}} ,{{6,7},{8,9},{10,11}} }; for(int i = 0; i < 2; ++i) { for(int j = 0; j < 3; ++j) { for(int k = 0; k < 2; ++k) { Print("Element at x[",i,"][",j,"][",k,"] = ",z[i][j][k]); } } } }
exemplo com duas dimensões:
Exemplo com 3 dimensões:
Minha tentativa baseado em observações sobre C++
int vetor[30] = {1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30}; int tabela[6][5]; int contador = 0; for(int linha = 0; linha < 6; linha++) { for(int coluna = 0; coluna < 5; coluna++) { tabela[linha][coluna] = vetor[contador]; contador++; } }
CONSEGUI! Atenção para:
1) A declaração do contador ficar acima dos loops for (senão ele nunca avança além dos 5 primeiros valores).
E
2) Estabelecer o tamanho do Array bidimensional antes do loop (linhas e colunas). Não dá para preenchê-lo com os dados do Array unidimensional sem antes precisar o número de linhas e colunas (se eu estiver errado por favor me corrijam).
ArrayPrint do vetor:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
ArrayPrint da tabela:
[,0][,1][,2][,3][,4]
[0,] 1 2 3 4 5
[1,] 6 7 8 9 10
[2,] 11 12 13 14 15
[3,] 16 17 18 19 20
[4,] 21 22 23 24 25
[5,] 26 27 28 29 30
Agradecimento especial ao Jonathan Pereira pelos ensinamentos pontuais.

- www.mql5.com
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso

Olá pessoal!
Preciso transformar uma Matriz de uma dimensão apenas em uma Matriz de duas dimensões OU posso preencher a Matriz de duas dimensões com os mesmos dados logo de cara. Um exemplo para ilustrar:
(matriz com de uma dimensão com 10 valores):
[2,4,6,8,10,1,2,3,4,5]
(coloquei essa mesma questão no fórum em inglês, se a moderação exigir que eu mantenha apenas em uma língua, deixo apenas essa aqui)
Obrigado pela atenção, um abraço!