소스에서 시작해야 합니다.
링크가 필요하지 않습니다. 그렇지 않으면 달성하려는 것을 실제로 이해하는 사람이 거의 없는 또 다른 Econometrics-2 분기가 있습니다. 당신의 자신의 말로, faa !
나는 최근에 뚱뚱한 꼬리가 특이치, 종종 단일 값으로 인해 발생한다는 기사를 읽었습니다. 생각이 달랐던 걸로 기억합니다. 내가 틀릴 수도 있지만.
내가 이해하고 있습니까? 할 일이 없어서 포럼 회원들 사이에서 노골적인 무지와 씨름하고 있습니다. 돈 키호테. 여기엔 아무 것도 읽지 않는다고 자부하는 사람들이 많이 있습니다. 그냥 어둠! 그리고 여기에 두 개의 링크가 있습니다.
아니요. 원본에 대해서만 토론할 수 있습니다. "현대 박람회"는 허용되지 않습니다.
정확히 표현되지 않을 수도 있습니다. 링크는 원본과 완전히 일치하며 더 넓을 수 있습니다. 하지만 그게 요점이 아닙니다.
우회합시다.
프로그래밍 언어 연산자 의 의미는 무엇입니까? 이것은 프로그램, 이 명령문이 실행하는 코드입니다.
ARMA 모델이란 무엇입니까? 이 모델을 실행하는 코드입니다.
우리가 이 해석에서 벗어나면, 우리는 분명히 문맹자에 대한 다양한 해석과 무지한 수준의 왜곡에 빠져들 것입니다.
이 포럼에서 프로그램(실행 코드)은 의미론입니다. 따라서 Box 책의 의미는 예를 들어 STATISTICS와 같은 프로그램으로 거래에 유용한 공식과 단어의 가치를 제공합니다.
시작하자.
ARIMA 모델은 ARIMA(p,d,q) 또는 AR(p) I(d) MA(q)로 작성됩니다. 여기서 p와 q는 회귀 방정식의 시차 수이고 d는 횟수입니다. 오리지널 시리즈의 차별화.
먼저 ARMA(ARSS)를 가져와서 lag 값의 개수를 선택합시다. EURUSD 시계는 2011.11.28 00:00부터 2011.12.23 21:00까지입니다. 이것은 각각 118개의 감시 막대가 있고 총 472개의 막대가 있는 정수 주입니다.
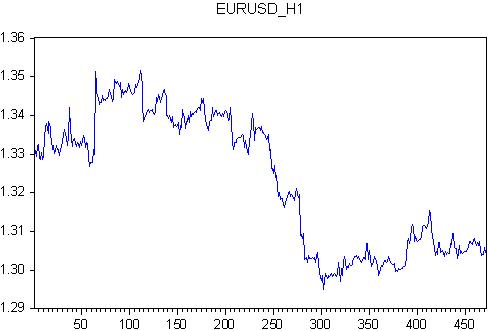
이 인용문에 대해 회귀 방정식을 작성합니다.
유로화 ar(1) ma(1) c @trend
저것들. EURUSD 호가는 자기회귀, 오차, 편향(상수) 및 선형 추세를 통해 결정됩니다.
이 회귀의 계수를 추정해 보겠습니다. 우리는 결과를 얻는다

우리는 두 개의 매개변수에 대해 괜찮은 결과를 얻었고 나머지 두 개에 대해서는 나쁜 결과를 얻었습니다. @trend ma(1)은 계수를 추정할 때 매우 큰 오류 값을 가집니다.
이러한 연습의 실제 결과는 무엇입니까?
(1) 수치적 특성을 가진 지표로 프로그래밍할 수 있는 몇 가지 방정식을 얻었습니다.
(2) 우리의 지표는 호가의 이전 값과 호가와 회귀 값의 차이만을 고려합니다. 후자의 지표는 고려하지 않습니다. 따라서 지표가 더 정확합니다.
(3) TA에 대한 완전히 새로운 결과: 지표의 계수는 랜덤 변수입니다. 최소한 하나의 결론: 현재 견적에 대한 계수 적응이 없는 지표는 의미가 없습니다.
.....
(2) 우리의 지표는 호가의 이전 값과 호가와 회귀 값의 차이만을 고려합니다. 후자의 지표는 고려하지 않습니다. 따라서 지표가 더 정확합니다.
(3) TA에 대한 완전히 새로운 결과: 지표의 계수는 랜덤 변수입니다. 최소한 하나의 결론: 현재 견적에 대한 계수 적응이 없는 지표는 의미가 없습니다.
(2) 더 정확하게는 무엇입니까?
(3) 지표가 더 정확하지만 의미가 없다는 사실에서 얻는 이익은 무엇입니까?
(2) 더 정확하게는 무엇입니까?
(3) 지표가 더 정확하지만 의미가 없다는 사실에서 얻는 이익은 무엇입니까?
자기 이익만 있을 것입니다.
계량경제학 은 자기 이익을 위한 것이 아니라 글로벌 위기를 위한 것입니다.
지표가 정확히 무엇인지는 중요하지 않으며 의미가 없다는 의미는 아닙니다. 식물학자에게 가장 중요한 것은 손에 들어오는 모든 것을 계산하는 것입니다. topicstater는 마침내 EViews를 마스터했으며 일부 데이터를 프로그램에 푸시하고 그 대가로 의미 없는 숫자를 얻을 수 있게 되어 기쁩니다. 여기서 중요한 것은 결과가 아니라 과정에서 나오는 버즈입니다.
계량 경제학자는 우리가 그와 함께 기뻐하기를 바랍니다. 그러므로 상업주의로 그의 기분을 망치지 말고 계량 경제학의 무의미한 가능성을 기뻐합시다.
우리는 또한 잠시 침묵의 시간으로 세계 위기 Jenkins와 Box의 참전 용사들에 대한 추모를 기릴 것입니다. 1분 동안 그들에게 욕하지 않고 버텨야 합니다. 모든 사람에게 즉시 적용되는 것은 아니지만 시도해야 합니다.
38년 전인 1974년, Box와 Jenkins의 전설적인 책 "시계열 분석"이 출판되었습니다. 이 책은 시계열의 분석과 예측에 큰 영향을 미쳤고 지금도 영향을 미치고 있습니다. 지금까지 미국 정부 기관에서는 이 모델을 수정하여 예측을 하고 있지만, 많은 새로운 것들이 등장했습니다. 그러나 우리는 베테랑을 기억합니다.
이 책은 ARSS 또는 ARPSS의 러시아어 번역에서 ARMA, ARIMA 모델을 제시합니다.
이 모델에 대해 많은 오해가 있습니다. 제목부터 시작하겠습니다.
영어: ARSS - 자기회귀 및 이동 평균.
AR - 자기회귀 - 이것은 이해할 수 있습니다. 시계열의 마지막 구성원은 이전 지연 값을 통해 결정됩니다. 거의 모든 지표에 대한 일반적인 아이디어.
SS - 이동 평균. 여기 캐치가 있습니다. 그것은 자동차와 관련이 없습니다. 노이즈 모델링에 관한 것입니다. 저것들. 시장 모델은 처음에 AR로 설명되는 결정론적 요소와 MA가 설명하는 노이즈라는 두 가지 구성 요소로 구성됩니다. 지표의 경우 이것은 분명히 1974년 이후의 새로운 단어입니다!
ARPSS 형식의 AARSS 모델 확장이 있습니다. 여기서 P는 통합 모델입니다. 여기에 도착이라고 하는 것이 있습니다. 통합은 차별화를 의미합니다! 저것들. kotir의 인접한 막대 사이의 차이를 가져 가라!
그리고 Box와 Jenkins의 마지막 업적. VR의 비정상성을 명시적으로 인식하고 비정상 시계열을 정상 시계열로 변환하는 기술을 제안한다. 문자 "P"는 고정되지 않은 VR을 고정된 상태로 변환하는 방법일 뿐입니다.
주제에서 더 나아가 이 모델에 대한 계산 결과를 제공할 것입니다. 나는 Faure에 대한 결과와 적용 가능성에 대해 논의할 것을 제안합니다. 모델은 문서와 소프트웨어 구현 모두에서 통계에서 충분히 충분히 고려됩니다. 이 문제에서는 STATISTICS보다 열등한 것 같지만 EViews를 사용할 것입니다.
시작하겠습니다.