첫째, 특정 시점 t의 가격 상승은 당연히 어느 정도의 가치를 가지며 이를 D0으로 표시합니다. 가정해 봅시다.
다음... 이제 t=0에서는 가격에 아무런 영향이 없으며 외부 충격으로 인한 가격 상승도 없다는 것을 이해합니다. 그러나 우리는 다시 델타 D0이라고 부릅니다.
그런 다음 dt/tau를 공식에 넣었는데, 이는 어쨌든 1/C^2입니다. 즉, 충격에 가속도를 주었으므로 어쨌든 기하학적 회귀를 움직일 것입니다. 왜 그래야 할까요? 결국, 우리는 아직 정의하지 않았습니다-이 충격이 무엇인지 ...
글쎄요, 일반적으로...
1. Do는 가격 증분이 아니라 t=0 시점에 가격에 영향을 미치는 힘의 초기 잠재력입니다.
2. 기사에서: ".... 평형 상태인 시장 가격은 가격과 동일한 차원에서 측정할 크기와 가치를 가진 어떤 외력 D(t)의 작용에 의해서만 변할 수 있다고 가정합니다.
또한 이 힘의 영향이 시작된 시점부터 시간이 경과함에 따라 시장 가격 P(t)의 변화는 아직 알려지지 않은 어떤 규칙성에 의해 0 값에서 지속적으로 증가하여 무한대에서 P(∞) = D0 값에 도달하는 경향이 있다고 가정해 봅시다. 즉, D0은 이 영향력의 성격과 부호에 따라 시장 가격이 유한하게 증가하거나 감소하는 것을 의미합니다.
또한 D(t=0) = D0이라고 가정합니다. 또한 무한대의 시간 dt 동안 영향력은 시간 t의 순간까지 남은 힘 D(t)에 비례하여 dD(t) 값만큼 감소한다고 가정해 보겠습니다:
이로부터 시간 t에 대한 D(t)의 지수 의존성을 다음과 같은 식으로 구할 수 있습니다:
(1)
여기서
t - 불안정한 힘의 영향이 시작된 시점부터 시계열 단위(초, 분, 시간, 일, 주, 수십 년, 월, 년)로 표시된 시간입니다;
τ (타우) - 프로세스의 시간 상수와 수치적으로 동일한 비례 계수, 초(분, 시간, 일, 주, 수십 년, 월, 년)."
1/s^2의 차원은 어디에서 찾았나요? 그 비율에는 차원이 없습니다. 저는 그냥 넣은 것이 아니라, 어떤 과정에 작용하는 힘의 변화 (감소) 속도는 힘 자체에 비례한다는 가설을 세웠고, 이 가설은 논리적으로 모순되지 않는 것으로 완전히 확인되었습니다. 비례 계수로서 시간, 차원의 역수인 a(알파) = 1/타우의 비율을 도입했습니다. a (알파)는 시스템의 임피던스, 즉 프로세스의 흐름에 대한 시스템의 저항을 의미하며, 타우는 나중에 밝혀진 것처럼 라플라스 변환에서 시간의 이미지이며 프로세스의 분석을 미분 영역에서 일반 영역으로 가져갈 수 있습니다. 즉, 모든 프로세스에는 우리와 다른 고유한 시간이 있으며, 타우는 시간의 '번역자' 역할을 합니다. 이 글의 앞부분에서 타우를 추정하는 방법을 설명했습니다:
이제 해당 시간 t에 대한 함수 f의 값을 알고 있다면 이 방정식에서 매개변수 n, τ, 계수 β는 다음과 같이 결정됩니다:
(12)
(13)
(14)
여기서:
시간 t와 시간 t의 해당 순간에 대한 함수 f의 값은 불안정화 시작부터 시간 h0, h1,..., һk의 순간까지 시장 가격 P0, P1,..., Pk의 실제 값에 의해 결정되며, 그 간격의 중간을 수치 미분으로 참조합니다:
비공개 메시지로 연락하여 조건에 대해 알아보세요.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
지표는 유료인가요? 코드베이스에 게시되어 있으니 마음껏 사용하세요!
새 문서 시장 가격 예측을 위한 범용 회귀 모델이 게시되었습니다:
작성자: Юсуфходжа
좋은 기사입니다.
매우 인상적입니다.
유감이지만 기사의 맨 처음에 실수가 있습니다.
첫째, 특정 시점 t의 가격 상승은 당연히 어느 정도의 가치를 가지며 이를 D0으로 표시합니다. 가정해 봅시다.
다음... 이제 t=0에서는 가격에 아무런 영향이 없으며 외부 충격으로 인한 가격 상승도 없다는 것을 이해합니다. 그러나 우리는 다시 델타 D0이라고 부릅니다.
그런 다음 dt/tau를 공식에 넣었는데, 이는 어쨌든 1/C^2입니다. 즉, 충격에 가속도를 주었으므로 어쨌든 기하학적 회귀를 움직일 것입니다. 왜 그래야 할까요? 결국, 우리는 아직 정의하지 않았습니다-이 충격이 무엇인지 ...
글쎄요, 일반적으로.
유감이지만 기사의 맨 처음에 실수가 있습니다.
첫째, 특정 시점 t의 가격 상승은 당연히 어느 정도의 가치를 가지며 이를 D0으로 표시합니다. 가정해 봅시다.
다음... 이제 t=0에서는 가격에 아무런 영향이 없으며 외부 충격으로 인한 가격 상승도 없다는 것을 이해합니다. 그러나 우리는 다시 델타 D0이라고 부릅니다.
그런 다음 dt/tau를 공식에 넣었는데, 이는 어쨌든 1/C^2입니다. 즉, 충격에 가속도를 주었으므로 어쨌든 기하학적 회귀를 움직일 것입니다. 왜 그래야 할까요? 결국, 우리는 아직 정의하지 않았습니다-이 충격이 무엇인지 ...
글쎄요, 일반적으로...
1. Do는 가격 증분이 아니라 t=0 시점에 가격에 영향을 미치는 힘의 초기 잠재력입니다.
2. 기사에서: ".... 평형 상태인 시장 가격은 가격과 동일한 차원에서 측정할 크기와 가치를 가진 어떤 외력 D(t)의 작용에 의해서만 변할 수 있다고 가정합니다.
또한 이 힘의 영향이 시작된 시점부터 시간이 경과함에 따라 시장 가격 P(t)의 변화는 아직 알려지지 않은 어떤 규칙성에 의해 0 값에서 지속적으로 증가하여 무한대에서 P(∞) = D0 값에 도달하는 경향이 있다고 가정해 봅시다. 즉, D0은 이 영향력의 성격과 부호에 따라 시장 가격이 유한하게 증가하거나 감소하는 것을 의미합니다.
또한 D(t=0) = D0이라고 가정합니다. 또한 무한대의 시간 dt 동안 영향력은 시간 t의 순간까지 남은 힘 D(t)에 비례하여 dD(t) 값만큼 감소한다고 가정해 보겠습니다:
이로부터 시간 t에 대한 D(t)의 지수 의존성을 다음과 같은 식으로 구할 수 있습니다:
여기서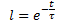
t - 불안정한 힘의 영향이 시작된 시점부터 시계열 단위(초, 분, 시간, 일, 주, 수십 년, 월, 년)로 표시된 시간입니다;
τ (타우) - 프로세스의 시간 상수와 수치적으로 동일한 비례 계수, 초(분, 시간, 일, 주, 수십 년, 월, 년)."
1/s^2의 차원은 어디에서 찾았나요? 그 비율에는 차원이 없습니다. 저는 그냥 넣은 것이 아니라, 어떤 과정에 작용하는 힘의 변화 (감소) 속도는 힘 자체에 비례한다는 가설을 세웠고, 이 가설은 논리적으로 모순되지 않는 것으로 완전히 확인되었습니다. 비례 계수로서 시간, 차원의 역수인 a(알파) = 1/타우의 비율을 도입했습니다. a (알파)는 시스템의 임피던스, 즉 프로세스의 흐름에 대한 시스템의 저항을 의미하며, 타우는 나중에 밝혀진 것처럼 라플라스 변환에서 시간의 이미지이며 프로세스의 분석을 미분 영역에서 일반 영역으로 가져갈 수 있습니다. 즉, 모든 프로세스에는 우리와 다른 고유한 시간이 있으며, 타우는 시간의 '번역자' 역할을 합니다. 이 글의 앞부분에서 타우를 추정하는 방법을 설명했습니다:
이제 해당 시간 t에 대한 함수 f의 값을 알고 있다면 이 방정식에서 매개변수 n, τ, 계수 β는 다음과 같이 결정됩니다:
여기서:
시간 t와 시간 t의 해당 순간에 대한 함수 f의 값은 불안정화 시작부터 시간 h0, h1,..., һk의 순간까지 시장 가격 P0, P1,..., Pk의 실제 값에 의해 결정되며, 그 간격의 중간을 수치 미분으로 참조합니다:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); 등등;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; 등등.