В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
ここに矛盾はない。需給の基本法則はこうした効果を予測している。ここで重要なのは、モデル全体を動的に考えるべきだということである。私が言っていることを理解するためには、まず古典的な静的需給モデルを考える必要がある(「今、ここ」の場合):
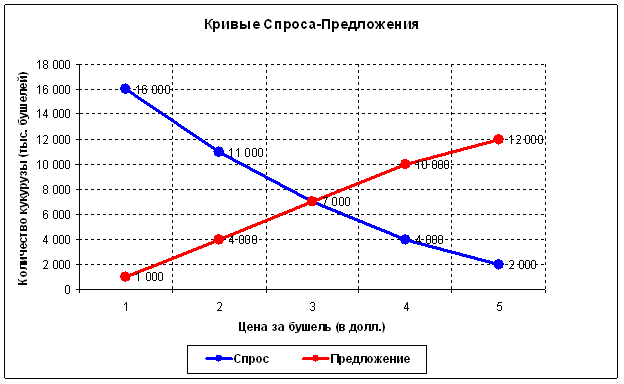
つまり、ある財(この場合、7000ブッシェル、価格3ドル)の交換が最大効率的に行われる地点は、各時点で1つだけである。他のすべての時点では、より少ない財がより少ない貨幣と交換される。マクロ経済の状況は常に変化しているため、この効率的交換点自体も変化していることになる。しかし、市場は効率的であり、その主な仕事は、そのようなポイント、つまりまさに均衡価格(「買いたい人はすべて買い、売りたい人はすべて売る」)を常に探し求めることである。この時点で最大量の商品が交換されるため、この時点での取引量は 大きくなるはずである。市場がこのような量を実現するには時間が かかる。この理論は、出来高の蓄積の効果を予測している:
市場は、ほとんどの時間、統合段階(最大効率領域)にある。
しかし、世界経済 全体は常に進化している。新技術が登場し、生活水準が向上する。その結果、一方ではより多くの財やサービスが必要とされ、他方では科学技術の進歩により、より多くの財やサービスを生産することが可能になる。流動性は時間とともに増大する。世界市場の取引量は増大し、その結果、ボラティリティは増大し、危機の規模は縮小する。時間の経過とともに需要が増加すると、価格は上昇する。同時に、科学技術の進歩は、この需要により多くの財やサービスを提供する。その結果、均衡点は時間の経過とともに一般的に上方へ、右方へと移動する。この点を常にさまよう市場もまた、一般的に成長する(価格が高くなる傾向がある)。

これが、まさにこの「トレンド性効果」に由来する。すべて数学的計算でうまく辻褄が合うので、ただただ息をのむばかりである。いずれにせよ、経済効果は数学的な依存関係を説明するはずだが、その逆はありえない。
酔っぱらった船乗りを例えに出すと、ステップの大きさが違ってくる。大雑把に言えば、パブから移動する場合、1歩の長さは80センチ、(パブへ)戻る場合は60センチである。トレンドは同じで、市場の下降は上昇よりも速いことも知られている。そして、この記事ではすべてのステップが同じ+1または-1である。
だから、このモデルは適切とは言えない。これは単なるコインであり、その分布特性は長い間知られ、研究されてきた。
酔っぱらいの船乗りをたとえるなら、ステップの大きさは異なる。大雑把に言えば、パブから移動する場合、1歩の長さは80センチで、(パブへ)戻る場合は60センチである。トレンドは同じで、市場の下降は上昇よりも速いことも知られている。そして、記事ではすべてのステップは同じ+1または-1 "です。
このコインには、幾何学的ブラウン運動モデルという連続的な類型がある。これについては、http://algoritmus.ru/?p=2889。
「アルゴリズム取引の問題解決への確率的アプローチ」。
著者: アルセン・ヤコブレフ、グリゴリー・フラングリディ
発行:「D-Shtrich」誌16号/6 2010年9月
この記事は私の記事と同じアイデアを持っているが、ただ数学が多いだけである。離散モデルを取るか連続モデルを取るかは好みの問題だ。どちらも同じだ。一方のモデルには積分があり、もう一方には和があるだけだ。コインモデルはすでに小学生に理解されているが、連続モデルは学生にしか理解されていない。
「市場の下降が上昇より速いことも知られている」-これは私にとって非常に興味深い。
「だから、このモデルは適切とは言えない。その分布特性は長い間知られ、研究されてきたコインに過ぎない。"- どんなモデルも現実を100%適切に描写することはできない。市場モデルとしてのコインレートも含めて。だからこそ、市場により適切に対応するために、トレンドのあるコインのモデルを考案しなければならなかったのだ。
- 2010.09.13
- val
- algoritmus.ru
なぜコインなのか?コインには2つの面がある。理想的なランダム・ウォークが直線(アナログ:上、下)上をさまようだけである。すなわち、2次元のランダム・ウォークである。上記のチャートから、このような市場の状態は実際にはモデル化されていないことがわかります。
図2の黄色の曲線が最もフラットに近い。パラメータをa=-0.5とすると、最もタイトな平坦線が得られる。つまり、コインの表と裏の2つの面があれば、フラットを表現するには十分なのである。ちなみに、この記事でいう「フラット」とは「アンチ・トレンド」のことである。
しかし、そうするとチャート全体が水平になり、私が正しく理解しているのであれば、実際の市場では、急激なトレンドと硬い横ばいの両方が存在し得る。独立性とは、コインの第3の面が必要なことです。単純に、市場が平面上をさまよっているのは、時間的要因がさまよっているからであり、コインはさまよいの一次元モデルを持っており、このモデルの時間に対する単純な(さまよいのない)掃引は全く正しくない。しかし、この記事は非常に有益である。
トレンドのあるコインのモデルでは、トレンド性は相場の全期間を通じて一定とみなされます。そして、実質レートのトレンディネス指標が示すように、トレンディネスは常に変化している。そして、長い期間(数年間)の平均においてのみ、トレンディネスが一定として測定されるのです。
トレンド付きコインレート」のモデルを市場に対応させるには、複雑化させればよい。パラメータ "a "をカオス的に時間依存にすることもできるし、何か別のものを発明することもできる。クリエイティブなことだ。厳密に言えば、2つ目の次元を導入する必要はないが、必要であれば、"a "の隣に2つ目のカオス乗数を追加することができる。
例えば、このNew Moving Mini-Max テクニカル分析インディケータとMQL5への実装を テストするには、一定のトレンドを持つ単純なモデルが必要です。 このようなインディケータを実際のコースで扱うのは現実的ではありませんが、一定のトレンドを持つ単純なモデルでテストするのは良いことでしょう。
...離散モデルを取るか連続モデルを取るかは好みの問題だ。どちらも同じだ。片方のモデルには積分があり、もう片方には和があるだけだ。そして、コインモデルはすでに小学生に理解されており、連続モデルは学生にしか理解されていない...。
そこに間違いがある。
1.連続モデルから離散モデルへの移行は正しく行われなければならない。
2.連続モデルも離散モデルも同じであるが、+と-の段差が同じでなければならない。その大きさ。
3.分析するために小節を取った。片方のモデルだけが積分を持ち、もう片方は和を持つ。" すべての棒グラフが同じであることを証明しなさい。証明できますか?
4.この性質を持つチャートは1つだけです。renkoチャートです。+1 -1(https://www.mql5.com/ja/code/9447#25419) と置き換えることができます。
記事へのリンクをありがとう。読みました。ARFIMAモデル、ランダムウォークを使うことを提案しています。これらは異なるモデルです。以下の記事を、あなたと著者の両方で読むと面白いでしょう。そこでは、あなたの提案する市場モデルが適切であることが証明されている。言葉で主張するだけでなく、数学的に証明されている...そして、この数字の計算を考えると...
H.Y.ただ、多くの人がこの妥当性という美しい言葉を理解しているが、その計算方法さえ知らない。あなたは投稿の中で、100%適切なモデルは存在しないと書いている。まったく同感だ。問題は、提案されたモデルが市場に対して20%、30%、あるいは99.999999999%のどれだけの妥当性があるかということだ。
スタックをモデル化してみよう。スタックには明確な構造があり、スタックは上下に一定数 の点の順序を見る。
ジェネレータはすべてのセルを通過し(+1 -1 ではなく、ランダムなボリュームの生成でもよい)、スタックのすべてのセルがジェネレータによって通過された後、スタックの中間点をどこに移動するかの計算が行われる。
32768個のランダムを生成した後、SRANDを再起動するのを忘れないように。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事 ランダムウォーク理論とトレンドインディケータ はパブリッシュされました:
ランダムウォークは現実のマーケットデータと実によく似ていますが、大きな特徴がいくつかあります。本稿ではコインン投げゲームを使用するシミュレーションでランダムウォークのプロパティを考察します。データのプロパティを調査するためトレンドインディケータを作成します。
作者: Гребенев Вячеслав