筆者(なぜかニックネームなし)へ。
同じ問題は他の方法でも解決できる。冗長変数や欠落変数のテストがあります。それをやって、あなたの結果と比較することもできます。しかし、.csv形式のファイルがすべて必要です。
ソースはmasterdata.zipアーカイブにあると思います。
我々は変数を選択した後、それらからいくつかの関係を作らなければならない。その中で、価格は従属変数(関数)となり、他の指標は独立変数となる。以下に概略式を示す:
価格 price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 は直前の値を意味する。この指標は価格から分析的に導き出されたものなので、これは自然なことです。価格がインクリメントであることを考慮し、指標のインクリメントを取ることにしましょう。怠惰のため、すべての指標を取りません。この式を最小二乗法で推定してみよう:
方程式の係数の推定値が得られた。最後の列は非常に興味深い。これは、対応する係数がゼロに等しい確率を意味する。つまり、対応する係数がゼロに等しいという仮説を棄却することはできないと考えることができる。したがって、R2乗はとんでもない値になっている。
私は、指標の分類を扱うのは無駄だと結論づけます。なぜなら、指標の分類は価格の上昇とは何の関係もないからです。
それとも私は間違っているのだろうか?
...それとも私が間違っているのだろうか?
その通りだと思います :-)
faa1947 さん、質問があります。 いくつか明確にしたいことがあるんだ。これは、私があなたの方程式からデータを計算した方法です:
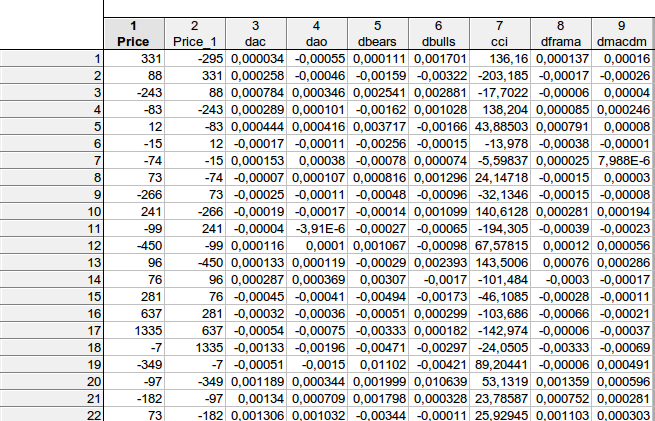
表のデータは、あなたの計算式と一致していますか?price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
そして、次のような結果が得られました:
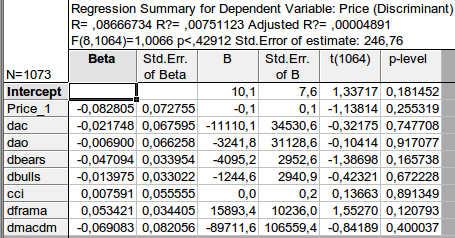
一旦変数を選択したら、それらの変数から、価格を従属変数(関数)とし、他の指標を独立変数とする関係を作らなければならない。以下に概略式を示す:
価格 price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 は直前の値を意味する。この指標は価格から分析的に導き出されたものなので、これは自然なことです。価格がインクリメントであることを考慮し、指標のインクリメントを取ることにしましょう。怠惰のため、すべての指標を取りません。この式を最小二乗法で推定してみましょう:
方程式の係数の推定値が得られた。最後の列は非常に興味深い。これは、対応する係数がゼロに等しい確率を意味する。つまり、対応する係数がゼロに等しいという仮説を棄却することはできないと考えることができる。したがって、R2乗はとんでもない値になっている。
私は、指標の分類を扱うのは無駄だと結論づけます。なぜなら、指標の分類は価格の上昇とは何の関係もないからです。
それとも私が間違っているのでしょうか?
使用した統計手法の名前を教えてください。入力が指標で、出力が将来の価格である線形回帰式の構築ですか?それは正しいですか?FXは線形決定論的システムではないので、これは使えません。判別分析には異なるタスクがあり、システムの外部記述に基づいてパターン認識のモデルを構築します。
もし、価格変動を分析するために指標を分類することが無駄であれば、テクニカル分析は無意味になってしまいます。幸いなことに、価格は無秩序に動くことはなく、過去の出来事を記憶している。
あなたは正しいようだ :-)
faa1947 さん、質問があります。 いくつか明確にしたいことがあるんだ。これは、私があなたの式からデータを計算した方法です:
表のデータは、あなたの計算式と一致していますか?price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
そして、次のような結果が得られた:
生データは以下のようになる:
方程式は次のようになる:
推定方程式:
=========================
PRICE = C(1)*PRICE(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Substituted Coefficients:
=========================
price = -0.0228102658125*price(-1) + 12005.8974278*dac(-1) + 4033.10946937*dao(-1) + 3176.11232129*dbears(-1) - 6021.36196728*dbulls(-1) - 0.102710105369*cci(-1) - 11487.4273249*dframa(-1) + 62535.3387412*dmacdm(-1)
あなたの計算が理解できない。私はラグ値(前回値)を使用する原則を持っています。これによって予測が可能になる。ラグ -1 が1番目のオブザベーションに対応するならば、従属変数は、新しい、予測された、観察されていないオブザベーションに対応します。
p-levelとは何ですか?私にとっては、対応する係数がゼロである確率です。
使用した統計手法の名前を教えてください。入力が指標で出力が将来の価格である線形回帰式でしたか?正しいですか?
回帰は最小二乗法を用いて推定されました。これは予測に使用できます。
FXは線形決定論的システムではないので、これは使えません。
線形であるとすれば、それは特定の例においてです。係数さえも確率変数として扱われるため、決定論的ではありません。すべての係数は計算されたものではなく、推定されたものである。番目の列は、係数推定の標準誤差を示している。 巨大であることに注意されたい。
価格の上昇を分析するための指標の分類が無意味であったとしたら、テクニカル分析は無意味になってしまう。
その通りであり、そう考えているのは私だけではないと断言する。TAは科学ではなく、占星術の一種である。もともとは300年前、コティルを視覚化するためのシステムだった。それ以来、非常に進化してきた。それ以外はすべて、奇跡の分野におけるピノキオのためのものだ。あなたの記事には、規則的で再現性のある考え方があり、私は満足している。
価格の上昇を分析するための指標の分類が役に立たない場合
ここでは、指標の特殊なケースを分析した。特定のインディケータやその使用が相場と関係があることを証明する必要があります。TAがこの問題を考慮することはありません。
幸いなことに、価格は無秩序に動くのではなく、過去の出来事を記憶しています。
すべての計量経済学は、相場には決定論的要素(自己相関、記憶)とノイズがあるという仮定の上に成り立っています。
判別分析には異なる課題があり、システムの外部記述に基づいてパターン認識のためのモデルを構築する。
タスクは明確である。しかし、得られた結果が信頼できるかどうかが問題である。問題は分類ではなく(それも問題の一部であり、解決される必要がある)、結果として得られる予測に対する信頼である。それこそが問題なのだ。
あなたの計算が理解できない。私の原則はラグ値(前回の値)を使うことだ。これは予測を可能にします。ラグ -1 が1番目のオブザベーションに対応するならば、従属変数は、新しい、予測された、観察されていないオブザベーションに対応します。
p-levelとは何ですか?私にとっては、対応する係数がゼロである確率です。
faa1947, ラグのある表(最初の数行 - 表全体をあてはめることはできません)を示しました。しかし、最初に指標差を計算したので、行の総数は1074行ではなく1073行になりました。 そして、従属変数Priceを 一歩進めました。
その結果、1行目の例では
331 =C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, ただし、以下のようになる。
price = c(1)*price(-1) + c(2)*dac(-1) + c(3)*dao(-1) + c(4)*dbears(-1) + c(5)*dbulls(-1) + c(6)*cci(-1) + c(7)*dframa(-1) + c(8)*dmacdm(-1)
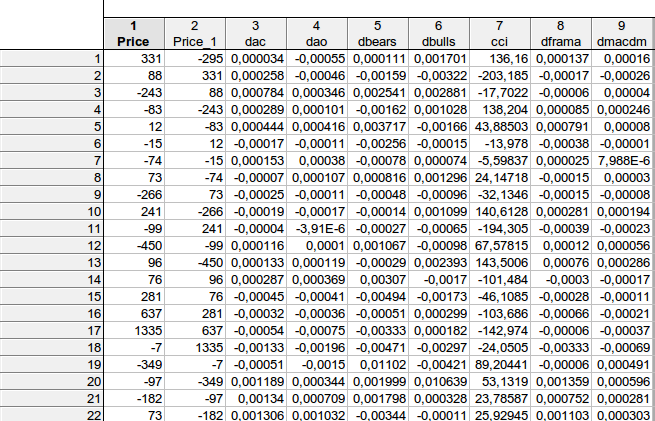
一般的に、私はおおよそ同じような結果を得ました - 考えられる係数がゼロに等しいという帰無仮説を棄却する 方法はありません...
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
新しい記事 トレーディングシステム作成のための判別分析の利用 はパブリッシュされました:
作者: ArtemGaleev