回帰分析の基礎」というテーマで、以下の文献をご紹介しています。
Davidson,Russell and James G.マッキノン(1993)。Estimation and Inference inEconometrics, Oxford: オックスフォード大学出版 局.
グリーン,ウィリアム・H.(2008). 計量経済学的分析、第6版、Upper Saddle River, NJ: Prentice-Hall.
Johnston, Jack and John Enrico DiNardo (1997). 計量経済学的手法、第4版、ニューヨーク:マグロウヒル 社。
Pindyck, Robert S. and Daniel L. Rubinfeld (1998). Econometric Models and Economic Forecast, 4th edition, New York: McGraw-Hill.
ウールドリッジ、ジェフリーM.(2000). Introductory Econometrics: A Modern Approach(入門計量経済学:現代的アプローチ). Cincinnati, OH: South-Western College Publishing.
回帰の例を挙げましょう。回帰とは、関数(従属変数)が引数(独立変数、回帰子)に依存することにほかなりません。回帰計算をする際には、いくつかのステップがあります。
1.方程式を書き出す必要がある。
私は、注目されているMAを使いますが、加重しているので、私にとっては寛容で、前の5本のバー(ラグ値)を使って計算します。という形で式を書いています。
eurusd = c(1)*eurusd(-1)+c(2)*eurusd(-2)+c(3)*eurusd(-3)+c(4)*eurusd(-4)+c(5)*eurusd(-5)とします。
2.見積もり
この式の係数c(i)を推定して、MAの曲線が初期のEURUSD_H1年の系列にできるだけ対応するようにする必要があります。未知の係数を評価した結果を得ることができる。
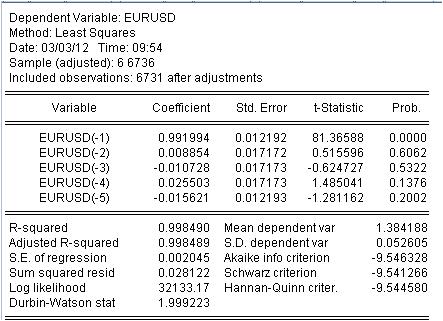
重み付けされたMAの値を取得しました。方程式があるんです。
eurusd = 0.991993934254*eurusd(-1) + 0.00885362355538*eurusd(-2) - 0.0107282369642*eurusd(-3) + 0.0255027160774*eurusd(-4) - 0.0156205779585*eurusd(-5)
。
3.結果
どのような結果が出るのでしょうか。
3.1 まず、マッハの方程式そのものについて。ちょっとしたニュアンスにも気を配りたい。平均を計算する単純なマスクを計算するとき、なぜか区間の途中では記録せず、その終点で記録する。回帰は、以前の値をもとに最新の値を算出するために使用される。
3.2 比率は定数ではなく、独自の偏差を持つ確率変数であることが判明した。
3.3.最後の欄は、与えられた係数がゼロでない確率が全くないことを表している。
4.方程式を使った作業
それでは、ウェイトミックスを見てみましょう。

マシュカはコチエをしっかり覆ってしまって見えないが、コチエとマシュカにはまだ齟齬がある。これらの矛盾の統計は以下の通りです。

137ポイントから215ポイントまで大きく散らばっているのがわかる。標準偏差=20点なのに。
結論
回帰を利用した統計的特性がわかっているマスクの中では、異例の高画質を実現していただきました。
最後の1枚です。ユスフ!電車に乗るな、もう1スレで視聴者を笑わせるな。
回帰のテーマの文献や応用を議論する準備ができている。
3.結果
どのような結果が出るのでしょうか。
3.1 まず、マッハの式そのものについて。ここでひとつ、微妙な点を指摘しておきたい。平均をとって単純なマスクを計算するとき、なぜかこの平均を区間の真ん中に置かず、端に置いてしまうのです。回帰は、以前の値をもとに最新の値を算出するために使用される。
3.2 比率は定数ではなく、確率変数であることが判明!
3.3 最後の欄は、与えられた係数が0である確率が0でないことを述べている。
1.傷口に塩を塗るようで申し訳ないのですが、とにかく元のシリーズは非定常なのです。
2) この確率はほとんどゼロではありません。
3.多重共線性のチェックをしましたか?IMHO マルチコリニアリティを排除すれば、残る変数は1つだけです。重要なファクターは決まっているのか?
4.5つの変数について、観測値はいくつですか?
どうしてそんなに文才があるんですか?
1.傷口に塩を塗るようで申し訳ないのですが、とにかく元のシリーズは非定常なのです。
もちろん、他の人には興味はありません。
2.その確率はほとんどゼロでは ありません。
そんなことはありません。0でない場合は、関数型エラーとなります。
3.多重共線性のチェックをしましたか?IMHO マルチコリニアリティを排除すれば、残る変数は1つだけです。重要なファクターは特定できたか?
何が「有意な要因」なのか、私にはわかりませんが、相関係数を見てください。
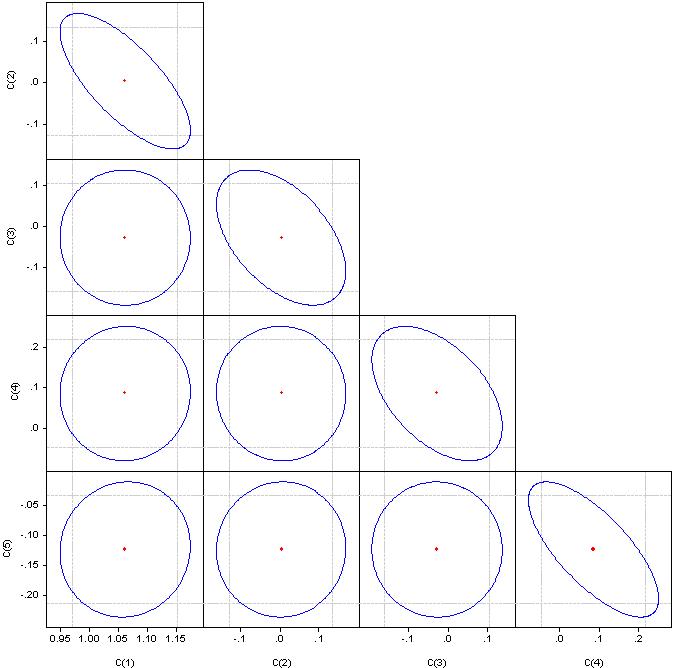
円であれば、相関はゼロです。直線に併合した場合、対応する係数の組の相関は100%となる。
4.5つの変数について、観測値はいくつですか?
6736観測
回帰モデルの 最初のステップは要因の選択である。ステップワイズ回帰を適用しない場合(包含や例外を含む)、手動で選択する必要があります。
多重共線性 - モデルに含まれる 因子変数間の緊密な 依存関係。係数の相関ではなく、要因の相関。
多重共線性の存在は、以下をもたらす。
- モデルのパラメータ の値の歪み、 過大評価する傾向が ある。
- 正規方程式系の弱い条件付け。
- 複雑化 最も重要な 因子の 特徴を決定する プロセス。
多重共線性の一つの指標は、対の相関係数が0.8を超えることであり、ここでは明らかに各因子が強い相関を有している。それを解消するためには、冗長な要素を取り除く必要があります。手動またはステップワイズ回帰のいずれか。
ステップ回帰またはリッジ回帰のパッケージをご覧ください。
それに6736/4は観測回数が多すぎる。ググる必要がありますね。因子の数から最適な観測回数を決定する方法は覚えていません。
私のエコノメトリックススレッドに参加するよう親切にしてください。
ここでは、実際の例をご紹介します。
周期が5のスケールのアナログを構成してみましょう。ただし、バーの係数は3次の多項式にする必要があります。
EViewsでは、EURUSDについて以下のように記述されています。
eurusd pdl(eurusd(-1), 5,3)
もっと身近な形で。
eurusd = + c(5)*eurusd(-1) + c(6)*eurusd(-2) + c(7)*eurusd(-3) + c(8)*eurusd(-4) + c(9)*eurusd(-5) + c(10)*eurusd(-6)
�
OLSで係数を推定し、係数の推定結果を得る。
eurusd = + 0.934972661616*eurusd(-1) + 0.139869148138*eurusd(-2) - 0.093599954464*eurusd(-3) - 0.0264992987207*eurusd(-4) + 0.0801064628352*eurusd(-5) - 0.0348473223286*eurusd(-6))とします。
式の推定に関する統計は以下の通りである。
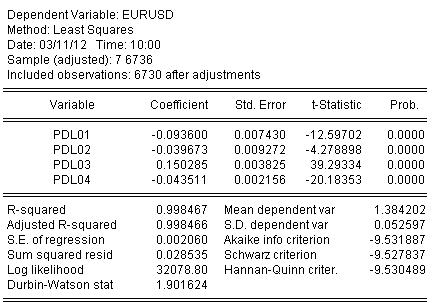
統計から、我々はAlmonのR二乗=0.998467から我々の波による初期商のマッピングの非常に良いレベルを見ることができます。
グラフィック的にはそう見えます。

回帰(アルモンの振れ幅)が元の商を完全に覆ってしまっている。
そして、最後にスプーン1杯のハチミツを。
残量、つまり私たちアルモンのマッシュとオリジナルのコチエの差を見てみましょう。この残差の定常性/非定常性は非常に重要である。

単位根検定では、残差は定常であるとしている。
私たちが使っているマッシュアップは、このように元の商にフィットするレベルではなく、フィット誤差の定常性という特性を持っています。
隣のスレッドからリンクを移動させたいのですが。
これらのリンクは、最も問題のある分野である予後に関するものです。
1つ目は、添付ファイル。参考文献のリストがあります。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
計量経済学」という言葉をグーグル検索すると、膨大な文献がヒットするが、専門家でも理解するのは困難である。ある本にはあることが書いてあり、別の本には別のことが書いてあり、3冊目には、最初の2冊をまとめただけのもので、不正確なところもある。しかし、「本から」のアプローチでは、これらの本を実際に適用することは明確ではありません。インテリがオタクの戯言に堕ちることに興味はない。
このフォーラムにおける他の書籍リスト、例えば統計学に関するものと同様に、参加者の意見として、経済データの測定、つまり計量経済学に関連する教科書、モノグラフ、学位論文、論文、インターネットリソース、ソフトウェアパッケージのリストを集合的に作成することを提案します。しかし、忘れてはならないのは、数理統計学は計量経済学のお姉さんであるということだ。このリストには、テクニカル分析に関連するものは入れない 方がいいと思います。
植物学へのスライドを排除するために、書籍リストの具体的なアプローチを提案します。書籍のアルゴリズムを実装したソフトウェアを知っている場合のみ、リンク(書籍そのもの)を掲載します。EViewsに絞り込んでいます。このプログラムは他と比較して優位性があるわけではなく、メリットとデメリットがありますが、私は計量経済学のルーブリックとして受け止めています。できるだけ広い範囲の問題を一度に概説するために、取扱説明書第2巻の目次を添付します。提案されたアプローチにより、EVIEWSには含まれないが計量経済学で使用されるいくつかの分野、例えばNS、ウェーブレットなどは除外されています。もちろん、そのような番組や書籍の紹介も大歓迎です。
アルゴリズムのソースへのリンクを提供するだけでなく、具体的な計算ができるようになれば、このスレッドの存在価値はなくなるのではないでしょうか。
本のグループ分けには、添付ファイルの章番号を使うことをお勧めします。
だから、応援してください。