では、(目測で)周期が(Xに依存して)常に増加する正弦である、つまり、次のような式だとしたらどうだろう。
一般的な(どこから来るか)。
Y=sin( K*X+T)
ここで、パラメータKもXに依存するとする。ずっと増えたり減ったりしている。リニアなのか、という疑問が生まれます。そもそもリニアに想定しています。すると、A*X+B(線分式)となる。元の式に代入すると、次のようになります。
Y=sin((A*X+B)*X+T)=sin(A*X^2+BX+T)となります。
ここに出発点があります。サイン記号の下の多項式。回帰を実行する...。など- わかりやすく説明できたでしょうか。Matlabでプログラムを作ってあげたいのですが、時間がないので自分でやってください。
これは何のためにあるのか、少し説明させてください。述語を使ったTSのアイデアがあるんです。私が知っているものでは、フーリエと回帰があります。フーリエに応用。基礎となる仮定は、パラメータが定常であることである。通常の正弦波では、すべて問題なく表示されます
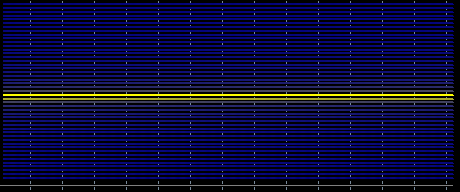
しかし、滑らかに変化する周期をとると、スペクトルは不鮮明になってしまう
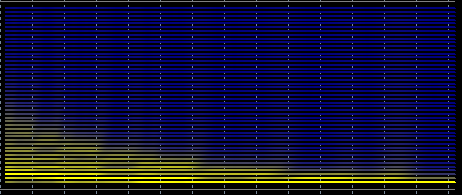
ので、適切な予測はできません。
回帰についても、良いものは得られなかった。
ですから、より「適応的」な他の方法を探す必要があるのです。それが知りたかったのです。
滑らかなカーブを描いていますね。そのため、微分解析の手法が適用できる。周期が変化する正弦であることを知らなくても、最初の数項を保持したテイラー級数展開が使える。そして、その式にいくつか前の項を代入することで、将来の参照値を予測するのに使うことができます。その予測精度の高さに驚かれること請け合いです。誤差はゼロになります。
なぜなら、RFでの分解ではPDFが得られ、1カウント前方を予測する必要はなく、PDFのスケールに収まるカウント数で予測することになり、そこで予測誤差が劇的に増えるからです。
自然はごまかせない。
なぜなら、RFに分解するとFZが得られ、1カウント先ではなく、FZのスケールに収まるカウント数を予測しなければならず、この距離で予測誤差が劇的に大きくなるからです。
自然はごまかせない。
それは理解できる。しかし、パラメータは一定期間変化しないと考えることができる。一番上の写真では、非定常性だけでなく、不適切な手法によっても結果が悪くなることを示したかったのです。
それは明らかです。しかし、しばらくはパラメータが変化しないと考えることも可能である。一番上の写真では、非定常性だけでなく、不適切な手法によっても結果が悪くなることを示したかったのです。
定常的な市場という仮説は、これまで確認されたことはない。したがって、どんなに小さな時間軸であっても、パラメータが一定であると仮定することはできない。
これは何のためにあるのか、少し説明させてください。述語をベースにしたTCのアイデアがあります。私の知る限りでは、フーリエとリグレッションが利用可能です。フーリエに応用。基礎となる仮定は、パラメータが定常であることである。通常の正弦波では、すべて問題なく表示されます
しかし、滑らかに変化する周期をとると、スペクトルは不鮮明になってしまう
ので、適切な予測はできません。
回帰についても、良いものは得られなかった。
ですから、より「適応的」な他の方法を探す必要があるのです。それが知りたかったのです。
ウェーブレットは何ができるのか?
ZS:BaseGroup.ruのコードで MT5用の.dllを作りましたが、まだ実用的な使い方は見つかっていません。http://imglink.ru/pictures/18-01-12/4e3891b89673e8f79e194b5a86a25d41.jpg
定常的な市場という仮説は、これまで確認されたことはない。したがって、どんなに小さな時間軸であっても、パラメータが一定であると仮定することはできない。
完全な定常性ということではなく、おそらくパラメータが多かれ少なかれ安定している部分があると思います。そうでなければ、その戦略がしばらくは有効であることを、他にどう説明すればいいのでしょう。いくつかの戦略を立てて、それを切り替えていくアプローチもありますが、問題は切り替えのタイミングをどう判断するかです。
www.https://www.mql5.com/ru/forum/127297 ここでは、時間的な予測可能性を示す間接的な証拠がある。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
こんな絵があるんです。
このようなシリーズを外挿できる方法論はあるのでしょうか?
誰かこれをニューラルネットワークに組み込んで実験してくれないかな?