フーリエの目利き...
皆さん、こんにちは...。
フーリエ変換について質問があるのですが・・・。
フーリエ変換後、逆変換でハイパスフィルタリング。
変換の範囲外で結果の関数を計算し続けたいのですが...(例を挙げていただければ)
フーリエ変換は周期的な関数にのみ有効なので、これ以上の計算は必要ない。
得られた範囲に周期的な信号があるとする。
その結果、配列の先頭は周期的な配列の続きとなる...。そうだろ？
得られた範囲に周期的な信号があるとする。
その結果、配列の先頭は周期的な配列の続きとなる...。>> でしょ？
どのような配列ですか？
0から2 * PIまでの近似周期でフーリエ変換が行われる。
2*PIは、前周期で既に近似が行われている次の周期では0度。
では、図を見てみると...。
下段に表示されている曲線（赤色）は、以下のパラメータで変換処理した際に得られる緑色の線です。
変換窓の大きさ2^6=64点、使用する周波数数45点。
すなわち、私たちがオリジナルに課した結果としてのカーブの似顔絵を得ることができます ...
図からわかるように、先頭を末尾に置き換えても、本当の結果にはならないのです -。
そこで問題は、緑の線で示すようなカーブをどう続けるか...。
....
そこで問題は、緑色の線で示した曲線の動きをどのように継続させるか...。
フーリエ変換やそれに類する変換のコツですね!
まず市場の非定常性を準定常的な形にするわけですが、少なくとも......。
そうすれば、すべてを静止した正弦波に変えて、好きなところに続けることができるのです。でも...おそらく埒が明かないでしょう...。
それならば、質問の仕方を変えたほうがいいのでは...。
図のような関数は、どのような方法で近似すれば、曲線が小断面で続けられるでしょうか？
それならば、質問の仕方を変えたほうがいいのでは...。
図に示す関数を、小さな面積で曲線が続くように近似するには、どのような方法があるか。
小さな領域では、それを使って外挿することで、どんな近似法でも使うことができる。
ラグランジアンを使っています。
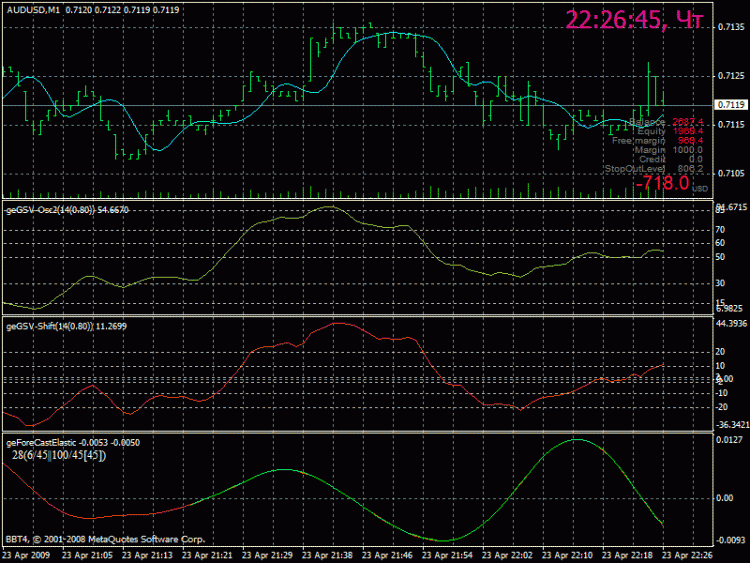
では、図を見てみると...。
下段に表示されている曲線（赤色）は、以下のパラメータで変換処理した際に得られる緑色の線です。
変換窓の大きさ2^6=64点、使用する周波数数45点。
すなわち、私たちがオリジナルに課した結果としてのカーブの似顔絵を得ることができます ...
図からわかるように、先頭を末尾に置き換えても、本当の結果にはならないのです -。
そこで問題は、緑色の線で示した曲線の動きをどのように継続させるか...。
1.一体なぜ、近似のために取った64点が周期関数だと判断したのでしょうか？
2.高調波の数は、採取したサンプルの半分を超えてはならない。すなわち、周期を64分割して近似すると、最大で31番目の高調波となる
3. 非周期的な関数を用いて近似したため、周期の継続が一致せず、非現実的な結果となる。PFは周期関数にのみ有効で、それ以外はタンバリンゲームだと、すでに言われていますね。
0〜2*PI、2*PI〜4*PIと、同じ周期を2回取る必要があります。両者を用いてPFを生成し、高調波の振幅と位相が一致しているかどうかを比較します。そうでない場合は、関数が非周期的であることを意味し、サンプリング周期を増やすか減らす必要があります（減少または増加 - これは個々の高調波の位相シフトを見るためです）。
あとはタンバリンで踊るだけです。
0〜2*PI、2*PI〜4*PIの2つの同じ周期を取る必要がある。両者とも、PFを曲げ、高調波の振幅と位相が一致するかどうかを比較する必要がある。Noの場合、関数が非周期的であることを意味し、サンプリング周期を増加または減少させる必要がある（減少または増加は個々の高調波の位相シフトに依存する）。
これも原理的には「タンバリンダンス」なのだが、より「工夫」をしているに過ぎない。その結果、「よりきれいな」ストーリーになるのであって、それ以上ではない。
周期関数とは、任意のxに対して次の等式f(x)=f(x+T)が成り立つようなTが存在する関数である。そうすると、Tは関数f(x)の周期となる。
簡単に言えば、トレーダーは、Tが（連続する2つの期間の公倍数として）提案されたアルゴリズムに従って選択されたとき、同じサンプルサイズの3番目の期間が選択された値に対応する保証はありません（そして3番目は、外挿が行われるだけの期間である）。Tを選択するアルゴリズムに保証はない。
ところで、もし関数が周期的であるなら、なぜこのフーリエが必要なのでしょうか？誰も考えたことがないのでしょうか？ピリオドを見つけて値を代入するだけ、それだけです;)。もちろん、時代を見極めてタンバリンで踊らなければの話ですが...。
>> 頑張ってください。
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索
皆さん、こんにちは...。
フーリエ変換について質問があるのですが・・・。
フーリエ変換後、逆変換でハイパスフィルタリング。
変換の範囲外で結果の関数を計算し続けたい場合（例があれば）・・・。