Ho bisogno di interpolare una funzione con impostazioni arbitrarie, quindi ho scelto le spline.
Ho capito bene che otterrò interpolanti diverse in base al numero di punti del nodo, cos'altro posso variare?
E la seconda domanda, cosa è meglio scegliere per l'interpolazione dalla lista, se ho solo bisogno di costruire molte interpolazioni diverse della serie originale (la variazione è importante)
Quale sia meglio scegliere è una domanda molto difficile. Un approccio, chiamato minimizzazione empirica del rischio, è sviluppato nel libro di Wapnick Algorithms and Dependency Recovery Programs. 1972, sembra.
Quale sia la scelta migliore è una domanda molto difficile. Un approccio, chiamato minimizzazione del rischio empirico, è sviluppato nel libro di Wapnick "Algoritmi e programmi per la ricostruzione della dipendenza". Sembra essere il 1972.
La massimizzazione delle probabilità/minimizzazione del rischio empirico, per come la vedo io, è solo un nome generale per gli algoritmi corrispondenti. Non ho bisogno dell'algoritmo in sé, ho solo bisogno di modificare le curve, preferibilmente in modo rapido e variabile, con la possibilità di trovare valori interpolanti su nuovi punti (il pacchetto spline permette quest'ultimo).
La massimizzazione delle probabilità/minimizzazione del rischio empirico, per come la vedo io, è solo un nome generale per gli algoritmi corrispondenti. Non ho bisogno dell'algoritmo in sé, ho solo bisogno di modificare le curve, preferibilmente veloci e variabili, con possibilità di trovare valori interpolanti su nuovi punti (il pacchetto spline permette quest'ultimo)
Sia il metodo della massima verosimiglianza che la minimizzazione (ricordo, non empirica, ma media) del rischio sono nomi non di algoritmi, ma di modi di impostazione degli obiettivi nel problem setting. Se l'obiettivo è raggiungibile, dà luogo a qualche algoritmo che è necessariamente coerente con l'obiettivo, è un'implementazione del suo raggiungimento in casi particolari. Se non avete bisogno né di obiettivi né di algoritmi per raggiungerli, non si possono dare consigli per il compito di scegliere le funzioni interpolanti. Ti resta da scegliere come ti dice il tuo cuore...
Ho bisogno di interpolare una funzione con impostazioni arbitrarie, quindi ho scelto le spline.
Ho capito bene che otterrò interpolanti diverse in base al numero di punti del nodo, cos'altro posso variare?
E la seconda domanda, cosa dovrei selezionare per l'interpolazione dalla lista, se ho solo bisogno di costruire molte interpolazioni diverse della serie iniziale (la variabilità è importante)?
La cosa più preziosa per un trader non è l'interpolazione e non l'approssimazione, ma l'estrapolazione.
Le spline non sono adatte all'estrapolazione.
Ho una grande esperienza e comprensione nell'approssimazione-estrapolazione polinomiale. Meno esperto è Fourier.
L'estrapolazione con metodi polinomiali e di Fourier sono di natura completamente diversa. L'estrapolazione di Fourier può essere applicata solo al mercato piatto a causa della sua natura periodica (questa linea è una somma di sinusoidi di diversa frequenza, fase e ampiezza), e tende sempre a tornare indietro,mentre l'estrapolazione polinomiale, al contrario, è buona per il trend, poiché cerca sempre di "volare su" o giù a causa della sua natura di grado.
Pertanto, ha senso combinare questi due metodi per ottenere buoni risultati di estrapolazione.
L'approssimazione polinomiale è di particolare interesse per i programmatori perché questo tipo di approssimazione è molto ben ottimizzato e può essere calcolato molto rapidamente. Sono riuscito ad uscire dai cicli per il calcolo dei coefficienti.
È anche importante ricordare che tutti i tipi di approssimazione creano linee ridisegnabili con ogni nuovo punto. Solo il tracciante della linea di approssimazione non viene ridisegnato.
Un'approssimazione polinomiale ha solo una soluzione, al contrario di un'approssimazione di Fourier. Questo permette la creazione di diapositive uniche non ridisegnabili:
Capisco, anche indovinare a caso non è male. Quindi nessuno ha risolto problemi simili. Lo visualizzerò, vedrò.
Nessuno l'ha risolto - sbagliato. Tutti i metodi di interpolazione hanno la loro giustificazione teorica e di solito un obiettivo chiaro. Per esempio, il difetto cubico di due spline minimizza l'energia potenziale di flessione elastica di un righello che passa attraverso i chiodi piantati nella tavola ai nodi della spline. In questo modo, una curva liscia (difetto inferiore a 3) è stata ottenuta da una tabella di punti in un disegno con il profilo di una nave o di un'ala. Le stesse spline rappresentano la deflessione di una trave multi-supporto nella matematica resiliente. Molto spesso l'obiettivo è quello di minimizzare la somma delle deflessioni delle coordinate ai nodi di interpolazione. Per confrontare i risultati dell'interpolazione con diversi obiettivi si ha bisogno di un obiettivo generalizzante, un criterio che sia calcolabile per qualsiasi metodo di interpolazione. Si basa sul numero di coefficienti da determinare. Grosso modo, se un'approssimazione polinomiale con un aumento del grado polinomiale da 3 a 7 riduce la somma dei quadrati di deviazione del 20%, allora il grado 3 è più ragionevole del 7. L'analogo in radiotecnica, se non mi confondo, è la frequenza di taglio del filtro.
La cosa più preziosa per un trader non è l'interpolazione o l'approssimazione, ma l'estrapolazione.
Le spline non sono adatte all'estrapolazione.
Ho grande esperienza e comprensione nell'approssimazione-estrapolazione polinomiale. Meno esperienza - Fourier.
L'estrapolazione con metodi polinomiali e di Fourier sono di natura completamente diversa. L'estrapolazione di Fourier può essere applicata solo al mercato piatto a causa della sua natura periodica (questa linea è una somma di sinusoidi di diversa frequenza, fase e ampiezza), e tende sempre a tornare indietro,mentre l'estrapolazione polinomiale, al contrario, è buona per il trend, poiché cerca sempre di "volare su" o giù a causa della sua natura di grado.
Pertanto, ha senso combinare questi due metodi per ottenere buoni risultati di estrapolazione.
L'approssimazione polinomiale è di particolare interesse per i programmatori perché questo tipo di approssimazione è molto ben ottimizzato e può essere calcolato molto rapidamente. Sono riuscito ad uscire dai cicli per il calcolo dei coefficienti.
È anche importante ricordare che tutti i tipi di approssimazione creano linee ridisegnabili con ogni nuovo punto. Solo il tracciante della linea di approssimazione non viene ridisegnato.
Un'approssimazione polinomiale ha solo una soluzione, al contrario di un'approssimazione di Fourier. Questo permette la creazione di diapositive uniche non ridisegnabili:
Va bene. Non ho nulla da estrapolare, è l'interpolazione che è necessaria. Voglio dire che non ha senso fare una previsione sulla base di tale estrapolazione. È necessario che questa linea sia il più forte possibile, da un lato all'altro, come la vostra linea blu. E voglio essere in grado di ottenere una soluzione sui nuovi punti, sì (senza ricalcolare sulla base della formula esistente).
Quindi ho solo chiesto cosa è meglio usare - polinomi o spline o qualche sottospecie. E forse anche il decimo grado sarebbe divertente.
Nessuno l'ha risolto - è sbagliato. Tutti i metodi di interpolazione hanno la loro giustificazione teorica e di solito un obiettivo chiaro. Per esempio, il difetto cubico di due spline minimizza l'energia potenziale di flessione elastica di un righello che passa attraverso i chiodi piantati nella tavola ai nodi della spline. In questo modo, una curva liscia (difetto inferiore a 3) è stata ottenuta da una tabella di punti in un disegno con il profilo di una nave o di un'ala. Le stesse spline rappresentano la deflessione di una trave multi-supporto nella matematica resiliente. Molto spesso l'obiettivo è quello di minimizzare la somma delle deflessioni delle coordinate ai nodi di interpolazione. Per confrontare i risultati dell'interpolazione con diversi obiettivi si ha bisogno di un obiettivo generalizzante, un criterio che sia calcolabile per qualsiasi metodo di interpolazione. Si basa sul numero di coefficienti da determinare. Grosso modo, se un'approssimazione polinomiale con un aumento del grado polinomiale da 3 a 7 riduce la somma dei quadrati di deviazione del 20%, allora il grado 3 è più ragionevole del 7. L'analogo in radiotecnica, se non mi confondo, è la frequenza di taglio del filtro.
È solo che se comincio a cercare di spiegare tutto quello che ci farò, diventerà di nuovo lunga qualche pagina :) Avete bisogno di variazioni, diversi gradi di polinomi, numero di punti della griglia, ecc.
Va bene. Non ho nulla da estrapolare, è l'interpolazione che è necessaria. Nel senso che una previsione su una tale estrapolazione non ha senso farla dopo. È necessario che questa linea sia il più forte possibile, da un lato all'altro, come quella blu. E voglio essere in grado di ottenere una soluzione sui nuovi punti, sì (senza ricalcolare sulla base della formula esistente).
Quindi ho solo chiesto cosa è meglio usare - polinomi o spline o qualche sottospecie. E forse anche il decimo grado sarebbe bello.
Esattamente l'interpolazione? Sei sicuro? Non approssimazione? E non è ridisegnabile?
Non interpolerete ogni tick.
Se avete bisogno di interpolazione su nodi intermedi (nodi ZigZag per esempio) senza ridisegnare, allora il punto è dove sarà il nodo successivo.
Puoi creare uno ZigZag chiaro non ridisegnabile solo se hai una macchina del tempo. Non c'è modo di determinare senza una macchina del tempo che la barra attuale sia un estremo.
C'è qualcuno sul forum che periodicamente chiamo un "cassetto di coda".
Il punto è la coda di cavallo.
È un classico di questo genere - spostare la SMA a sinistra di mezzo periodo e finire di disegnare quei semiperiodi come per caso con un polinomio di qualche grado. Per esempiohttps://www.mql5.com/ru/forum/224374. Probabilmente l'avete già visto.
Si può fare un'interpolazione molto bella lungo gli estremi zigzag con le spline, ma bisogna capire chiaramente che tra gli ultimi due o tre nodi ci sarà un ridisegno. Non c'è modo senza di essa!
Se non viene ridisegnato, non è un'interpolazione, ma ciò che io chiamo una traccia della linea approssimativa (non un'interpolazione!).
A parte i polinomi, non vedo nulla di comprensibile finora.
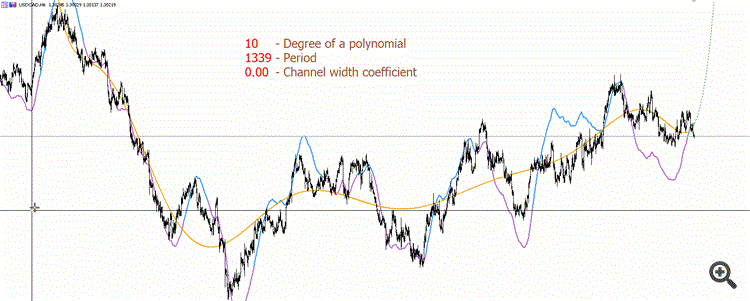
Ecco una gif appositamente registrata per dimostrare un esempio di polinomio di grado superiore (10), per capire quanto sia meno "bello" di quanto vorrei :))
La linea viola e blu non è ridisegnabile. Il viola è il polinomio che "guarda in basso", il blu è il polinomio che "guarda in alto".
E non c'è abbastanza precisione per calcolare polinomi di alto grado. Dovremo usare librerie speciali che utilizzano tipi di maggiore precisione. Il fatto che il "tracciatore" inizia a "saltare" a piccoli periodi nella gif - questa è la ragione per cui il doppio manca di precisione.
Ma personalmente non vedo alcun uso pratico per i polinomi di grado superiore a 5.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Ho bisogno di interpolare una funzione con impostazioni arbitrarie, quindi ho scelto le spline.
Ho capito bene che otterrò interpolanti diverse in base al numero di punti del nodo, cos'altro posso variare?
E la seconda domanda, cosa è meglio scegliere per l'interpolazione dalla lista, se ho solo bisogno di costruire molte interpolazioni diverse della serie originale (la variazione è importante)