Discussione sull’articolo "Modello di regressione universale per la previsione dei prezzi di mercato" - pagina 8
Ti stai perdendo delle opportunità di trading:
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Registrazione
Accedi
Accetti la politica del sito e le condizioni d’uso
Se non hai un account, registrati
Contattateci tramite messaggio privato per conoscere i termini e le condizioni.
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
Gli indicatori sono pagati o altro? Pubblicati nella base di codice, usateli a vostro piacimento!
Pubblicato un nuovo articolo Modello di regressione universale per la previsione dei prezzi di mercato:
Autore: Юсуфходжа
buon articolo.
molto impressionante
È un peccato, ma ci sono degli errori proprio all'inizio dell'articolo.
In primo luogo, l'incremento di prezzo in un certo momento t avrà ovviamente un valore e lo indichiamo con D0. Supponiamo che.
Poi... Ora, a t=0, capisco che non c'è alcun impatto sul prezzo e apparentemente non c'è nemmeno un incremento di prezzo dovuto all'impatto esterno. Tuttavia, abbiamo nuovamente chiamato il delta D0.
Poi abbiamo inserito dt/tau nella formula, che è comunque 1/C^2, cioè abbiamo dato un'accelerazione all'impatto, che muoverà comunque la regressione geometrica. Perché dovremmo? Dopo tutto, non abbiamo ancora definito che cosa sia questo impatto...
beh, in generale.
È un peccato, ma ci sono degli errori proprio all'inizio dell'articolo.
In primo luogo, l'incremento di prezzo in un certo momento t avrà ovviamente un valore e lo indichiamo con D0. Supponiamo che.
Poi... Ora, a t=0, capisco che non c'è alcun impatto sul prezzo e apparentemente non c'è nemmeno un incremento di prezzo dovuto all'impatto esterno. Tuttavia, abbiamo nuovamente chiamato il delta D0.
Poi abbiamo inserito dt/tau nella formula, che è comunque 1/C^2, cioè abbiamo dato un'accelerazione all'impatto, che muoverà comunque la regressione geometrica. Perché dovremmo? Dopo tutto, non abbiamo ancora definito che cosa sia questo impatto...
beh, in generale...
1. Do non è l'incremento del prezzo, ma il potenziale iniziale della forza che influisce sul prezzo al tempo t=0.
2. Dall'articolo: ".... assumiamo che il prezzo di mercato, che è in equilibrio, possa cambiare solo sotto l'azione di una forza esterna D(t), la cui entità e valore misureremo nella stessa dimensione del prezzo.
Supponiamo inoltre che la variazione del prezzo di mercato P(t) con il passare del tempo t dall'inizio dell'influenza di questa forza, aumentando continuamente dal valore zero per qualche regolarità a noi ancora sconosciuta, tenda a raggiungere il valore P(∞) = D0 all'infinito. In altre parole, con D0 intendiamo un aumento o una diminuzione finita del prezzo di mercato, a seconda della natura e del segno di questa forza d'influenza.
Inoltre, assumiamo che D(t=0) = D0. Supponiamo inoltre che durante l'infinitesimo periodo di tempo dt la forza d'influenza diminuisca del valore dD(t) in proporzione alla forza rimanente D(t) al momento t:
Da qui si ottiene la dipendenza esponenziale di D(t) dal tempo t nella forma:
Dove: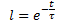
t - tempo dall'inizio dell'impatto della forza destabilizzante in unità di serie temporale, sec. (min, ore, giorni, settimane, decenni, mesi, anni);
τ (tau) - il coefficiente di proporzionalità, numericamente uguale alla costante di tempo del processo, sec.(min, ore, giorni, settimane, decenni, mesi, anni)".
Dove ha trovato la dimensionalità di 1/s^2? Quel rapporto non ha alcuna dimensionalità. Non l'ho inserito, ho ipotizzato che il tasso di variazione (diminuzione) di una forza che agisce su un processo sia proporzionale alla forza stessa, il che non contraddice la logica, e poi questa ipotesi è stata pienamente confermata. Come coefficiente di proporzionalità e introdotto il rapporto a (alfa) = 1/tau, che ha l'inverso del tempo, la dimensione. Per a (alfa) intendo l'impedenza del sistema, cioè la resistenza del sistema al flusso del processo, e tau è l'immagine del tempo nelle trasformazioni di Laplace, come si è scoperto in seguito, e permette di portare l'analisi del processo dal dominio differenziale a quello ordinario. Questo significa che ogni processo ha un suo tempo, diverso dal nostro, e tau funge da "traduttore" dei tempi, se così si può dire. Nelle viscere dell'articolo ho fornito un modo per stimare tau:
Ora, se sono noti i valori della funzione f ai corrispondenti istanti di tempo t, allora da questa equazione i parametri n, τ e il coefficiente β si determinano come segue:
dove:
I valori della funzione f ai corrispondenti istanti di tempo t e t sono determinati dai valori effettivi del prezzo di mercato P0, P1,..., Pk agli istanti di tempo h0, h1,..., һk dall'inizio della sua destabilizzazione mediante differenziazione numerica, riferita alla metà dell'intervallo:
f1 = (P1 - P0)/(ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); e così via;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; e così via.