В статье есть одно серьёзное противоречие. С одной стороны, мы установили с помощью индикатора трендовости, что реальной курс – трендовый. С другой стороны, мы утверждаем, что реальный курс колеблется в границах горизонтального фундаментального канала. А горизонтальный канал – очень сильный признак антитрендовости.
Non c'è alcuna contraddizione. La legge fondamentale della domanda-offerta prevede questi effetti. Il punto è questo: l'intero modello deve essere considerato in modo dinamico, cioè i confini del canale fondamentale orizzontale cambiano nel tempo. Per capire di cosa sto parlando, è necessario considerare prima un classico modello statico di domanda-offerta (per il "qui e ora"):
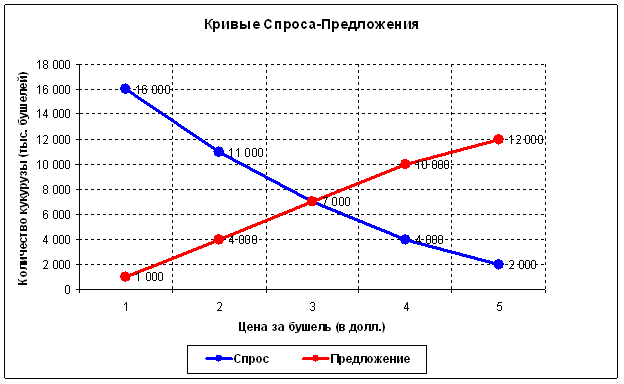
Cioè, in ogni momento, esiste un solo punto di scambio massimamente efficiente di un bene (in questo caso, 7000 bushel al prezzo di 3 dollari). In tutti gli altri punti, si scambieranno meno beni per meno denaro. La situazione macroeconomica cambia continuamente, il che significa che anche questo punto di scambio efficiente cambia. Tuttavia, il mercato è efficiente e il suo compito principale è quello di cercare costantemente questo punto o il prezzo di equilibrio ("tutti quelli che volevano comprare - hanno comprato, tutti quelli che volevano vendere - hanno venduto"). Il volume in questo punto dovrebbe essere grande, perché in questo punto viene scambiata la massima quantità di beni. Il mercato ha bisogno di tempo per realizzare un tale volume. Questa teoria prevede l'effetto dell'accumulo di volume:
Il mercato si trova per la maggior parte del tempo nella fase di consolidamento (nell'area della sua massima efficienza).
Tuttavia, l'economia mondiale nel suo complesso è in continua evoluzione. Emergono nuove tecnologie, il tenore di vita migliora. Di conseguenza, da un lato sono richiesti sempre più beni e servizi, dall'altro il progresso scientifico e tecnologico consente di produrre sempre più beni e servizi. La liquidità aumenta nel tempo. Il volume dei mercati mondiali deve crescere e, di conseguenza, aumenta la loro volatilità, con conseguente crollo delle crisi. Con l'aumento della domanda nel tempo, il prezzo aumenta. Allo stesso tempo, il progresso scientifico e tecnologico fornisce a questa domanda sempre più beni e servizi. Di conseguenza, il punto di equilibrio si sposta generalmente verso l'alto e verso destra nel corso del tempo. Anche il mercato, che si aggira costantemente intorno a questo punto, generalmente crescerà (tendendo a prezzi elevati).

Ecco da dove deriva questo "effetto di tendenza". La somma dei calcoli matematici è tale da lasciare senza fiato. In ogni caso, gli effetti economici dovrebbero spiegare le dipendenze matematiche, ma non il contrario.
C'è un'imprecisione nell'articolo: se prendiamo come analogia un marinaio ubriaco, la dimensione del passo è diversa. Grosso modo 1 passo è lungo 80 cm se si sposta dal pub, il passo indietro (verso il pub) 60 cm. La tendenza è la stessa, è anche noto che il movimento al ribasso del mercato è più veloce di quello al rialzo. E nell'articolo tutti i passi sono gli stessi, +1 o -1.
Quindi questo modello non può essere considerato adeguato. Si tratta solo di una moneta, le cui proprietà di distribuzione sono note e studiate da tempo.
c'è un'imprecisione nell'articolo: se prendiamo come analogia il marinaio ubriaco, la dimensione del passo è diversa. Grosso modo 1 passo è lungo 80 cm se ci si sposta dal pub, il passo indietro (verso il pub) 60 cm. La tendenza è la stessa, è anche noto che il movimento al ribasso del mercato è più veloce di quello al rialzo. E nell'articolo tutti i passi sono uguali, +1 o -1".
La moneta ha un analogo continuo: il modello del moto browniano geometrico. È descritto qui http://algoritmus.ru/?p=2889.
"Approccio stocastico alla soluzione di problemi di trading algoritmico".
Autori: Arsen Yakovlev, Grigory Franguridi
Pubblicato: rivista "D-Shtrich" #16/6 settembre 2010
Questo articolo ha le stesse idee del mio, solo più matematica. Se prendere un modello discreto o continuo è una questione di gusti. Sono uguali. Solo che un modello ha gli integrali e l'altro le somme. E il modello a moneta è già compreso dai ragazzi delle scuole, mentre il modello continuo è compreso solo dagli studenti.
"È anche noto che il movimento al ribasso del mercato è più veloce di quello al rialzo" - questo è molto interessante per me - può darmi un link alla ricerca/articolo - mi serve per l'autoformazione.
"Quindi questo modello non può essere considerato adeguato in alcun modo. È solo una moneta le cui proprietà di distribuzione sono note e studiate da tempo". - Nessun modello descrive adeguatamente la realtà al 100%. Compreso il tasso della moneta come modello di mercato. Ecco perché abbiamo dovuto inventare un modello di moneta con un trend per essere più adeguato al mercato.
- 2010.09.13
- val
- algoritmus.ru
Perché proprio una moneta? Ha due facce: cosa riflettono? Solo un ideale vagare casuale su una linea retta (analogamente - su, giù), cioè monodimensionale. Il prezzo può avere un altro stato - piatto, cioè è già una moneta con tre lati, cioè abbiamo una camminata casuale bidimensionale. Dai grafici precedenti si può notare che tale stato del mercato non è praticamente modellato - non si vede un piatto rigido.
La curva gialla della Figura 2 è la più vicina a un piatto. Il piatto più stretto si ottiene se prendiamo il parametro a=-0,5. Allora otterremo una linea orizzontale +1 -1 +1 -1 +1 -1 +1 -1 Allora otterremo una linea orizzontale +1 -1 +1 -1 -1 +1 -1 -1 ..... Quindi due facce della medaglia sono sufficienti per descrivere un piatto. A proposito, "piatto" in termini di articolo è chiamato "anti-trend".
Ma allora l'intero grafico diventerà più orizzontale, se ho capito bene, e nel mercato reale ci possono essere sia una tendenza netta che una piatta, vale a dire che questi fenomeni sono indipendenti. L'indipendenza è la necessità di una terza faccia della medaglia. Semplicemente, il mercato sta vagando sul piano, perché il fattore tempo vaga, e la moneta ha un modello unidimensionale di vagabondaggio, e un semplice (senza vagabondaggio) sweep di questo modello per il tempo non è del tutto corretto. Ma nonostante questo l'articolo è molto utile.
Esattamente, nel modello della moneta con un trend, la tendenza è considerata costante per tutta la durata del mercato. E come mostra l'indicatore di trendiness sul tasso reale, il trendiness cambia continuamente. E solo in media su un lungo periodo di tempo (anni) la trendiness viene misurata come costante.
Per far sì che il modello "tasso di moneta con tendenza" corrisponda al mercato, è possibile complicarlo. Il parametro "a" può essere reso caoticamente dipendente dal tempo o si può inventare qualcos'altro. È una cosa creativa. A rigore, non è necessario introdurre una seconda dimensione, ma se si vuole, si può aggiungere un secondo moltiplicatore caotico accanto ad "a".
Per testare, ad esempio, questo indicatore New Moving Mini-Max di analisi tecnica e la sua implementazione in MQL5, è necessario un modello semplice con una tendenza costante . Non è realistico trattare un indicatore di questo tipo sul corso reale, ma sarebbe bello testarlo su un modello semplice con una tendenza costante.
...Scegliere un modello discreto o continuo è una questione di gusti. Sono uguali. Solo che un modello ha degli integrali e l'altro delle somme. E il modello a moneta è già compreso dai ragazzi delle scuole, mentre quello continuo solo dagli studenti...
è qui che sta l'errore.
1. Il passaggio dal modello continuo al modello discreto deve essere fatto correttamente.
2. I due modelli possono essere uguali (continuo e discreto), ma è necessario soddisfare la condizione che il passo in + e in - deve essere lo stesso. La sua entità.
3. si sono prese delle barre per analizzare, che la vostra affermazione sarebbe vera "Sono gli stessi". Solo un modello ha gli integrali e l'altro le somme". Dimostrate che tutte le barre sono uguali. Potete dimostrarlo?
4. solo un grafico ha questa proprietà, il grafico renko... puoi sostituirlo con +1 -1(https://www.mql5.com/it/code/9447#25419).
Grazie per il link all'articolo. L'ho letto. Suggerisce di utilizzare il modello ARFIMA, il random walk. Si tratta di modelli diversi. Sarebbe interessante leggere il seguente articolo, sia il suo che quello dell'autore. Dove si dimostra che i modelli di mercato da voi proposti sono adeguati. Non solo asserito a parole, ma dimostrato matematicamente ... e dato il calcolo di questa cifra...
H.Y. Solo molte persone afferrano questa bella parola adeguatezza, ma come calcolarla non lo sanno nemmeno loro. Nel tuo post hai scritto che un modello adeguato al 100% non esiste. Sono assolutamente d'accordo con lei. La domanda è quanto il modello proposto sia adeguato al mercato del 20, 30 o 99,999999999%....
Provate a modellare una pila, la pila ha una struttura chiara, la pila vede ordini per un certo numero di punti in alto e in basso.
Il generatore passa attraverso tutte le celle (non può essere +1 -1 ma la generazione di volumi casuali), quindi dopo che tutte le celle della pila sono passate dal generatore, viene effettuato il calcolo di dove spostare il punto centrale della pila.
Non dimenticate di riavviare SRAND dopo aver generato 32768 rand, altrimenti la sequenza si ripeterà.
- App di trading gratuite
- Oltre 8.000 segnali per il copy trading
- Notizie economiche per esplorare i mercati finanziari
Accetti la politica del sito e le condizioni d’uso
Il nuovo articolo Random Walk e l'indicatore di tendenza è stato pubblicato:
Random Walk sembra molto simile ai dati di mercato reali, ma ha alcune caratteristiche significative. In questo articolo considereremo le proprietà di Random Walk, simulato utilizzando il gioco del lancio della moneta. Per studiare le proprietà dei dati, viene sviluppato l'indicatore di tendenza.
Per cominciare, simuliamo il risultato del gioco del lancio della moneta utilizzando un generatore di numeri casuali. Quindi, facciamo che le teste siano un +,1 e le croci siano -1. Il risultato dell'i-esimo lancio della moneta è x (i) = p (1/2), dove p (1/2) è una funzione che prende i valori +1 con la probabilità di 1/2 e il valore -1 con la stessa probabilità 1/2.
Quindi la Random Walk sarà semplicemente la somma di x(i). Per semplicità, partiamo da zero.
Figura 1. Random Walk: (asse verticale - posizione corrente sulla linea, dall'asse orizzontale - passaggi temporali)
Autore: Гребенев Вячеслав