Vous manquez des opportunités de trading :
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Inscription
Se connecter
Vous acceptez la politique du site Web et les conditions d'utilisation
Si vous n'avez pas de compte, veuillez vous inscrire
Non, non. Pas faux. Voici la dépendance du montant du retrait, qui découle de la formule itérative (en rouge), et de la dépendance analytique (en bleu).
Vous pouvez voir qu'ils coïncident et qu'il y a un maximum en k (sur la page précédente du sujet).
En clair, il ne s'agit pas de retraits discrets mais nécessairement de retraits continus à parts égales. Il n'y a donc pas de solution pour effectuer des retraits différents selon les périodes. Il n'y a donc pas de solution pour retirer tout à la fin sans retirer avant. Cela ne découle pas des conditions du problème, mais des formules que vous appliquez (k est fixe, pas variable ki, i=0...T)
Total des fonds retirés
l'effet devient tangible si le taux de croissance est suffisamment élevé
J'ai des dépendances similaires.
J'essaie maintenant de décomposer l'expression de la dérivée en puissances de k, mais cela ne sert à rien - je dois tenir six ordres de grandeur. Il est clair que cela ne peut pas être résolu analytiquement. Peut-être y a-t-il d'autres idées ? Quelqu'un a mentionné les diphurcs...
J'ai des dépendances similaires.
J'essaie maintenant de décomposer l'expression de la dérivée en puissances de k, mais cela ne sert à rien - je dois tenir six ordres de grandeur. Il est clair que cela ne peut pas être résolu analytiquement. Peut-être y a-t-il d'autres idées ? Quelqu'un a mentionné les diphurcs...
C'est un peu compliqué d'un point de vue analytique. Sur q et t. Cela dépend en quelque sorte d'une manière délicate :) Au fur et à mesure que q augmente, la fraction de l'enlèvement optimal diminue de façon constante lorsque t augmente.
J'ai des dépendances similaires.
J'essaie maintenant de décomposer l'expression de la dérivée en puissances de k, mais cela ne sert à rien - je dois tenir six ordres de grandeur. Il est clair que cela ne peut pas être résolu analytiquement. Peut-être y a-t-il d'autres idées ? Quelqu'un a mentionné les diphurcs...
Vous pouvez passer du particulier au général. Par exemple, si t = 1, vous ne pouvez retirer de l'argent qu'une seule fois, et vous devez donc retirer un montant de q. On considère ensuite le cas pour t = 2, t = 3, etc.
C'est-à-dire que si à t = 2 il est optimal de retirer moins de q à la fois, alors trouver un extremum et généraliser pour tous les q à t = 2.
De même pour t = 3, t = 4, etc.
A partir de la valeur de l'extremum, il sera possible d'obtenir la taille du retrait comme f(t)
On peut envisager un schéma de vaisseaux connectés pour constituer le DU.
Volume initial du premier vaisseau B0
Vous pouvez passer du particulier au général. Par exemple, si t = 1, vous ne pouvez retirer de l'argent qu'une seule fois, et vous devez donc le retirer pour un montant de q. On considère ensuite le cas pour t = 2, t = 3, etc.
A partir de la valeur de l'extremum, nous pourrons obtenir la taille du retrait comme f(t)
Vous avez peut-être raison. Sauf que pour t = 3 nous avons déjà selon l'équation le degré k - trois dans la dérivée première df(k)/dk=0, et nous devons chercher les racines de l'équation cubique avec tout ce que cela implique... C'est-à-dire que nous ne pouvons pas aller plus loin que t=3 dans ce scénario. Rappelons que
le degré k - trois dans la dérivée première df(k)/dk=0, et nous devons chercher les racines de l'équation cubique avec tout ce que cela implique... C'est-à-dire que nous ne pouvons pas aller plus loin que t=3 dans ce scénario. Rappelons que 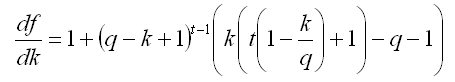 , et pour t=1 la taille optimale k=q, pour t=2 k=q, pour t=3 k=q. Mais augmenter encore t et résoudre de manière analytique ne fonctionnera pas. Si vous le résolvez numériquement, vous pouvez voir que si le taux de croissance des dépôts q est de 10 % par mois, le taux de retrait optimal devient inférieur à q à t>30 mois.
, et pour t=1 la taille optimale k=q, pour t=2 k=q, pour t=3 k=q. Mais augmenter encore t et résoudre de manière analytique ne fonctionnera pas. Si vous le résolvez numériquement, vous pouvez voir que si le taux de croissance des dépôts q est de 10 % par mois, le taux de retrait optimal devient inférieur à q à t>30 mois.
La conclusion s'ensuit : si la fiabilité du TS est telle que la durée de vie moyenne du dépôt ne dépasse pas 3 ans, alors le comportement optimal est un retrait mensuel de tout le bénéfice gagné (le dépôt ne croît pas). Sinon, nous devons trouver une solution analytique pour le pourcentage de retrait optimal k et agir selon la formule. Ce scénario garantit un maximum d'argent de poche pendant la durée de vie prévue du dépôt.
Afin de réaliser le DU, nous pouvons considérer le schéma des vaisseaux connectés.volume initial du premier vaisseau B0
Si les vaisseaux (flux de fluide) sont en équilibre dynamique (c'est-à-dire qu'il y a autant de fluide par unité de temps qui entre dans le premier vaisseau que de fluide qui sort du dernier), le problème du niveau d'eau dans chaque vaisseau est résolu de manière élémentaire et ne se réduit pas au problème du dépôt. Si l'on considère les navires en cours de remplissage, l'analogie avec le dépôt n'est pas évidente. avtomat ,expliquez, s'il vous plaît, ce que vous vouliez dire en proposant une telle interprétation ?
P.S. L'appel à obtenir une solution analytique approximative de l'équation df/dk=0 est toujours valable. Toutes les idées sont les bienvenues.