Discussion de l'article "Utiliser l'Analyse Discriminante pour Élaborer des Systèmes de Trading"
A l'auteur (pas de pseudo pour une raison quelconque).
Le même problème peut être résolu d'une autre manière. Il existe des tests pour les variables redondantes et manquantes. Je pourrais le faire et comparer avec vos résultats. Mais j'ai besoin de tous vos fichiers au format .csv.
...J'ai besoin de tous vos fichiers au format .csv.
Je pense que la source se trouve dans l'archive masterdata.zip.
Article publié Utiliser l'analyse discriminante pour construire des systèmes de trading:
Auteur : ArtemGaleev
Après avoir choisi les variables, nous devrons établir une relation entre elles, dans laquelle le prix sera la variable dépendante (fonction) et les autres indicateurs seront les variables indépendantes. Voici l'équation schématique :
prix prix(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 signifie la valeur précédente. Ceci est naturel puisque l'indicateur est dérivé du prix de manière analytique. Prenons en compte le fait que le prix est un incrément, nous prendrons donc les incréments des indicateurs. Par paresse, je ne prends pas tous les indicateurs. Estimons cette équation par la méthode des moindres carrés :
Nous avons obtenu une estimation des coefficients de l'équation. La dernière colonne est très intéressante : il s'agit de la probabilité que le coefficient correspondant soit égal à zéro. Cette probabilité pour tous les coefficients est largement supérieure à au moins 10%, c'est-à-dire que l'on peut considérer que l'on ne peut pas rejeter l'hypothèse que les coefficients correspondants sont égaux à zéro. En conséquence, le R au carré a une valeur ridicule.
J'en conclus qu'il est inutile de s'occuper de la classification des indicateurs - ils sont inutiles parce qu'ils n'ont rien à voir avec l'augmentation des prix.
Ou est-ce que je me trompe ?
...Ou ai-je tort ?
Je pense que vous avez raison :-)
faa1947, j'ai une question à vous poser. Je voulais clarifier quelques points... Voici comment j'ai calculé les données de votre équation :
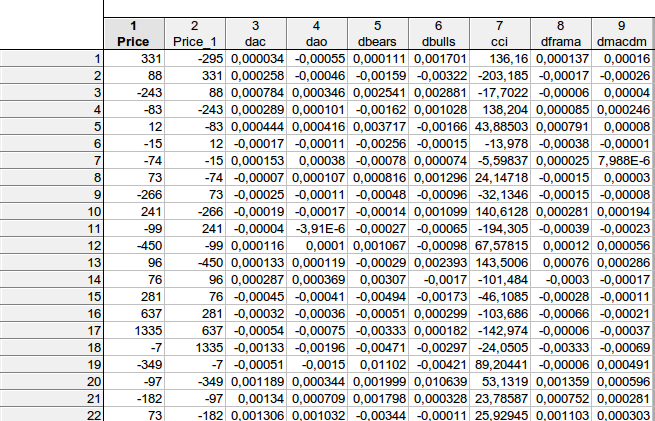
Les données du tableau correspondent-elles à votre équation schématique price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
Et j'ai obtenu le résultat suivant :
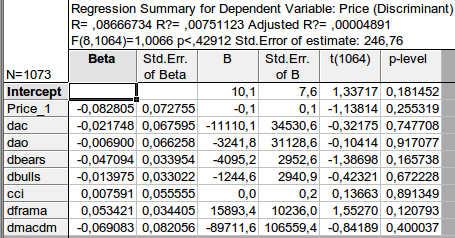
Une fois que nous avons choisi les variables, nous devons établir une relation entre elles, dans laquelle le prix sera la variable dépendante (fonction) et les autres indicateurs seront les variables indépendantes. Voici une équation schématique :
prix prix(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)
-1 signifie la valeur précédente. Ceci est naturel puisque l'indicateur est dérivé du prix de manière analytique. Prenons en compte le fait que le prix est un incrément, nous prendrons donc les incréments des indicateurs. Par paresse, je ne prends pas tous les indicateurs. Estimons cette équation par la méthode des moindres carrés :
Nous avons obtenu une estimation des coefficients de l'équation. La dernière colonne est très intéressante : il s'agit de la probabilité que le coefficient correspondant soit égal à zéro. Cette probabilité pour tous les coefficients est largement supérieure à au moins 10%, c'est-à-dire que l'on peut considérer que l'on ne peut pas rejeter l'hypothèse que les coefficients correspondants sont égaux à zéro. En conséquence, le R au carré a une valeur ridicule.
J'en conclus qu'il est inutile de s'occuper de la classification des indicateurs - ils sont inutiles parce qu'ils n'ont rien à voir avec l'augmentation des prix.
Ai-je tort ?
Veuillez indiquer le nom de la méthode statistique que vous avez utilisée. Il s'agit de la construction d'une équation de régression linéaire, dans laquelle les indicateurs constituent l'entrée et le prix futur la sortie ? Est-ce exact ? Cette méthode ne fonctionne pas pour le forex car il ne s'agit pas d'un système déterministe linéaire. L'analyse discriminante a une tâche différente, elle construit des modèles pour la reconnaissance de modèles basés sur des descriptions externes du système.
Si la classification des indicateurs pour analyser les incréments de prix était inutile, l'analyse technique n'aurait aucun sens. Heureusement, le prix ne se comporte pas de manière chaotique, il a une mémoire des événements précédents.
Vous semblez avoir raison :-)
faa1947, j'ai une question à vous poser. Je voulais clarifier quelques points... Voici comment j'ai calculé les données de votre équation :
Les données du tableau correspondent-elles à votre équation schématique price price(-1) dac(-1) dao(-1) dbears(-1) dbulls(-1) cci(-1) dframa(-1) dmacdm(-1)?
Et j'ai obtenu le résultat suivant :
Les données brutes se présentent comme suit :
Les équations se présentent comme suit :
Equation d'estimation :
=========================
PRIX = C(1)*PRIX(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
Coefficients substitués :
=========================
PRIX = -0.0228102658125*PRIX(-1) + 12005.8974278*DAC(-1) + 4033.10946937*DAO(-1) + 3176.11232129*DBEARS(-1) - 6021.36196728*DBULLS(-1) - 0.102710105369*CCI(-1) - 11487.4273249*DFRAMA(-1) + 62535.3387412*DMACDM(-1)
Je ne comprends pas votre calcul. J'ai pour principe d'utiliser la valeur lag (valeur précédente). Cela permet de faire une prédiction. Si le lag -1 correspond à la 1ère observation, alors la variable dépendante correspond à une nouvelle observation non observée, prédite.
Qu'est-ce que le niveau p ? Pour moi, c'est la probabilité que le coefficient correspondant soit nul.
Veuillez indiquer le nom de la méthode statistique que vous avez utilisée. S'agit-il d'une équation de régression linéaire dans laquelle les indicateurs constituent l'entrée et le prix futur la sortie ? Est-ce exact ?
La régression a été estimée à l'aide de la méthode des moindres carrés. Elle peut être utilisée pour faire des prédictions.
Cela ne fonctionnera pas pour le forex car il ne s'agit pas d'un système déterministe linéaire.
S'il est linéaire, c'est dans un exemple spécifique. Il n'est pas déterministe car même les coefficients sont traités comme des variables aléatoires. Tous les coefficients ne sont pas calculés, mais estimés. La deuxième colonne indique l'erreur standard de l'estimation des coefficients. Veuillez noter qu'elle est énorme.
Si la classification des indicateurs permettant d'analyser les hausses de prix était inutile, l'analyse technique n'aurait aucun sens.
Exactement, et j'ose vous assurer que je ne suis pas le seul à le penser. L'AT n'est pas une science, mais une sorte d'astrologie. A l'origine, il y a 300 ans, il s'agissait d'un système de visualisation du kotir. Elle a énormément évolué depuis. Tout le reste est pour les Pinocchios dans le domaine des miracles. J'ai été satisfait de votre article, car il contient des réflexions régulières et reproductibles.
Si la classification des indicateurs pour l'analyse de la hausse des prix était inutile
Nous avonsici analysé un cas particulier d'indicateurs. Il est toujours nécessaire de prouver qu'un indicateur particulier ou son utilisation a quelque chose à voir avec une cotation. L'AT ne prend jamais en compte cette question.
Heureusement, le prix ne se comporte pas de manière chaotique, il a une mémoire des événements précédents.
Toute l'économétrie repose sur l'hypothèse qu'une cotation a une composante déterministe (autocorrélation, mémoire) et du bruit.
L'analyse discriminante a une tâche différente : elle construit des modèles pour la reconnaissance des formes sur la base de descriptions externes du système.
La tâche est claire. Mais la question est de savoir si l'on peut se fier au résultat obtenu. Le problème n'est pas la classification (c'est une partie du problème, qui doit également être résolue), mais la confiance dans la prédiction obtenue. C'est exactement le problème.
Je ne comprends pas votre calcul. Mon principe est d'utiliser la valeur lag (valeur précédente). Cela permet de faire une prédiction. Si le décalage -1 correspond à la première observation, alors la variable dépendante correspond à une nouvelle observation non observée, prédite.
Qu'est-ce que le niveau p ? Pour moi, c'est la probabilité que le coefficient correspondant soit nul.
faa1947, j'ai donné le tableau avec les retards (pour les premières lignes - je ne peux pas ajuster le tableau entier). Mais j'ai d'abord calculé les différences d'indicateurs, de sorte que le nombre total de lignes est de 1073 au lieu de 1074. Ensuite, j'ai avancé la variable dépendante Price d'un pas.
Il s'est avéré que, dans l'exemple de la première ligne :
331 = C(1)*(-295) + C(2)* 0.000034+ C(3)* (-0.00055) + C(4)* 0.000111 + C(5)* 0.001701+ C(6)*136.16+ C(7)* 0.000137+ C(8)*0.00016, à condition que
PRIX = C(1)*PRIX(-1) + C(2)*DAC(-1) + C(3)*DAO(-1) + C(4)*DBEARS(-1) + C(5)*DBULLS(-1) + C(6)*CCI(-1) + C(7)*DFRAMA(-1) + C(8)*DMACDM(-1)
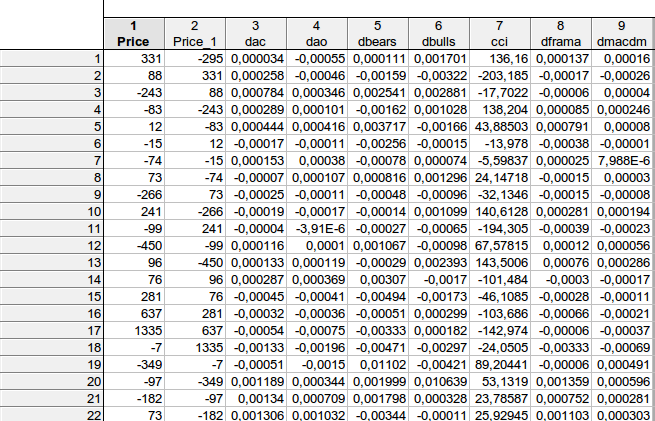
En général, j'ai obtenu approximativement un résultat similaire - il n'y a aucun moyen de rejeter l' hypothèse nulle que les coefficients considérés sont égaux à zéro...
- Applications de trading gratuites
- Plus de 8 000 signaux à copier
- Actualités économiques pour explorer les marchés financiers
Vous acceptez la politique du site Web et les conditions d'utilisation
Un nouvel article Utiliser l'Analyse Discriminante pour Élaborer des Systèmes de Trading a été publié :
Lors de l’élaboration d'un système de trading, il se pose généralement un problème de sélection de la meilleure combinaison d'indicateurs et de leurs signaux. L'analyse discriminante est l'une des méthodes pour trouver de telles combinaisons. L'article donne un exemple d’élaboration d'une évaluation environnementale pour la collecte de données de marché et illustre l'utilisation de l'analyse discriminante pour la construction de modèles prognostiques pour le marché FOREX dans le logiciel Statistica.
Pour ouvrir le fichier dans Statistica, procédez comme suit.
Fig. 1. Importation du fichier dans Statistica
Auteur : ArtemGaleev