Discusión sobre el artículo "Características del Wizard MQL5 que debe conocer (Parte 11): Muros numéricos"
¿Puede comprobar esta tabla?
Si intento repetirlo obtengo resultados diferentes:
| Fila 0 | 0 | 0 | 0 | 0 |
| Fila 1 | 1 | 1 | 1 | 1 |
| Fila 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Fila 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
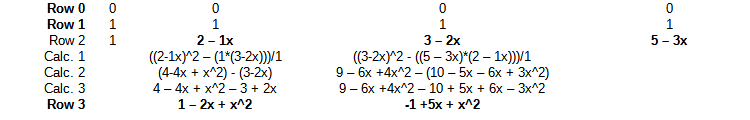
¿Puede comprobar esta tabla?
Si intento repetirlo obtengo resultados diferentes:
| Fila 0 | 0 | 0 | 0 | 0 |
| Fila 1 | 1 | 1 | 1 | 1 |
| Fila 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Fila 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
Hola,
Acabo de ver esto. Déjame echar un vistazo y revertir.
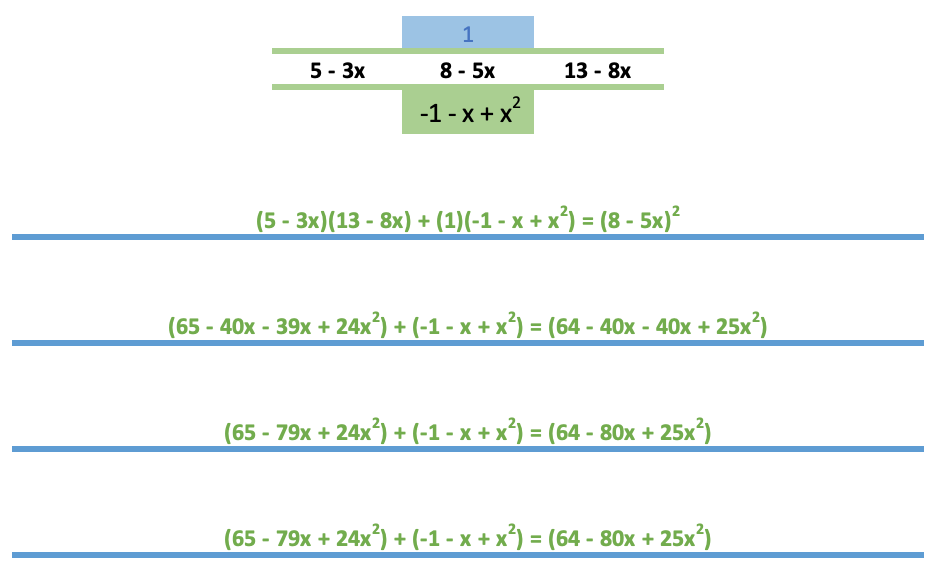
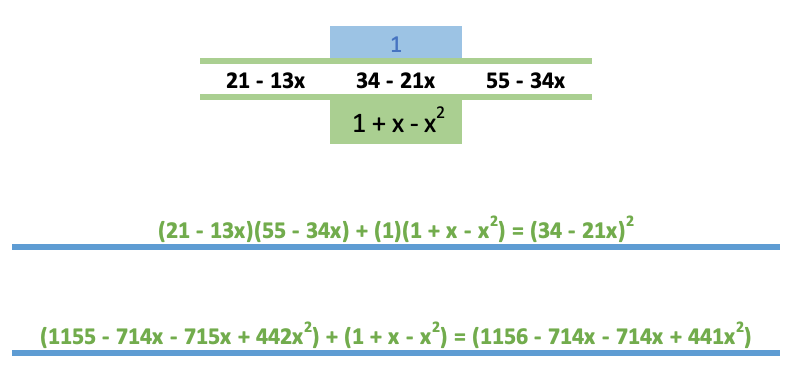
Pse ver más abajo:
Así no es como se demuestran las identidades pero creo que el álgebra está bien.
Pse ver más abajo:
Así no es como se demuestran las identidades pero creo que el álgebra está bien.
Lo siento no :(
Parece que tu ejemplo es el único que funciona (¿realmente necesitas este ejemplo?), mira aquí.
| Fila 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Fila 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Fila 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x | 8 - 5x | 13 - 8x | 31 - 13x |
| Calc. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | (5 - 3x)^2 - ((3 - 2x)(8 - 5x)) | (8 - 5x)^2 - (5 - 3x)(13 - 8x) | (13 - 8x)^2 - ( (8 - 5x)(31 - 13x) ) | ||
| Calc. 2 | (4 - 4x + x^2) - (3 - 2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | 25 - 30x + 9x^2 - (24 - 15x +16x + 10x^2) | 64 - 80x +25x^2 - (65 - 39x - 40x + 24x) | 169 - 208x + 64x^2 - (248 - 104x - 155x + 65x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | 25 - 30x + 9x^2 - 24 + 15x - 16x - 10x^2) | 64 - 80x +25x^2 - 65 + 39x + 40x - 24x) | 169 - 208x + 64x^2 - 248 + 104x + 155x - 65x^2) | ||
| Fila 3 | 1 - 2x + x^2 | -1 +5x + x^2 | 1 - 31x - x^2 | -1 - 1x + x^2 | -79 - 51x - 1x^2 |
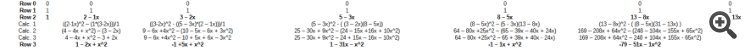
- mathworld.wolfram.com
Me gustaría revisarlos todos, pero ya me hago una idea...
Sí tienes razón excepto en el primer cálculo - quizás lo has elegido por desgracia.
Con 1 - 2x + x^2 que coincide con sus resultados alternativos de -1 -1x + x^2 y 1 +1x - x^2 :(
Sí, tienes razón, excepto en el primer cálculo, quizá lo hayas elegido por desgracia.
Con 1 - 2x + x^2 que coincide con sus resultados alternativos de -1 -1x + x^2 y 1 +1x - x^2 :(
Um, usted dijo que sólo uno coincide, así que lo que acabo de compartir fue un segundo que coincide.
Yo podría ir a través de todos, pero si usted sigue mi proceso anterior, usted debe obtener resultados similares en todos.
- 2024.01.31
- MetaQuotes
- www.mql5.com
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso
Artículo publicado Características del Wizard MQL5 que debe conocer (Parte 11): Muros numéricos:
Los muros numéricos (Number Walls) son una variante de los registros de desplazamiento lineal hacia atrás (Linear Shift Back Registers) que pre-evalúan las secuencias para su predictibilidad mediante la comprobación de la convergencia. Veamos cómo se pueden utilizar estas ideas en MQL5.
Para las series temporales múltiples, podemos derivar una fórmula para el siguiente valor de la secuencia basándonos en los valores anteriores que han aparecido en ella. Los muros numéricos lo consiguen creando primero un "muro numérico" en forma de matriz usando la llamada regla cruzada (cross-rule). Creando esta matriz, el objetivo principal será establecer si la secuencia considerada converge. El algoritmo de muro numérico de regla cruzada responde a esta pregunta si, tras unas filas de aplicación, las filas siguientes de la matriz son solo ceros.
En elartículo presentado, que demuestra estos conceptos, se utilizó la serie de potencias de Laurent (Laurent Power Series), también conocida como serie formal de Laurent (Formal Laurent Series, FLS), como base para representar estas secuencias con su aritmética en formato polinómico utilizando productos de Cauchy.
A continuación, le presentamos las pruebas comparativas de los asesores montados por el Wizard. Ambos utilizan las señales de Awesome Oscillator y tienen básicamente los mismos ajustes de entrada, que mostramos a continuación:
La diferencia entre los dos es que un asesor utiliza Parabolic SAR para rastrear y cerrar posiciones abiertas, mientras que el otro utiliza el algoritmo de muro numérico presentado en este artículo. Sin embargo, sus informes al realizar las pruebas con EURUSD durante el último año en el marco temporal de horas, a pesar de tener la misma señal, son diferentes.
Autor: Stephen Njuki