Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
No lo sé, tengo escrito cuál es la fórmula y todas las variables están definidas. Permítanme aclarar también que se trata de la cantidad de beneficios retirados cada mes (no el beneficio total de m meses).
Queda por derivar la fórmula para la suma de las series, usted escribió que lo hace fácilmente - hacerlo. Entonces toma la derivada, la iguala a cero...
En mis anotaciones, su fórmula para el retiro del mes actual se ve así:
En consecuencia, descomponer la derivada bestial de esta función es tan difícil como la anterior.
Creo que puedes intentar preprologaritmizar f y luego buscar su máximo... Tal vez sea más fácil así.
avtomat:
Y luego, en el segundo paso, abrir la válvula que divide el flujo en dos partes. Esto cambiará el flujo de entrada.
¿Aún no ves la solución?
No, no sé lo que estás pensando. Dígame.
Hay algunos que ni siquiera el teorema de Pitágoras, tal y como lo interpretan ellos, se puede entender.
OFFTOP:
En la escuela dieron la prueba más sucinta del teorema de Pitágoras.
Nota, la idea básica más simple (no estándar) es p.2. No se utiliza ningún conocimiento de las propiedades de los triángulos semejantes, tampoco se necesitan conocimientos de trigonometría para entender la existencia de la función f. Es decir, dicha prueba se puede dar en las escuelas primarias después de explicar bien (no como es habitual) a los niños lo que es el área.
OFFTOP:
En la escuela dieron la prueba más sucinta del teorema de Pitágoras.
¿En qué grado?
La fórmula S = c^2 * f(alfa) no es obvia para un alumno de 7º grado. Es dar por hecho que lo es.
En consecuencia, romper la derivada bestial de esta función es tan difícil como la anterior.
¿Está todo el proceso atascado con el derivado?
¿Es esta función x0*k*(1-(1+q-k)^2)/(k-q)?
Si es así, no hay problema, los he resuelto fácilmente, sólo hay que recordar un poco. La variable q?
¿en qué clase?
La fórmula S = c^2 * f(alfa) no es obvia para un alumno de 7º grado. Es dar por hecho que lo es.
Casi cualquier niño al que se le haya introducido el concepto de área de una figura lo suficientemente bien como para sentirlo tendrá pocas dificultades para entender la prueba anterior.
Si un niño entiende realmente lo que es el área, comprende la medida de la misma y también entiende que el área de cualquier figura se puede expresar a través de sus características (en este caso la hipotenusa y el ángulo) que definen de forma única la figura.
No es necesario conocer las propiedades de los triángulos semejantes ni la trigonometría.
Hace poco estuve de visita y vi dos pirámides de piedra (similares a las egipcias). Los tomé en mis manos y los puse en sus bases (son ligeramente diferentes en tamaño):
Y se le ocurrió otra demostración del teorema de Pitágoras (clara en la construcción).
Integer:
Весь процесс уперся в производную?
Вот эта функция - x0*k*(1-(1+q-k)^2)/(k-q)?
Если это так, то это как бы не проблема, я их легко решал, только вспомнить надо немного. Переменная q?
No, el problema es la derivada de k de: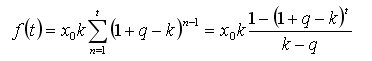
Hay que igualarlo a cero y resolverlo con respecto a k.
No puedo hacerlo de forma inteligente, así que lo haré sencillo:
Digamos que hay 10.000 en el depósito al principio del periodo. Cada periodo añadimos un 5% al depósito y lo reinvertimos en él. En cada periodo se nos permite retirar sólo el 3%.
Si se retira todo el 3% de su dinero en cada período, todo lo que obtenemos más de 4k $ (y no dan una mierda sobre el depósito), de lo contrario obtenemos sólo 0,5k $ (pero con mucho en el depósito).
Casi cualquier niño al que se le haya introducido el concepto de área de una figura lo suficientemente bien como para sentirlo tendrá pocas dificultades para entender la prueba anterior.
Si un niño entiende realmente lo que es el área, comprende su medida y también entiende que el área de cualquier figura puede expresarse a través de sus características (en este caso la hipotenusa y el ángulo), que definen de forma única la figura.
Pero no es una prueba rigurosa.
No puedo hacerlo de forma inteligente, así que lo haré sencillo:
Por eso necesitamos una solución analítica general, no para dibujar esas tablas, sino para sustituir dos valores de entrada en una fórmula sencilla y obtener la respuesta.
Esa es la cuestión, todo lo anterior es "parece que va a ser así". Que "puede expresarse de alguna manera a través de algo".
Pero no es una prueba rigurosa.
¡¿Qué clase de prueba contundente es esa?! Es evidente: