Arrendatario - página 6
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
No, no. No está mal. Aquí se muestra la dependencia de la cantidad de retirada, que se deduce de la fórmula iterativa (en rojo), y de la dependencia analítica (en azul).
Puedes ver que coinciden y hay un máximo en k (en la página anterior del tema).
Evidentemente, no se trata de retiradas discretas, sino necesariamente de retiradas continuas a partes iguales. Así que no hay solución para retirar de manera diferente en diferentes períodos. Así que no hay solución para retirar todo al final sin retirar antes. Esto no se deduce de las condiciones del problema, sino de las fórmulas que aplicas (k es fijo, no variable ki, i=0...T)
Total de fondos retirados
el efecto se hace tangible si la tasa de crecimiento es lo suficientemente alta
Tengo dependencias similares.
Ahora intento descomponer la expresión de la derivada en potencias de k, pero no sirve: tengo que aguantar seis órdenes de magnitud. Está claro que esto no se puede resolver analíticamente. ¿Tal vez haya otras ideas? Alguien mencionó a los diphurcs...
Tengo dependencias similares.
Ahora intento descomponer la expresión de la derivada en potencias de k, pero no sirve: tengo que aguantar seis órdenes de magnitud. Está claro que esto no se puede resolver analíticamente. ¿Tal vez haya otras ideas? Alguien mencionó a los diphurcs...
Es un poco complicado desde el punto de vista analítico. Sobre q y t. Depende de alguna manera en una forma engañosa :) Al aumentar q, al aumentar t, la fracción de eliminación óptima disminuye sistemáticamente
Tengo dependencias similares.
Ahora intento descomponer la expresión de la derivada en potencias de k, pero no sirve: tengo que aguantar seis órdenes de magnitud. Está claro que esto no se puede resolver analíticamente. ¿Tal vez haya otras ideas? Alguien mencionó a los diphurcs...
Se puede ir de lo particular a lo general. Por ejemplo, si t = 1, sólo se puede retirar dinero una vez, por lo que hay que retirar en la cantidad de q. A continuación, considere el caso para t = 2, t = 3, etc.
Es decir, si en t = 2 es óptimo retirar menos de q a la vez, entonces encuentra un extremo y generaliza para todo q en t = 2.
De forma similar para t = 3, t = 4, etc.
A partir del valor del extremo, se podrá obtener el tamaño de la retirada como f(t)
Se puede considerar que un esquema de buque conectado compone la UD.
Volumen inicial del primer recipiente B0
Se puede ir de lo particular a lo general. Por ejemplo, si t = 1, sólo se puede retirar dinero una vez y, por tanto, hay que retirarlo en la cantidad q. A continuación, considere el caso para t = 2, t = 3, etc.
A partir del valor del extremo podremos obtener el tamaño de la retirada como f(t)
Puede que tengas razón. Excepto que para t = 3 ya tenemos según la ecuación
grado k - tres en la primera derivada df(k)/dk=0, y tenemos que buscar raíces de la ecuación cúbica con todo lo que implica... Es decir, no podemos llegar más allá de t=3 en este escenario. Recordemos que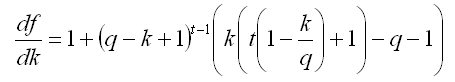 
, y para t=1 tamaño óptimo k=q, para t=2 k=q, para t=3 k=q. Pero aumentar más t y resolver analíticamente no funciona. Si se resuelve numéricamente, se puede ver que a la tasa de crecimiento del depósito q está dentro del 10% mensual y la tasa óptima de retirada es inferior a q en t>30 meses.
La conclusión es la siguiente: si la fiabilidad de la ST es tal que la vida media del depósito no supera los 3 años, entonces el comportamiento óptimo es la retirada mensual de todo el beneficio obtenido (el depósito no crece). De lo contrario, tenemos que encontrar una solución analítica para el porcentaje óptimo de retirada k y actuar según la fórmula. Este escenario garantiza el máximo de dinero de bolsillo durante el tiempo de vida previsto del depósito.
Para hacer la UD podemos considerar el esquema de vasos conectados.Volumen inicial del primer vaso B0
Si los recipientes (flujo de fluido) están en equilibrio dinámico (es decir, cuánto fluido por unidad de tiempo entra en el primer recipiente como el que sale del último) el problema sobre el nivel de agua en cada recipiente se resuelve de forma elemental y no se reduce al problema del depósito. Si considerar los vasos en proceso de su llenado no es clara la analogía con el depósito. avtomat ,explique, por favor, lo que quiso decir proponiendo tal interpretación?
P.D . El llamamiento para obtener una solución analítica aproximada de la ecuación df/dk=0 sigue siendo válido. Cualquier idea es bienvenida.