Por favor, aplique la prueba ADF y otras pruebas para comprobar la cointegración.
Otro regalo de fxsaber, gracias )
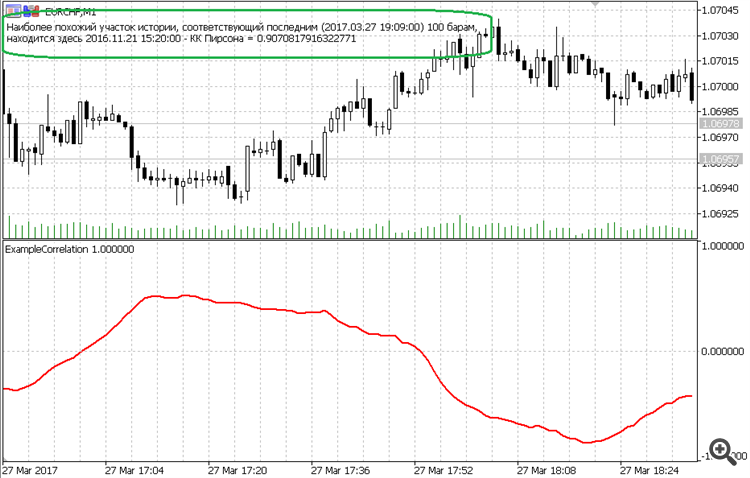
// El indicador muestra el grado de similitud de cada intervalo histórico con el intervalo actual #property indicator_separate_window #property indicator_buffers 1 #property indicator_plots 1 #property indicator_minimum -1 #property indicator_maximum 1 #property indicator_color1 clrRed #property indicator_type1 DRAW_LINE #property indicator_width1 2 sinput int Amount = 100; // Número de últimos compases (Patrón) #include <fxsaber\Math\Math.mqh> // https://www.mql5.com/es/code/17982 double Buffer[]; void OnInit() { SetIndexBuffer(0, Buffer); } int OnCalculate( const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[] ) { if (rates_total > prev_calculated) { double Pattern[]; ArrayCopy(Pattern, open, 0, rates_total - Amount, Amount); MathCorrelationPearson(open, Pattern, Buffer); const int Pos = ArrayMaximum(Buffer, 0, rates_total - Amount); Comment("El tramo de historia más similar correspondiente al más reciente (" + (string)time[rates_total - 1] + ") " + (string)Amount + "Baram, está aquí." + (string)time[Pos] + " - CI de Pearson = " + (string)Buffer[Pos]); } return(rates_total); }
Un ejemplo de cómo encontrar rápidamente la pieza más similar (según Pearson) de la historia.
La fuerza de la aplicación es sólo en el algoritmo - mucho más rápido que cualquier otro.
fxsaber:
Un ejemplo de cómo encontrar rápidamente la pieza más similar (según Pearson) de la historia.
La fuerza de la aplicación es sólo en el algoritmo - mucho más rápido que cualquier otro.
En la historia, eso es bueno. Pero me gustaría hacerlo al revés, seleccionar varios fragmentos de barra en la historia, y el indicador nos notifica al respecto si ve coincidencias. ¿Es posible en principio tal implementación?
s22aa:
En el histórico está bien. Pero me gustaría hacerlo al revés, seleccionar varios fragmentos de barras en el histórico, y que el indicador nos avise de ello si ve coincidencias. ¿Es posible en principio esa implementación?
Para ello bastaría con un simple MathCorrelationPearson estándar.
En el histórico está bien. Pero me gustaría hacerlo al revés, seleccionar varios fragmentos de barras en el histórico, y que el indicador nos avise de ello si ve coincidencias. ¿Es posible en principio esa implementación?
fxsaber:
Un simple MathCorrelationPearson interno será suficiente.
Un simple MathCorrelationPearson interno será suficiente.
Pues me parece estupendo. Acabo de empezar a estudiar C++ en cursos, ya he pasado ciclos y me siento casi un gurú de la programación, bueno, no del todo un gurú claro así que a medias, un medio gurú en una palabra. Creo que dentro de unos años el MathCorrelationPearson estándar también me resultará "sencillo".
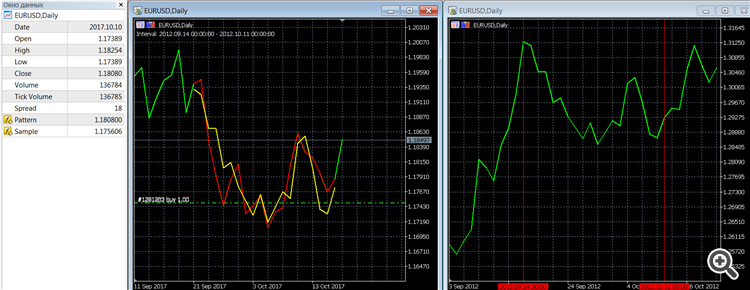
// Ejemplo de búsqueda del intervalo "más similar" al actual (criterio QC de Pearson). #property indicator_chart_window #property indicator_buffers 2 #property indicator_plots 2 #property indicator_color1 clrRed #property indicator_type1 DRAW_LINE #property indicator_width1 2 #property indicator_color2 clrYellow #property indicator_type2 DRAW_LINE #property indicator_width2 2 sinput int inAmount = 20; // Número de últimos compases (Patrón) input int inMaxBars = 1 e5; // Número de barras a analizar #include <fxsaber\Math\Math.mqh> // https://www.mql5.com/es/code/17982 double Buffer0[]; double Buffer1[]; double Buffer2[]; int handle; const long handleChart = ChartOpen(_Symbol, PERIOD_CURRENT); void OnInit() { SetIndexBuffer(0, Buffer0); SetIndexBuffer(1, Buffer1); PlotIndexSetString(0, PLOT_LABEL, "Pattern"); PlotIndexSetString(1, PLOT_LABEL, "Sample"); ChartSetInteger(handleChart, CHART_MODE, CHART_LINE); ChartSetInteger(handleChart, CHART_AUTOSCROLL, false); } //------ // Tomado de Include\Math\Stat\Math.mqh - https://www.mql5.com/ru/forum/97153/page15#comment_5927026 const double QNaN =(double)"nan"; // QNaN. //+------------------------------------------------------------------+ //| Calcula el valor medio de los valores del array[] | //+------------------------------------------------------------------+ double MathMean(const double &array[]) { int size=ArraySize(array); //--- comprueba el rango de datos if(size<1) return(QNaN); // necesita al menos 1 observación //--- calcular la media double mean=0.0; for(int i=0; i<size; i++) mean+=array[i]; mean=mean/size; //--- devolver media return(mean); } //+------------------------------------------------------------------+ //| Calcula la varianza de los valores del array[] | //+------------------------------------------------------------------+ double MathVariance(const double &array[]) { int size=ArraySize(array); //--- comprueba el rango de datos if(size<2) return(QNaN); // necesita al menos 2 observaciones //--- calcular la media double mean=0.0; for(int i=0; i<size; i++) mean+=array[i]; mean=mean/size; //--- calcular la varianza double variance=0; for(int i=0; i<size; i++) variance+=MathPow(array[i]-mean,2); variance=variance/size; //--- devolver varianza return(variance); } //------ // Adapta la muestra al patrón void NormalizeArray( const double &Pattern[], double &Sample[], const bool Reverse = false ) { const double MeanPattern = MathMean(Pattern); const double MeanSample = MathMean(Sample); const double Koef = (Reverse ? -1 : 1) * MathSqrt(MathVariance(Pattern) / MathVariance(Sample)); const int Total = ArraySize(Pattern); for (int i = 0; i < Total; i++) Sample[i] = (Sample[i] - MeanSample) * Koef + MeanPattern; } void MathLog( double &Array[] ) { for (int i = ArraySize(Array) - 1; i >= 0; i--) Array[i] = MathLog(Array[i]); } void MathExp( double &Array[] ) { for (int i = ArraySize(Array) - 1; i >= 0; i--) Array[i] = MathExp(Array[i]); } // Encuentra la mejor muestra por patrón int GetSample1( const int Amount, const double &Prices[], double &Sample[], double &Pattern[], int MaxBars ) { const int Total = ArraySize(Prices) - 1; // Eliminar la última barra de los cálculos ArrayCopy(Pattern, Prices, 0, Total - Amount, Amount); MaxBars = (Total > MaxBars) ? MaxBars : Total; double Prices2[]; ArrayCopy(Prices2, Prices, 0, Total - MaxBars, MaxBars); MathLog(Prices2); double Pattern2[]; ArrayCopy(Pattern2, Pattern); MathLog(Pattern2); double Pearson[]; MathCorrelationPearson(Prices2, Pattern2, Pearson); const int PosMax = ArrayMaximum(Pearson, 0, MaxBars - Amount); const int PosMin = ArrayMaximum(Pearson, 0, MaxBars - Amount); const bool Res = (MathAbs(Pearson[PosMax]) < MathAbs(Pearson[PosMin])); const int Pos2 = Res ? PosMin : PosMax; ArrayCopy(Sample, Prices2, 0, Pos2 - Amount + 1, Amount); NormalizeArray(Pattern2, Sample, Res); MathExp(Sample); return(Pos2 + Total - MaxBars); } void OnDeinit( const int ) { ChartClose(handleChart); } int OnCalculate( const int rates_total, const int prev_calculated, const datetime &time[], const double &open[], const double &high[], const double &low[], const double &close[], const long &tick_volume[], const long &volume[], const int &spread[] ) { if (rates_total > prev_calculated) { double Pattern[]; double Sample[]; const int Pos = GetSample1(inAmount, close, Sample, Pattern, inMaxBars); // Hemos derivado el propio patrón ArrayInitialize(Buffer0, EMPTY_VALUE); ArrayCopy(Buffer0, Pattern, rates_total - inAmount - 1); // Muestra de salida ArrayInitialize(Buffer1, EMPTY_VALUE); ArrayCopy(Buffer1, Sample, rates_total - inAmount - 1); Comment("Interval: " + (string)time[Pos - inAmount + 1] + " - " + (string)time[Pos]); // Mostrar la sección encontrada const int Offset = 10; ChartNavigate(handleChart, CHART_BEGIN, Pos - inAmount + 1 - Offset); // Desplazar el gráfico por barras Offset antes del inicio de la fuente Sample ObjectCreate(handleChart, "Left", OBJ_VLINE, 0, time[Pos - inAmount + 1], 0); ObjectCreate(handleChart, "Right", OBJ_VLINE, 0, time[Pos], 0); } return(rates_total); }
Está perdiendo oportunidades comerciales:
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Registro
Entrada
Usted acepta la política del sitio web y las condiciones de uso
Si no tiene cuenta de usuario, regístrese
Biblioteca multiplataforma de funciones matemáticas originales:
Autor: fxsaber