Tipos de matrices y vectores

Un vector es un array unidimensional de tipo real o complejo, mientras que una matriz es un array bidimensional de tipo real o complejo. Así, la lista de tipos numéricos válidos para los elementos de estos objetos incluye double (considerado el tipo por defecto), float y complex.

Desde el punto de vista del álgebra lineal (¡pero no del compilador!), un número primo es también un vector mínimo, y un vector, a su vez, puede considerarse un caso especial de matriz.

El vector, dependiendo del tipo de elementos, se describe utilizando una de las palabras clave vector (con o sin sufijo):

• vector es un vector con elementos de tipo double
• vectorf es un vector con elementos de tipo float
• vectorc es un vector con elementos de tipo complex

Aunque los vectores pueden ser verticales y horizontales, MQL5 no hace tal división. La orientación requerida del vector viene determinada (implícitamente) por la posición del vector en la expresión.

Se definen las siguientes operaciones en vectores: suma y multiplicación, así como el método Norm (con la correspondiente norma ), que obtiene el módulo o longitud del vector.

Puede pensar en una matriz como en un array, donde el primer índice es el número de fila y el segundo índice, el número de columna. No obstante, la numeración de filas y columnas, a diferencia del álgebra lineal, empieza por cero, como en los arrays.

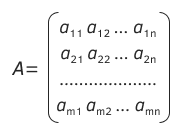
Las dos dimensiones de las matrices también se denominan ejes y se numeran del siguiente modo: 0 para el eje horizontal (a lo largo de las filas) y 1 para el eje vertical (a lo largo de las columnas). Los números de eje se utilizan en muchas funciones matriciales. En concreto, cuando hablamos de dividir una matriz en partes, dividir horizontalmente significa cortar entre filas, y dividir verticalmente significa cortar entre columnas.

Dependiendo del tipo de elementos, la matriz se describe utilizando una de las palabras clave matrix (con o sin sufijo):

• matrix es una matriz con elementos de tipo double
• matrixf es una matriz con elementos de tipo float
• matrixc es una matriz con elementos de tipo complex

Para su aplicación en funciones de plantilla, puede utilizar la notación matrix<double> , matrix<float> , matrix<complex> , vector<double> , vector<float> , vector<complex> en lugar de los tipos correspondientes.

Cuando se registran, las matrices y los vectores se imprimen como secuencias de números separados por comas y encerrados entre corchetes.

Para las matrices se definen las siguientes operaciones algebraicas:

• Suma de matrices del mismo tamaño
• Multiplicación de matrices de un tamaño adecuado, cuando el número de columnas de la primera matriz debe ser igual al número de filas de la segunda matriz.
• Multiplicación de una matriz por un vector columna y multiplicación de un vector fila por una matriz según las reglas de multiplicación de matrices (un vector es, en este sentido, un caso especial de matriz).
• Multiplicación de una matriz por un número

Además, los tipos matrix y vector tienen métodos integrados que corresponden a análogos de la biblioteca NumPy (un paquete popular para el aprendizaje automático en Python), por lo que puede obtener más pistas en la documentación y en los ejemplos de la biblioteca. Encontrará una lista completa de métodos en la correspondiente sección de ayuda de MQL5.

Por desgracia, MQL5 no permite convertir matrices y vectores de un tipo a otro (por ejemplo, de double a float). Además, el compilador no trata automáticamente a un vector como una matriz (con una columna o fila) en expresiones en las que se espera una matriz. Esto significa que el concepto de herencia (característico de la programación orientada a objetos) entre matrices y vectores no existe, a pesar de la aparente relación entre estas estructuras.