Métodos de aprendizaje automático

Entre los métodos integrados de matrices y vectores, hay varios que son demandados en tareas de aprendizaje automático, en concreto en la implementación de redes neuronales.

Como su nombre indica, una red neuronal es un conjunto de muchas neuronas, que son las células de cálculo primitivas. Son primitivas en el sentido de que realizan cálculos bastante sencillos: por regla general, una neurona tiene un conjunto de coeficientes de peso que se aplican a determinadas señales de entrada, tras lo cual la suma ponderada de las señales se introduce en la función, que es un convertidor no lineal.

El uso de una función de activación amplifica las señales débiles y limita las demasiado fuertes, evitando el paso a la saturación (desbordamiento de los cálculos reales). Sin embargo, lo más importante es que la no linealidad dota a la red de nuevas capacidades de cálculo, lo que permite resolver problemas más complicados.

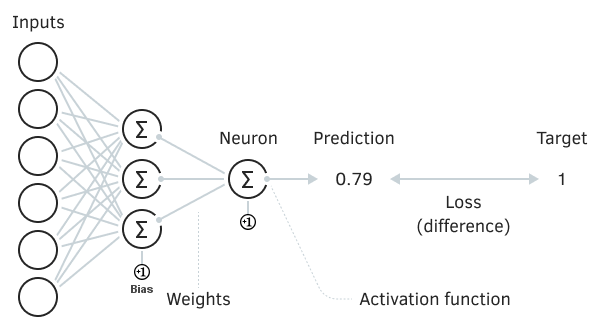
Red neuronal elemental

La potencia de las redes neuronales se manifiesta combinando un gran número de neuronas y estableciendo conexiones entre ellas. Normalmente, las neuronas se organizan en capas (que pueden compararse con matrices o vectores), incluidas aquellas que tienen conexiones recursivas (recurrentes), y también pueden tener funciones de activación que difieren en su efecto. Esto permite analizar datos volumétricos mediante diversos algoritmos, en concreto mediante la búsqueda de patrones ocultos en ellos.

Obsérvese que, si no fuera por la no linealidad de cada neurona, una red neuronal multicapa podría representarse de forma equivalente como una sola capa, cuyos coeficientes se obtienen por el producto matricial de todas las capas (Wtotal = W1 * W2 * ... * WI-D, donde 1..L es el número de capas). Y esto sería un simple sumador lineal. Por tanto, se corrobora matemáticamente la importancia de las funciones de activación.

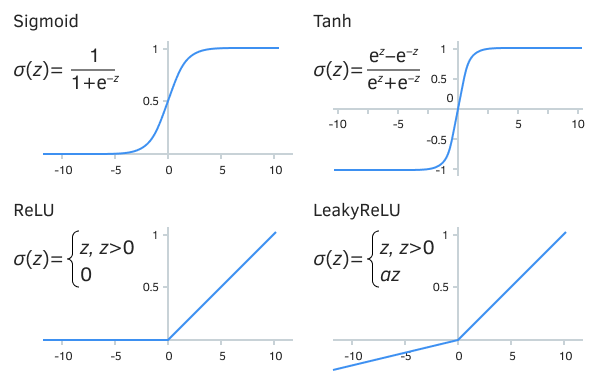
Algunas de las funciones de activación más famosas

Una de las principales clasificaciones de las redes neuronales las divide según el algoritmo de aprendizaje utilizado en redes de aprendizaje supervisado y no supervisado. Las supervisadas requieren que un experto humano proporcione los resultados deseados para el conjunto de datos original (por ejemplo, marcadores discretos del estado de un sistema de trading, o indicadores numéricos de incrementos de precios implícitos). Las redes no supervisadas identifican por sí solas conjuntos en los datos.

En cualquier caso, la tarea de entrenar una red neuronal consiste en buscar parámetros que minimicen el error en las muestras de entrenamiento y de prueba, para lo cual se utiliza la función de pérdida: ésta proporciona una estimación cualitativa o cuantitativa del error entre el objetivo y la respuesta recibida de la red.

Los aspectos más importantes de la correcta aplicación de las redes neuronales incluyen la selección de predictores informativos e independientes entre sí (características analizadas), la transformación de los datos (normalización y limpieza) según las especificidades del algoritmo de aprendizaje, y la optimización de la arquitectura y el tamaño de la red. Tenga en cuenta que el uso de algoritmos de aprendizaje automático no garantiza el éxito.

Aquí no entraremos en la teoría de las redes neuronales, su clasificación y las tareas típicas que deben resolver, ya que se trata de un tema demasiado amplio. Los interesados pueden encontrar artículos en la web mql5.com y en otras fuentes.

MQL5 proporciona tres métodos de aprendizaje automático que han pasado a formar parte de la API de matrices y vectores.

• Activation calcula los valores de la función de activación.
• Derivative calcula los valores de la derivada de la función de activación.
• Loss calcula el valor de la función de pérdida.

Las derivadas de las funciones de activación permiten actualizar eficazmente los parámetros del modelo en función del error que cambia durante el proceso de aprendizaje.

Los dos primeros métodos escriben el resultado en el vector/matriz pasado y devuelven un indicador de éxito (true o false), y la función de pérdida devuelve un número. Veamos sus prototipos (bajo el tipo object<T> hemos marcado ambos, matrix<T> y vector<T>):

bool object<T>::Activation(object<T> &out, ENUM_ACTIVATION_FUNCTION activation)

bool object<T>::Derivative(object<T> &out, ENUM_ACTIVATION_FUNCTION loss)

T object<T>::Loss(const object<T> &target, ENUM_LOSS_FUNCTION loss)

Algunas funciones de activación permiten establecer un parámetro con un tercer argumento opcional.

Consulte la documentación de MQL5 para ver la lista de funciones de activación admitidas en la enumeración ENUM_ACTIVATION_FUNCTION y las funciones de pérdida en la enumeración ENUM_LOSS_FUNCTION.

Como ejemplo introductorio, consideremos el problema de analizar el flujo de ticks reales. Algunos operadores consideran que los ticks son ruido basura, mientras que otros practican trading de alta frecuencia basado en ticks. Existe la presunción de que los algoritmos de alta frecuencia, por regla general, dan ventaja a los grandes operadores y se basan únicamente en el tratamiento informático de la información sobre precios. Basándonos en esto, plantearemos la hipótesis de que existe un efecto de memoria a corto plazo en el flujo de ticks, debido a los actuales robots activos de los creadores de mercado. A continuación, se puede utilizar un método de aprendizaje automático para encontrar esta dependencia y predecir varios ticks futuros.

El aprendizaje automático siempre implica plantear hipótesis, sintetizar un modelo para las mismas y probarlas en la práctica. Obviamente, no siempre se obtienen hipótesis productivas. Se trata de un largo proceso de ensayo y error, en el que el fracaso es fuente de mejoras y nuevas ideas.

Utilizaremos uno de los tipos más sencillos de redes neuronales: la Memoria Asociativa Bidireccional (BAM, por sus siglas en inglés). Una red de este tipo sólo tiene dos capas: entrada y salida. Se forma una determinada respuesta (asociación) en la salida en respuesta a la señal de entrada. El tamaño de las capas puede variar. Cuando los tamaños son iguales, el resultado es una red de Hopfield.

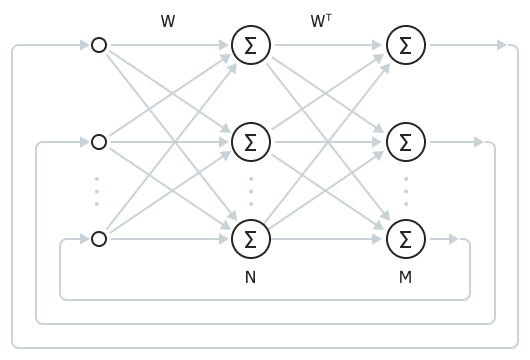
Memoria asociativa bidireccional totalmente conectada

Utilizando una red de este tipo, compararemos N ticks previos recientes y M ticks próximos previstos, formando una muestra de entrenamiento desde el pasado cercano hasta una profundidad determinada. Los ticks se introducirán en la red como incrementos de precio positivos o negativos convertidos a valores binarios [+1, -1] (las señales binarias son la forma canónica de codificación en las redes BAM y Hopfield).

La ventaja más importante de BAM es el proceso de aprendizaje casi instantáneo (en comparación con la mayoría de los demás métodos iterativos), que consiste en calcular la matriz de pesos. Mas abajo le ofrecemos la fórmula.

Sin embargo, esta simplicidad también tiene un inconveniente: la capacidad de BAM (el número de imágenes que puede recordar) está limitada al tamaño de capa más pequeño, siempre que se cumpla la condición de una distribución especial de +1 y -1 en los vectores de la muestra de entrenamiento.

Así, para nuestro caso, la red generalizará todas las secuencias de ticks de la muestra de entrenamiento y luego, en el curso de un trabajo regular, pasará a una u otra imagen almacenada, en función de la secuencia de nuevos ticks presentada. El resultado en la práctica depende de un gran número de factores, como el tamaño y la configuración de la red, las características del flujo de ticks actual, etc.

Como se supone que el flujo de ticks sólo tiene memoria a corto plazo, es conveniente volver a entrenar la red en tiempo real o casi, ya que el entrenamiento se reduce en realidad a varias operaciones matriciales.

Así, para que la red recuerde las imágenes asociativas (en nuestro caso, el pasado y el futuro del flujo de ticks), se requiere la siguiente ecuación:

donde W es la matriz de pesos de la red. La suma se realiza sobre todos los productos por pares de los vectores de entrada Ai y los correspondientes vectores de salida Bi.

A continuación, cuando la red está en funcionamiento, suministramos la imagen de entrada a la primera capa, le aplicamos la matriz W y activamos así la segunda capa, en la que se calcula la función de activación de cada neurona. Seguidamente, utilizando la matriz W T transpuesta, la señal se propaga de nuevo a la primera capa, donde también se aplican funciones de activación en las neuronas. En este momento, la imagen de entrada ya no llega a la primera capa, es decir, el proceso oscilatorio libre continúa en la red. Continúa hasta que los cambios en la señal de las neuronas de la red se estabilizan (es decir, se vuelven inferiores a un determinado valor predeterminado).

En este estado, la segunda capa de la red contiene la imagen de salida asociada encontrada: la predicción.

Vamos a implementar este escenario de aprendizaje automático en el script MatrixMachineLearning.mq5.

En los parámetros de entrada, puede establecer el número total de últimos ticks (TicksToLoad) solicitados al historial, y cuántos de ellos se asignan a las pruebas (TicksToTest). En consecuencia, el modelo (ponderaciones) se basará en ticks (TicksToLoad - TicksToTest).

Además, en las variables de entrada, se seleccionan los tamaños del vector de entrada (el número de ticks conocidos PredictorSize) y del vector de salida (el número de ticks futuros ForecastSize).

Los ticks se solicitan al principio de la función OnStart. En este caso, sólo trabajamos con los precios de Ask. No obstante, también puede añadir el proceso Bid y Last, junto con los volúmenes.

Dividamos los ticks en conjuntos de entrenamiento y de prueba.

Para calcular los incrementos de precio utilizamos el método Convolve con un vector adicional {+1, -1}. Tenga en cuenta que el vector con incrementos será 1 elemento más corto que el original.

La convolución según el algoritmo VECTOR_CONVOLVE_VALID significa que sólo se tienen en cuenta los solapamientos completos de los vectores (es decir, el vector más pequeño se desplaza de forma secuencial a lo largo del más grande sin salirse de sus límites). Otros tipos de convoluciones permiten que los vectores se solapen sólo con un elemento, o con la mitad de los elementos (en este caso, los elementos restantes están más allá del vector correspondiente y los valores de la convolución muestran efectos de borde).

Para convertir los valores continuos de los incrementos en impulsos unitarios (positivos y negativos dependiendo del signo del elemento inicial del vector), utilizaremos una función auxiliar Binary (no mostrada aquí): devuelve una nueva copia del vector en la que cada elemento es +1 o -1.

Basándonos en la secuencia de entrada recibida, utilizamos la función TrainWeights para calcular la matriz de pesos de la red neuronal W. Más adelante estudiaremos la estructura de esta función. Por ahora, preste atención a que se le pasan los parámetros PredictorSize y ForecastSize, lo que permite dividir una secuencia continua de ticks en conjuntos de vectores de entrada y salida emparejados según el tamaño de las capas BAM de entrada y salida, respectivamente.

Inmediatamente después de entrenar la red, comprobamos su precisión en el conjunto de entrenamiento, sólo para asegurarnos de que la red ha sido entrenada. Para ello se utiliza la función CheckWeights.

No obstante, es más importante comprobar cómo se comporta la red con datos de prueba desconocidos. Para ello, vamos a diferenciar y «binarizar» el segundo vector ask2, y después a enviarlo también a CheckWeights.

Es hora de familiarizarse con la función TrainWeights, en la que definimos las matrices A y B para «cortar» vectores de la secuencia de entrada pasada, es decir, del vector data.

Cada patrón A sucesivo se obtiene a partir de ticks consecutivos en cantidad igual a predictor, y el patrón futuro correspondiente se obtiene a partir de los siguientes elementos response. Mientras la cantidad total de datos lo permita, esta ventana se desplaza hacia la derecha, un elemento cada vez, formando más pares nuevos de imágenes. Las imágenes se numeran por filas y los ticks que aparecen en ellas se numeran por columnas.

A continuación, debemos asignar memoria a la matriz de pesos W y llenarla utilizando métodos matriciales: multiplicamos secuencialmente las filas de A y B utilizando Outer, y luego realizamos la suma matricial.

La función CheckWeights realiza acciones similares para una red neuronal, cuyos coeficientes de peso se pasan ya preparados en el primer argumento W. Los tamaños de los vectores de entrenamiento se extraen de la propia matriz W.

En este caso, las matrices A y B no se forman para calcular W, sino que actúan como «proveedoras» de vectores para las pruebas. También necesitamos una copia transpuesta de W para calcular las señales de retorno de la segunda capa de red a la primera.

El número de iteraciones durante las cuales se permiten procesos transitorios en la red, hasta la convergencia, está limitado por la constante limit.

Las variables positive, negative, y average son necesarias para calcular las estadísticas de predicciones acertadas y fallidas a fin de evaluar la calidad del entrenamiento.

Además, la red se activa en un bucle sobre pares de patrones de prueba y se toma su respuesta final. Cada vector de entrada siguiente se escribe en el vector ay la capa de salida b se rellena con ceros. A continuación, se lanzan iteraciones para la transmisión de la señal de a a b utilizando la matriz W y aplicando la función de activación AF_TANH, así como para la señal de realimentación de b a a, y también el uso de AF_TANH. El proceso continúa hasta alcanzar limit bucles (lo cual es improbable) o hasta que se cumpla la condición de convergencia, bajo la cual los vectores a y b de estado de las neuronas prácticamente no cambian (aquí utilizamos el método Compare y copias auxiliares de x e y de la iteración anterior).

Tras alcanzar un estado estable, transferimos los estados de las neuronas de continuo (real) a binario +1 y -1 utilizando la función Binarize (es similar a la función Binary mencionada anteriormente, pero cambia el estado del vector en su lugar).

Ahora, sólo tenemos que contar el número de coincidencias en la capa de salida con el vector objetivo. Para ello, realice una multiplicación escalar de vectores. Un resultado positivo significa que el número de aciertos supera al de errores. El recuento total de aciertos se acumula en «media».

Una vez completado el ciclo para todas las muestras de prueba, se muestran las estadísticas.

El script también incluye la función RunWeights, que representa una ejecución de trabajo de la red neuronal (por su matriz de pesos W) para el vector en línea de los últimos ticks predictor. La función devolverá un vector con los ticks futuros estimados.

Al final de OnStart, pausamos la ejecución durante 1 segundo (para esperar nuevos ticks con un cierto grado de probabilidad), solicitamos los últimos ticks PredictorSize + 1 (no olvidemos +1 para la diferenciación), y hacemos predicciones para ellos en línea.

Al ejecutar el script con la configuración predeterminada en EURUSD el viernes por la tarde, se obtuvieron los siguientes resultados:

El símbolo y la hora no se mencionan, ya que la situación del mercado puede afectar significativamente a la aplicabilidad del algoritmo y a la configuración específica de la red. Cuando el mercado esté abierto, cada vez que ejecute el script obtendrá nuevos resultados a medida que entren más y más ticks. Este es un comportamiento esperado coherente con la hipótesis de formación de memoria a corto plazo.

Como podemos ver, la precisión de entrenamiento es aceptable, pero disminuye notablemente en los datos de prueba y puede caer por debajo del 50 %.

En este punto, pasamos sin problemas de la programación al campo de la investigación científica. El conjunto de herramientas de aprendizaje automático integrado en MQL5 le permite implementar muchas otras configuraciones de analizadores y redes neuronales, con diferentes estrategias de trading y principios de preparación de los datos iniciales.