Denis, I have this comment on the article.
As for theory, there are no questions, everything is presented in detail.
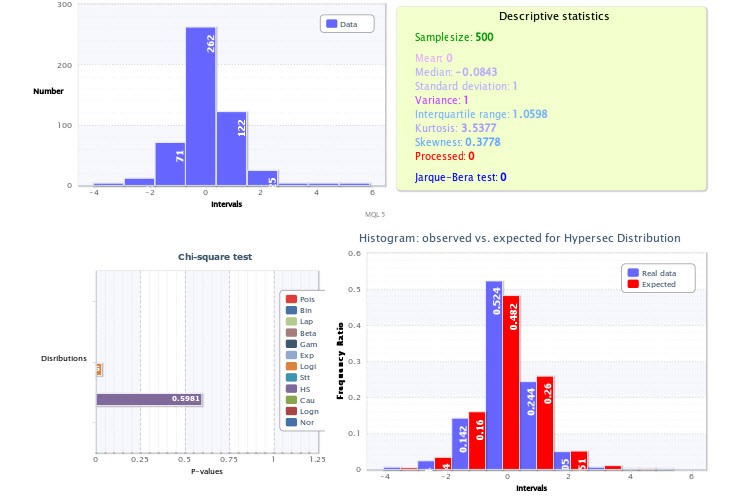
As for practice, I would like to draw your attention to the figures where you show empirical histograms, especially Figure 2. The point is that you made two very significant inaccuracies in your analysis.
Firstly, you have set too small number of classes for the script generating the histograms - only 9, which in itself is a huge blow to the power of Pearson's criterion and makes its application ineffective. For the future, take 200-300 classes to be sure, of course, if the sample size allows (and it does), you won't make a mistake. If you had done exactly that, you would have been able to make sure that the test for lognormal distribution would have given a negative result, as well as the test of returns for hypersecans. By the way, it is very easy to make sure that two such distributions cannot simultaneously represent a certain value and its modulus, just take the "half" of the hypersecance and convolve it with itself (analogue to taking the modulus from a random variable): you will definitely not get a lognormal one.
The second inaccuracy is that you did not use the a priori knowledge that the top (aka expectation) of the distribution of returns must be exactly at 0 (otherwise we would all have been billionaires long ago). That is why the histogram in Figure 2 looks shifted to the right, although it should not. Again, taking this into account when plotting the histogram would make the tests more reliable.
P.S. I am writing an article on the basics of modelling, hence such a keen interest. Thank you for your article, it is in the topic. Regards.
...Firstly, you have set too small number of classes for the script generating histograms - only 9, which in itself is a big blow to the power of Pearson's criterion and makes its application ineffective. For the future, take 200-300 classes to be sure, of course, if the sample size allows (and it does), you won't make a mistake. If you had done it this way, you would be able to make sure that the test for lognormal distribution would give a negative result, as well as the test of returns for hypersecans. By the way, it is very easy to make sure that two such distributions cannot represent a certain value and its modulus at the same time, just take the "half" of the hypersecance and convolve it with itself (analogue of taking the modulus from a random value): you will definitely not get a lognormal one.
Dear alsu, thanks for your opinion!
Let's go in order.
The number of classes is not set voluntarily, but according to some formula. In my case it is Sturgis formula. It's one of the most popular rules. It's not perfect, I agree with that. But still...
And you take 200-300 classes according to what rule?
The second inaccuracy is that you did not use the a priori knowledge that the top (aka expectation) of the distribution of returns must be exactly at 0 (otherwise we would all have been billionaires long ago). That is why the histogram in Figure 2 looks shifted to the right, although it should not. Again, taking this point into account when constructing the histogram would make the tests more reliable.
I analyse the sample on a factual basis. I analyse what I have. And on what basis should the top of the yield distribution be exactly at the point 0? Maybe I'm misunderstanding something...
And besides, if you look at the distribution to which the fitting was implemented (which was X~HS(-0.00, 1.00)), it is easy to see that the first parameter - the shift parameter - is exactly 0. In fact, it is equal to the expectation.
Here is another html report on sampling the standard values. I hope the figure is more or less readable. But it is not identical to the one in the article. I just took the latest data just now.
As you can see, Mean =0. And the best fit is the Hyperbolic Secant distribution: X~HS(0.00, 1.00).
Exactly, Sturges' formula gave exactly 9 classes, but this is rather a reason to think about increasing the sample size (reversing the formula, I see that you have it around 256?).
Besides, this formula works well only for general populations from normal distribution (for which it was derived) and, as it is considered, the sample size is not more than 200 values. You can use alternative formulas - Diakonis, Scott....
In general, you know, Sturges never gave a logical justification of his formula - yes, it is based on approximation of normal distribution by binomial distribution, so what? How can this affect the question of the efficiency of choosing the number of classes? The optimality criterion was never defined by the author and the formula itself was written at random. But the point is that for a long time Sturges' approach was the only one that was formalised in any way, and it was automatically (and, in my opinion, quite thoughtlessly!) included in all statistical packages, which, by the way, is quite annoying precisely because this formula almost always gives an extremely underestimated number of classes.
Once again, there are alternative formulas, but it is the presence of a personal computer, paradoxically enough, gives us the opportunity to use our own head as a device, i.e. a visual way of determining a more or less optimal number of classes for this particular sample, when, smoothly changing this indicator, we achieve a compromise between the smoothness of the graph and the resolution of the histogram. By the way, this method is often better and faster than any formulae.
I always say to everyone - before putting numbers into formulas, ask what it means and how (and whether) to apply it. In short, I am against using Sturges' formula, I consider it outdated and inadequate).
Regarding the mean. The expectation of returns should be at 0 because if it were not so, we could stupidly bet always in one direction, corresponding to the sign of this MO, and be guaranteed to get a return of any pre-determined size. Well, the top should coincide with the MO purely for reasons of symmetry: the left half of the graph should be a mirror image of the right one (the rate increase and decrease are statistically equal, and there should be no differences between them), so the centre of symmetry coincides with the centre.
Since you take HS(0.00, 1.00), therefore, you should centre the classes - i.e. the zero class should include the index values in some symmetric interval (-x0;x0), otherwise we introduce into the calculations a systematic error associated with the shift of classes relative to zero, and it eventually creeps into the result of the chi^2 test. Your point 0 is not in the middle of the zero class.
In fact, the question of how to make classes symmetric on discrete data is quite nontrivial, and, again, it is good to solve it for each particular sample individually and very carefully, otherwise we risk getting inadequate results also because of the wrong choice of the boundaries of the division into classes.
alsu, you have touched on a topic that, although not the subject of my article, is extremely interesting. As much as I can, I will research this issue further.
Thank you for your constructive criticism!
I like your opinion about the applicability of scientific knowledge in trading.
Could you please tell me which of the books you would recommend to a person who is familiar with probability theory and mathematical statistics?
Denis, good afternoon.
I like your opinion about the applicability of scientific knowledge in trading.
Please tell me which of the books you would recommend to a person who is familiar with probability theory and mathematical statistics.
Thank you for your opinion!
I think that one should look for something for beginners then, some lit-role. The main thing is that the text of the book should not discourage you from reading it further :-))).
I liked something Gaidyshev, and something Bulashev.....
- rsdn.org
The second inaccuracy is that you have not used the a priori knowledge that the top (aka expectation) of the distribution of returns must be exactly at 0 (otherwise we would all have been billionaires long ago).
Not at all. A shift of the top of the distribution relative to 0 (growth/decline of an instrument) does not mean that it will be the same in the future. That is why most traders are not billionaires, not because.
Regards.
...Shifting the top of the distribution relative to 0 (rising/falling instrument) does not necessarily mean that this will be the case in the future...
Agreed.
Question for alsu. Did you mean market efficiency when talking about the zero point?
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
New article The Role of Statistical Distributions in Trader's Work is published:
Author: Dennis Kirichenko