Discussing the article: "Functions for activating neurons during training: The key to fast convergence?"
This passage in the article caught my eye. Even though the article is very well written and gives details of how it was designed and thought through. In this passage there is a subtlety about your understanding of the subject. Perhaps you're biased because everyone insists on saying certain things about neural networks. But your article is well written and you've explained the details involved. I've decided to anticipate something that I'll be showing in the future. The article for this has already been written, but first I want to finish explaining how to build the Replay / Simulator, where there are only a few articles left to finalise the publication. Understand the following: Activation functions are NOT used to generate non-linearity in equations. Rather, they serve as a type of filter with the aim of reducing the number of layers or perceptrons within the network being built. This speeds up the process of converging the data in a specific direction. During this process we can aim to classify or retain knowledge. In the end, we'll get one result or the other, but never both.
In my article, https://www.mql5.com/en/articles/13745, I demonstrate this in a relatively simple way. Although there, I'm just beginning to explain how to understand the neural network. But since your article is well written and you've put a lot of effort into it, I'll give you a tip. Take some apparently random data and remove the perceptron activation functions. After that, start trying to converge. You'll notice that it won't look very good. BUT if you start adding layers and/or more perceptrons, the convergence will start to improve over time. This will help you better understand why activation functions are necessary. 😁👍

- www.mql5.com
This passage from the article caught my attention. Although the article is very well written and details how it was designed and thought out. There is a subtlety in your understanding of the subject in this passage. Perhaps you are biased because everyone insists on saying certain things about neural networks. But your article is well written and you explained the details. I decided to anticipate what I will be showing in the future. The article for that is already written, but first I want to finish explaining how to build a Replay / Simulator, where there are only a few articles left to complete the publication. Understand the following: Activation functions are NOT used to create non-linearity in equations. Rather, they serve as a kind of filter whose purpose is to reduce the number of layers or perceptrons in the network being built. This speeds up the process of convergence of the data in a particular direction. During this process, we can aim for classification or knowledge retention. We will end up with one or the other result, but never both.
The auto-translation is probably not very accurate, but the highlighted is incorrect. It is nonlinearity that increases the computational power of the network, and it not only speeds up the convergence process (which you yourself also said in another sentence) but fundamentally allows you to solve problems that cannot be solved without introducing nonlinearity (no matter how many layers you add). Moreover, without nonlinearity, any (synchronous) neural network can be "collapsed" into an equivalent single-layer network.
It is nonlinearity that increases the computational power of the network, and it not only speeds up the convergence process (which you yourself also said in another sentence) but fundamentally allows you to solve problems that cannot be solved without the introduction of nonlinearity (no matter how many layers you add). Moreover, without nonlinearity, any (synchronous) neural network can be "collapsed" into an equivalent single-layer network.
+100500
Well said. While I was composing my reply, I see that it has already been answered.
I will say more, yes, any nonlinear function can be described by linear piecewise functions in number tending to infinity with description error tending to zero. But why, if nonlinear activation functions are just used to simplify the description of the object in the problem.
I think there was a misunderstanding between what I intended to say and what I actually put in text form.
I'll try to be a bit clearer this time. 🙂 When we want to CLASSIFY things, such as images, objects, figures, sounds, in short, where probabilities will reign. We need to limit the values within the neural network so that they fall within a given range. This range is usually between -1 and 1. But it can also be between 0 and 1 depending on how fast, what the hit rate is, and what kind of treatment is given to the input information that we want the network to come into contact with, and how it best directs its own learning in order to create the classification of things. IN THIS CASE, WE DO NEED activation functions. Precisely to keep the values within that range. In the end, we'll have the means to generate values in terms of the probability of the input being one thing or another. This is a fact and I don't deny it. So much so that we often need to normalise or standardise the input data.
However, neural networks are not only used for classifying things, they can and are also used for retaining knowledge. In this case, activation functions should be discarded in many cases. Detail: There are cases where we need to limit things. But these are very specific cases. This is because these functions get in the way of the network fulfilling its purpose. Which is precisely to retain knowledge. And in fact I agree, in part, with Stanislav Korotky 's comment that the network, in these cases, can be collapsed into something equivalent to a single layer, if we don't use activation functions. But when this happens, it would be one of several cases, since there are cases in which a single polynomial with several variables is not enough to represent, or rather retain, knowledge. In this case we would need to use extra layers so that the result can really be replicated. Or new ones can be generated. It's a bit confusing to explain it like this, without a proper demonstration. But it works.
The big problem is that because of the fashion for everything now, in the last 10 years or so, if memory serves, it's been linked to artificial intelligence and neural networks. Although the business has only really taken off in the last five years. Many people are completely unaware of what they really are. Or how they actually work. This is because everyone I see is always using ready-made frameworks. And this doesn't help at all to understand how neural networks work. They're just a multi-variable equation. They've been studied for decades in academic circles. And even when they came out of academia, they were never announced with such fanfare. During the initial phase and for a long time ACTIVATION FUNCTIONS WERE NOT USED. But the purpose of the networks, which at the time weren't even called neural networks, was different. However, because three people wanted to profit from them, they were publicised in a way that was somewhat wrong, in my opinion. The right thing, at least in my view, would be for them to be properly explained. Precisely so as not to create so much confusion in the minds of so many people. But that's fine, the three of them are making a lot of money while the people are more lost than a dog that's fallen off a removal lorry. In any case, I don't want to discourage you from writing new articles, Andrey Dik, but I do want you to continue studying and try to delve even deeper into this subject. I saw that you tried to use pure MQL5 to create the system. Which is very good by the way. And this caught my attention, making me realise that your article was very well written and planned. I just wanted to draw your attention to that particular point and make you think about it a little more. In fact, this subject is very interesting and there's a lot that few people know. But you went ahead and studied it.
Debates em alto nível, são sempre interessantes, pois nos faz crescer e pensar fora da caixa. Brigas não nos leva a nada, e só nos faz perder tempo. 👍

- 2025.01.21
- MetaQuotes
- www.mql5.com
Anything can be used as activation function, even cosine, the result is at the level of popular ones. It is recommended to use relu (with bias 0.1( it isnotrecommended to use ittogether with random walk initialisation)) because it is simple (fast counting) and better learning: These blocks are easy to optimise because they are very similar to linear blocks.The only differenceis that a linear rectification block outputs 0 in half of its domain ofdefinition. Therefore, the derivative of a linear rectification block remains large everywhere the block is active. Not only are the gradients large, but they are also consistent. The second derivative of the rectification operation is zero everywhere, and the firstderivative is 1 everywhere the block is active. This means that the direction of the gradient is much more useful for learning than when the activation function is subject to second-order effects... When initialising the affine transformation parameters, it is recommended toassign a small positive value toall elements of b, e.g. 0.1. Then the linear rectification block is very likely to be active at the initial moment for most training examples, and the derivative will be different from zero.
Unlike piecewise linearblocks , sigmoidalblocks are close to the asymptote in most of their domain of definition - approaching a high value when z tends to infinity and a low value when z tends to minus infinity.They have high sensitivityonly in the vicinity of zero. Due to the saturation of sigmoidal blocks, gradient learning is severely hampered. Therefore, using them as hidden blocks in forward propagation networks is nowadays not recommended ... If it is necessary to use sigmoidal activation function, it is better to take hyperbolic tangent instead of logistic sigmoid . It is closer to the identityfunction in the sense that tanh(0) = 0, whereas σ(0) = 1/2. Since tanh resembles an identity function in the neighbourhood of zero, training a deep neuralnetwork resembles training a linear model, provided that the network activation signals can be kept low.In this case, the training of a network with the activation function tanh is simplified.
For lstm we need to use sigmoid or arctangent(it is recommended to set the offsetto 1 for the forgetting vent): Sigmoidal activation functions are still used, but not in feedforward networks . Recurrent networks, many probabilistic models, and some autoencoders have additional requirements that preclude the use of piecewise linear activation functions and make sigmoidal blocks more appropriate despite saturation issues.
Linear activation and parameter reduction: If each layer of the network consists of only linear transformations, the network as a whole will be linear. However, some layers may also be purely linear - this is fine. Consider a layer of a neural network that has n inputs and p outputs. It can be replaced by two layers, one with a weight matrix U and the other with a weight matrix V. If the first layer has no activation function, we have essentially decomposed the weight matrix of the original layer based on Winto multipliers . If U generates q outputs, then U and V together contain only (n + p)q parameters, whereas W contains np parameters. For small q, the parameter savings can besubstantial. The payoff is a limitation - the linear transformation must have a low rank, but such low rank links are often sufficient. Thus, linear hidden blocks offer an efficient way to reduce the number ofnetwork parameters.
Relu is better for deep networks: Despite the popularity of rectification in early models, it was almost universally replaced by sigmoid in the 1980s because it works better for very small neural networks.
But it is better in general: for small datasets ,using rectifying nonlinearities is even more important than learning hidden layerweights .Random weights are sufficient to propagate usefulinformation through the network with linear rectification, allowing the classifyingoutput layer to be trained to map different feature vectorsto classidentifiers. If more data is available, the learning process begins to extract so much useful knowledge that it outperforms the randomly selectedparameters... learning is much easier in rectified linear networks than in deep networks for which theactivation functions are characterised by curvature or two-way saturation...
I think there was a misunderstanding between what I wanted to say and what I actually laid out in text form.
I'll try to be a little clearer this time. 🙂 When we want to TO CATEGORISE things like images, objects, shapes, sounds, in short, where probabilities will reign. We need to constrain the values in the neural network so that they fall within a given range. Usually this range is between -1 and 1. But it can also be between 0 and 1, depending on how quickly, at what rate and in what way the input information we want the network to learn is processed and how it best directs its learning to create a classification of things. IN THIS CASE, WE WILL NEED activation functions. It is to keep the values within that range. We will end up with a means of generating values in terms of the probability that the inputs are one or the other. This is a fact, and I don't deny it. So much so that we often have to normalise or standardise input data.
However, neural networks are not only used for classification, they can and are also used for knowledge retention. In this case, activation functions should be discarded in many cases. Detail: There are cases where we need to restrict something. But these are very specific cases. The point is that these functions prevent the network from fulfilling its purpose. And that is to preserve knowledge. And in fact, I partially agree with Stanislav Korotsky 's comment that the network in such cases can be reduced to something equivalent to a single layer if you don't use activation functions. But when this happens, it will be one of several cases, because there are cases where a single polynomial with several variables is not enough to represent or, better to say, store knowledge. In this case, we will have to use additional layers so that the result can actually be reproduced. Alternatively, new ones can be generated. It's a bit confusing to explain it like this, without a proper demonstration. But it works.
The big problem is that because of the fashion for everything now, in the last 10 years or so, if my memory serves me correctly, it's been about artificial intelligence and neural networks. Although the business has only really blossomed in the last five years. A lot of people are completely unaware of what these things really are. And how they actually work. This is because everyone I see is always using off-the-shelf frameworks. And that doesn't help at all to understand how neural networks work. It's just an equation with a few variables. They've been studied in academia for decades. And even when they have moved beyond academia, they have never been announced with such pomp. Initially, and for a long time. ACTIVATION FUNCTIONS WERE NOT USED. But the purpose of the networks, which were not even called neural networks at the time, was different. However, because three people wanted to capitalise on them, they were hyped, which I think is somewhat wrong. The right thing to do, at least from my point of view, would have been to properly explain their essence. Exactly so as not to create confusion in the minds of many people. But that's okay, the three of them make a lot of money and people are more lost than a dog falling off a rubbish truck. Anyway, I don't want to discourage you from writing more articles, Andrew Dick, but I want you to keep learning and try to delve even deeper into this topic. I saw that you tried to use pure MQL5 to create a system. Which is very good, by the way. It caught my attention and I realised that your article is very well written and planned. I just wanted to draw your attention to this point and make you think about it a bit more. This topic is actually very interesting and not many people know about it. But you have taken it up and researched it.
Yes, non-linearity is an indirect effect that activation phs have. They were originally intended to translate from one domain of target definition to another, for example, for classification tasks. "Nonlinearity" can be achieved in different ways, for example by increasing the number of features or transforming them, or by kernels that transform features.
The simplest example is logistic regression, which remains linear despite the activation function at the end.
But in multilayer networks, nonlinearity is obtained due to the number of layers with activation functions, simply as a consequence of kernel-type transformations.Historical Background:
You are correct that the concepts underlying logistic regression and early neural networks came before modern deep neural networks.
Let's look at the chronology:
-
Thelogistic function was developed in the 19th century. Its use as a statistical model for classification (logistic regression) became popular in the mid-20th century (roughly 1940s-50s).
-
The first mathematical model of a neuron (the McCulloch and Pitts model) with an activation function appeared in 1943. It used a simple threshold function.
-
The perceptron, a single-layer neural network, was developed by Frank Rosenblatt in 1958. It used a threshold activation function and could only solve linearly separable problems.
-
Thebreakthrough in deep learning and multilayer networks came only with the advent of the backpropagation algorithm, which was popularised in 1986 by Rumelhart, Hinton and Williams.
It was this algorithm that made it practical to train multilayer neural networks and showed that it requires not just threshold but differentiable nonlinear activation functions (such as sigmoid and later ReLU).
Conclusion:
Historically it turns out that:
-
First there were models (logistic regression, perceptron) that were essentially one-layer models.
-
In these models, the activation function really acted as a transformation to the desired domain (from a linear sum to a binary class or probability), since the entire model remained linear.
-
Later, with the advent of multilayer networks, a new, fundamentally more important role of the activation function emerged - to introduce nonlinearity into the hidden layers so that the network could learn.
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Check out the new article: Functions for activating neurons during training: The key to fast convergence?.
Imagine a river with many tributaries. In its normal state, water flows freely, creating a complex pattern of currents and whirlpools. But what happens if we start building a system of locks and dams? We will be able to control the flow of water, direct it in the right direction and regulate the strength of the current. The activation function in neural networks plays a similar role: it decides which signals to pass through and which to delay or attenuate. Without it, a neural network would be just a set of linear transformations.
The activation function adds dynamics to the neural network operation, allowing it to capture subtle nuances in the data. For example, in a face recognition task, an activation function helps the network notice tiny details, such as the arch of an eyebrow or the shape of a chin. The correct choice of activation function affects how a neural network performs on various tasks. Some features are better suited for the early stages of training, providing clear and understandable signals. Other features allow the network to pick up more subtle patterns at advanced stages, while others sort out the unnecessary ones, leaving only the most important.
If we do not know the properties of activation functions, we may run into problems. A neural network may begin to "stumble" on simple tasks or "overlook" important details. The main purpose of activation functions is to introduce nonlinearity into the neural network and normalize the output values.
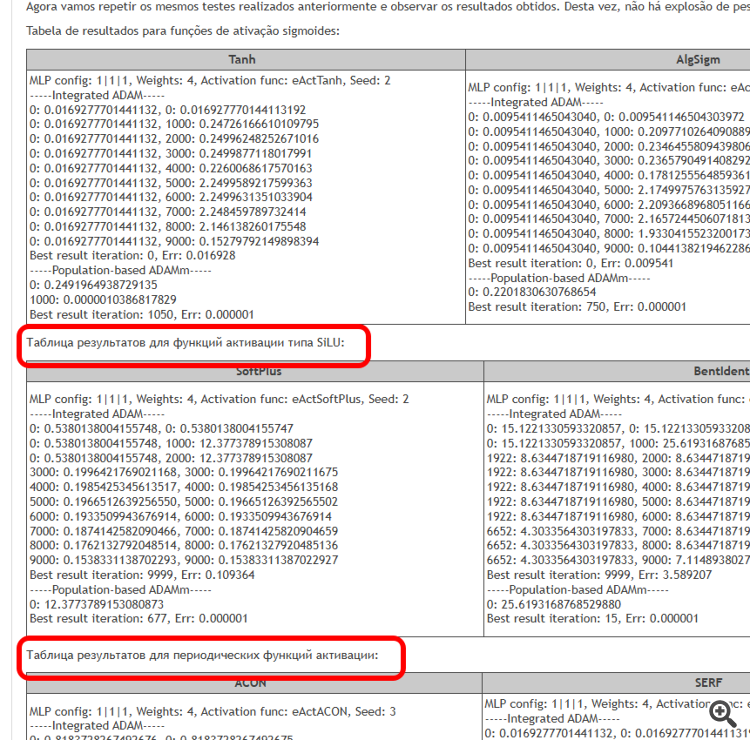
The aim of this article is to identify the issues associated with the use of different activation functions and their impact on the accuracy of a neural network in traversing example points (interpolation) while minimizing error. We will also find out whether activation functions actually affect the convergence rate, or whether this is a property of the optimization algorithm used. As a reference algorithm, we will use a modified population ADAMm that uses elements of stochasticity, and conduct tests with the ADAM built into MLP (classical usage). The latter should intuitively have an advantage, since it has direct access to the gradient of the fitness function surface thanks to the derivative of the activation function. At the same time, the population stochastic ADAMm has no access to the derivative and has no idea at all about the optimization problem surface. Let's see what comes out of this and draw some conclusions.
Author: Andrey Dik