Would you say the Dow Jones is high? Nah... it was higher in july. But compared to ten years ago? Definitely! So a price is obviously meaningless without its context in time. But how can we compare individual small windows like july 2010 to july 2019? I mean the patterns by themselves and not the location of the patterns. The patterns might be identical, but you can't compare them on completely different scales and with a mean and variance that have changed over time. This is one application of stationarity: looking at individual patterns through a peephole. But the trend information is not lost! You can anytime recalculate the original series from the stationary series just by doing all steps in reverse.
After playing around a little with the formula and plotting the results as a graph I wasn't really happy. The amount of stationarity still wasn't well controllable. But I found a good solution:
Let's say the stationary fraction is accounted for by a factor 'd', then we get good control over the scale of its log returns if we chose a factor of (1-d)^2 for the latter, so
fractional_stationary = d * stationary + (1-d)^2*non_stationary
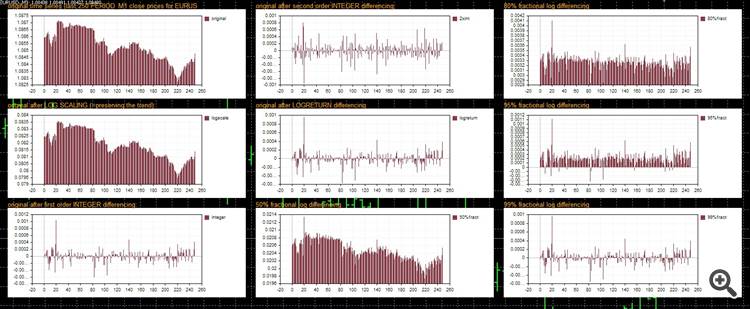
Here you see a little experiment with different stationarity methods and examples with diff. values for d;
I think the graph in the lower middle with d=0.5 shows a good compromise between stationarity and keeping the trend (please also consider the scale and the zero position):
And for those of you who want to see stationarity in action... here's some executable code:
// +------------------------------------------------------------------+ // | stationarity test | // | Metatrader username "Chris70" | // | https://www.mql5.com | // +------------------------------------------------------------------+ #property copyright "metatrader username Chris70" #property version "1.0" #define prices 250 #define curves 9 #define period PERIOD_M1 #include <Graphics\Graphic.mqh> //+------------------------------------------------------------------+ //| global scope | //+------------------------------------------------------------------+ double close[],logclose[],intdiff[],logdiff[],fractdiff[]; int timer=0; CGraphic graph[curves]; color curveclr=clrDarkSlateBlue; datetime lastcalc; //+------------------------------------------------------------------+ //| event handler | //+------------------------------------------------------------------+ void OnInit() { graph[0].Create(0,"original",0,20,20,500,200); graph[1].Create(0,"logscale",0,20,220,500,400); graph[2].Create(0,"1st order diff",0,20,420,500,600); graph[3].Create(0,"2nd order diff",0,520,20,1000,200); graph[4].Create(0,"logreturn",0,520,220,1000,400); graph[5].Create(0,"fractional 50",0,520,420,1000,600); graph[6].Create(0,"fractional 80",0,1020,20,1500,200); graph[7].Create(0,"fractional 95",0,1020,220,1500,400); graph[8].Create(0,"fractional 99",0,1020,420,1500,600); ArraySetAsSeries(close,false); } void OnTick() { if (TimeCurrent()-lastcalc>=PeriodSeconds(period)) { // get close prices array CopyClose(Symbol(),period,0,prices,close); // plot native prices ChartMessage("original time series (last "+IntegerToString(prices)+" "+EnumToString(period)+" close prices for "+Symbol()+"):",0,20,5,10); graph[0].CurveRemoveByName("original"); graph[0].CurveAdd(close,curveclr,CURVE_HISTOGRAM,"original"); // log scaling ChartMessage("original after LOG SCALING (=preserving the trend):",1,20,205,10); ArrayLog(close,logclose); graph[1].CurveRemoveByName("logscale"); graph[1].CurveAdd(logclose,curveclr,CURVE_HISTOGRAM,"logscale"); // first order integer differencing ChartMessage("original after first order INTEGER differencing:",2,20,405,10); stationary(close,intdiff,integer,1); graph[2].CurveRemoveByName("integer"); graph[2].CurveAdd(intdiff,curveclr,CURVE_HISTOGRAM,"integer"); // second order integer differencing ChartMessage("original after second order INTEGER differencing:",3,520,5,10); stationary(close,intdiff,integer,2); graph[3].CurveRemoveByName("2xint"); graph[3].CurveAdd(intdiff,curveclr,CURVE_HISTOGRAM,"2xint"); // logreturn differencing ChartMessage("original after LOGRETURN differencing",4,520,205,10); stationary(close,logdiff,logreturn,1); graph[4].CurveRemoveByName("logreturn"); graph[4].CurveAdd(logdiff,curveclr,CURVE_HISTOGRAM,"logreturn"); // 50% fractional differencing ChartMessage("50% fractional log differencing",5,520,405,10); stationary(close,fractdiff,fractional,0.5); graph[5].CurveRemoveByName("50%fract"); graph[5].CurveAdd(fractdiff,curveclr,CURVE_HISTOGRAM,"50%fract"); // 80% fractional differencing ChartMessage("80% fractional log differencing",6,1020,5,10); stationary(close,fractdiff,fractional,0.80); graph[6].CurveRemoveByName("80%fract"); graph[6].CurveAdd(fractdiff,curveclr,CURVE_HISTOGRAM,"80%fract"); // 90% fractional differencing ChartMessage("95% fractional log differencing",7,1020,205,10); stationary(close,fractdiff,fractional,0.95); graph[7].CurveRemoveByName("95%fract"); graph[7].CurveAdd(fractdiff,curveclr,CURVE_HISTOGRAM,"95%fract"); // 99% fractional differencing ChartMessage("99% fractional log differencing",8,1020,405,10); stationary(close,fractdiff,fractional,0.99); graph[8].CurveRemoveByName("99%fract"); graph[8].CurveAdd(fractdiff,curveclr,CURVE_HISTOGRAM,"99%fract"); for (int n=0;n<curves;n++) { graph[n].CurvePlotAll(); graph[n].Update(); } lastcalc=TimeCurrent(); } } // end of OnTick //+------------------------------------------------------------------+ //| list of differencing methods | //+------------------------------------------------------------------+ enum ENUM_DIFFERENCING { integer=1, logreturn=2, fractional=3 }; //+------------------------------------------------------------------+ //| stationary transformation function | //+------------------------------------------------------------------+ void stationary(double ×eries[],double &target[],ENUM_DIFFERENCING method=integer,double degree=1,double fract_exponent=2) { ArrayResize(target,ArraySize(timeseries)); ArraySetAsSeries(target,false); ArrayCopy(target,timeseries); if (method==integer) { for (int d=1;d<=(int)degree;d++) //=loop allows for higher order differencing { for (int t=ArraySize(target)-1;t>0;t--) { target[t]-=target[t-1]; } ArrayRemove(target,0,1); //remove first element } } if (method==logreturn) { for (int d=1;d<=round(degree);d++) //=loop allows for higher order differencing { for (int t=ArraySize(target)-1;t>0;t--) { target[t]=log(DBL_MIN+fabs(target[t]/(target[t-1]+DBL_MIN))); } ArrayRemove(target,0,1); //remove first element } } if (method==fractional) { for (int t=ArraySize(target)-1;t>0;t--) { double stat=log(DBL_MIN+fabs(timeseries[t]/(timeseries[t-1]+DBL_MIN))); //note: DBL_MIN and fabs are used to avoid x/0 and log(x<=0) double non_stat=log(fabs(timeseries[t])+DBL_MIN); target[t]=degree*stat+pow((1-degree),fract_exponent)*non_stat; } ArrayRemove(target,0,1); //remove first element } return; } //+------------------------------------------------------------------+ //| array log transformation | //+------------------------------------------------------------------+ void ArrayLog(double &arrsource[],double &arrdest[]) { int elements=ArraySize(arrsource); ArrayResize(arrdest,elements); for (int n=0;n<elements;n++){arrdest[n]=log(arrsource[n]);} return; } //+------------------------------------------------------------------+ //| chart message function | //+------------------------------------------------------------------+ void ChartMessage(string message,int identifier=0,int x_pos=20,int y_pos=20,int fontsize=20,color fontcolor=clrOrange) { string msg_label="chart message "+IntegerToString(identifier); ObjectDelete(0,msg_label); //=delete older messages with same identifier (=chose different identifier if older messages shall not be replaced) ObjectCreate(0,msg_label,OBJ_LABEL,0,0,0); ObjectSetInteger(0,msg_label,OBJPROP_XDISTANCE,x_pos); ObjectSetInteger(0,msg_label,OBJPROP_YDISTANCE,y_pos); ObjectSetInteger(0,msg_label,OBJPROP_CORNER,CORNER_LEFT_UPPER); ObjectSetString(0,msg_label,OBJPROP_TEXT,message); ObjectSetString(0,msg_label,OBJPROP_FONT,"Arial"); ObjectSetInteger(0,msg_label,OBJPROP_FONTSIZE,fontsize); ObjectSetInteger(0,msg_label,OBJPROP_ANCHOR,ANCHOR_LEFT_UPPER); ObjectSetInteger(0,msg_label,OBJPROP_COLOR,fontcolor); ObjectSetInteger(0,msg_label,OBJPROP_BACK,false); } void ChartMessageRemove(int identifier=0) {ObjectDelete(0,"chart message "+IntegerToString(identifier));}
That's awesome.
What is this useful for though?
I have recently been trying to scalp ranges using 5 min chart (manual trading) BB period 14 std dev 2 and Lin Reg 300 slope for up trend or down trend and then try to buy low and sell high but still get demolished by the eventual trend that goes against me. I want a way to have a stationary range to buy low and sell high or otherwise a way to protect against the eventual adverse trend conditions.
puh.. there are actually many examples where stationarity is advised or even mandatory, ARIMA / ARFIMA model and neural network inputs are probably the most common scenarios. Anytime when you need to detach a pattern from a long term trend context (that would otherwise distort your statistical metrics). Stationarity returns a distribution with stable variance and mean. It doesn't say much anything about single absolut values or their order within this distribution, so there is still much information and you can always revert a stationary series into non-stationary after you did your statistical metrics (for example: stationary input into a neural network, stationary outputs and labels, then reconverting into prices that a human being understands).
You'll probably need to google a bit...
To start with: https://en.wikipedia.org/wiki/Stationary_process
As you can guess from my current thread about neural networks, I have a rather low opinion about Bollinger Bands in their standard form because the are a combination of two immense problems in trading: the time lag of Moving Averages and standard deviations applied to something that is not even close to being normally distributed.
I'm not really sure what you have in mind / with which method stationarity and BB go together, because anything that's Moving Average bound obviously can't be stationary and if you substract the MA you're just left with the standard deviation.
If you want something better than MA's you might for example want to look into Digital filters, because there are some free "plug and play" examples for download in the codebase and they suffer much less from the time lag problem. Any other good alternative probably has a steeper learning curve (=this is my subjective view).
- en.wikipedia.org
... and the single price method (instead of array operation):
//+------------------------------------------------------------------+ //| single value fractional stationary transformation | //+------------------------------------------------------------------+ void fractdiff(double &t1/*current value*/,double t0/*previous value*/,double fraction=0.5,double fract_exponent=2) { double stat=log(fabs(t1/(t0+DBL_MIN))+DBL_MIN); //note: DBL_MIN and fabs are used to avoid x/0 and log(x<=0) double non_stat=log(fabs(t1)+DBL_MIN); t1=fraction*stat+pow((1-fraction),fract_exponent)*non_stat; return; }or:
double fractdiff(double t1/*current value*/,double &t0/*previous value*/,double fraction=0.5,double fract_exponent=2) { double stat=log(fabs(t1/(t0+DBL_MIN))+DBL_MIN); //note: DBL_MIN and fabs are used to avoid x/0 and log(x<=0) double non_stat=log(fabs(t1)+DBL_MIN); return fraction*stat+pow((1-fraction),fract_exponent)*non_stat; }
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use
Hi traders, - especially those who have some knowledge in statistics -, I'd like to ask you guys about your opinion regarding an alternative method of fractional differencing.
The problem: for many statistical methods we first need to make a time series (/price series) stationary, i.e. transform the data in a way so that mean and variance are stable over time.
The simplest method is just taking the difference (e.g. =today's price minus yesterday's price): x[t] := x[t] - x[t-1]
However, especially over longer time series, stocks and forex prices tend to show exponential instead of linear behaviour, which is why the log difference might be the better choice,
i.e. x[t] := log (x[t] / x[t-1])
I'm aware that the presence of stationarity needs to be confirmed by some kind of "unit root test", like usually the "Augmented Dickey Fuller Test" (ADF).
Let's just assume we have done so... the question still remains if it really is the best idea to aim for perfect stationarity or if sometimes it's better to retain a certain fraction of the trend on purpose.
Here is were fractional differencing comes into play. There has recently been an interesting article, that deals with this subject:
https://www.mql5.com/en/articles/6351
However, the classic method of fractional differencing, also known from the ARFIMA model (https://en.wikipedia.org/wiki/Autoregressive_fractionally_integrated_moving_average),
has some issues dealing with larger sequences, because the denominators quickly reach extremely high numbers. Beyond smaller sequence windows up to ~170 numbers,
we're already running into problems representing those numbers in double precision floating point format. To my knowledge, solutions for this problem do exist, but I also think the classic method is not really
made for many repeated calculations like with every new candle.
This is why a different idea comes to my mind (in this example for log differencing instead of simple differencing, but the idea works for both):
if like stated above
x[t] := log (x[t] / x[t-1]) stands for complete log differencing and
x[t] := log(x[t]) stands for doing almost nothing at all, i.e. only applying log scaling but otherwise preserving the price as is, with the complete trend information,
then
x[t] := d * log(x[t] / x[t-1]) + (1-d)*log(x[t]) should return a mixture of both, depending on the value of "d" (d=real number within range 0-1).
If d=1 we get complete log differencing, whereas for d=0 we keep the initial (log) prices, and for anything in between we get some compromise of the two.
However, the log returns and the logs of the original prices are on a much different scale (the log returns have much smaller values). Therefore it's very hard to guess the impact of the choice for "d",
i.e. what is the absolute value of the right part of the equation, relative to the absolute value of the left part.
So why not just assign a constant that fixates the impact of the right part of the equation, (1-d)*log(x[t]) ? Let's say for example we want the impact of the right part to be a 20% fraction of the left part,
then we can assign a constant, in this example c=0.2 and we know that
(1-d)*log(x[t]) = c * d * log(x[t]/x[t-1])
So which value do we need for d (given this constant fraction for c)?
We divide both sides by d and then by log(x[t]) and get
(1-d) / d = c * log(x[t]/x[t-1]) / log(x[t])
which is the same as
d = 1 / ((c * log(x[t]/x[t-1]) / log(x[t])) +1)
we now can replace d in the original formula with this term and get
x[t] := (1-c) * (1 / ((c * log(x[t]/x[t-1]) / log(x[t])) +1)) * log(x[t] / x[t-1]) + (1-(1 / ((c * log(x[t]/x[t-1]) / log(x[t])) +1)))*log(x[t])
[EDIT: alternative version by adding the term in red]
This equation can possibly be further simplified, but so far it fulfills the objective to assure a fixed impact of the original series onto the stationary log return series.
I'm not sure if there are any specific flaws to this method, so any input is welcome (and I hope I didn't make any mistakes..).
Although I'm totally aware that these are issues most traders don't care about, if anybody has an opinion or critique to this many thanks in advance!!!