Pan PrizMA
- Indikatoren
- Aleksey Panfilov
- Version: 1.3
- Aktualisiert: 23 März 2020
- Aktivierungen: 20
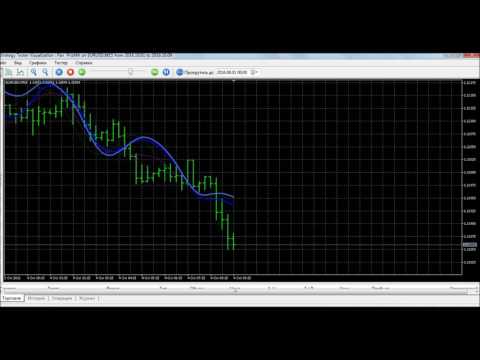
Der Indikator bildet eine gleitende Linie auf der Grundlage einer Interpolation durch ein Polynom mit 1-4 Potenzen und/oder einer Funktion, die aus einer Summe von 1-5 Sinuskurven besteht. Es sind verschiedene Kombinationen möglich, z. B. eine Summe von drei Sinuskurven um eine Parabel zweiter Ordnung. Die sich ergebende Linie kann mit jeder der angegebenen Funktionen und für verschiedene Entfernungen extrapoliert werden, und zwar sowohl als einzelner Punkt bei jedem Indikatorschritt (unveränderliche Linie) als auch als angegebener (neu gemalter) Funktionsabschnitt zur Visualisierung.
Weitere Einzelheiten: https://www.mql5.com/en/market/product/18363#!tab=comments
Der Indikator besteht aus vier Linien. Jede aufeinanderfolgende Indikatorlinie basiert auf den Ergebnissen der vorangegangenen Linie. Jede Linie, mit Ausnahme der ersten, kann in Abhängigkeit von einer bestimmten Richtung gemittelt oder extrapoliert werden
Lineare Interpolation
Für eine Gerade braucht man mindestens zwei Punkte, für eine quadratische Parabel drei Punkte, für eine kubische Parabel vier Punkte, usw. Eine Gerade ist eine arithmetische Progression, die es ermöglicht, nach den ersten beiden Punkten einen dritten zu erhalten: E3 = (E2-E1)+E2 = 2*E2 - E1 ist eine Differenzgleichung erster Ordnung für äquidistante Punkte (ähnlich der Gleichung nach der Reduktion aller Verhältnisse der Lagrange-Gleichung).
Trigonometrische Interpolation
Verwenden Sie die Sinus-Doppelwinkel-Gleichung: Sin 2a = 2 * Cos a * Sin a. Wir können ihre Gültigkeit geometrisch nachweisen als Sin 2a = 2 * Cos a * Sin a - 0 und Sin 3a = 2 * Cos a * Sin 2a - Sin a usw., wobei Cos a ein einstufiger Winkelkosinus ist, während Sin tatsächlich der entsprechende Tabellenwert ist. In diesem Fall sieht eine Differenzgleichung erster Ordnung für die Sinuskurve um Null wie folgt aus: E3 = 2 * Cos a * E2 - E1. Hier sehen wir eine perfekte Analogie zur Geradengleichung. Im Indikator erfolgt der Übergang von trigonometrischen Gleichungen zu linearen Gleichungen, indem die Periode gleich eins gesetzt wird. Cos 360 ist gleich 1, wodurch die Gleichung in eine lineare Gleichung umgewandelt wird.
Externe Variablen (anhand der ersten beiden Zeilen als Beispiel)
- line_1_power =12 - Leistung der interpolierenden Leitung. Bei der trigonometrischen Funktion entspricht die Potenz 2 einer einfachen Sinuskurve um die Konstante. Potenz 3 entspricht einer einfachen Sinuskurve um die geneigte Linie. Die Potenz 4 entspricht entweder einer einzelnen Sinuskurve um die quadratische Parabel oder zwei Sinuskurven um die Konstante, usw. In diesem Fall entspricht die Potenz 12 mit den sechs unten angegebenen Perioden der Funktion, die aus 6 Sinuskurven um die Konstante besteht.
- line_1_leverage =10 - Hebelwirkung der Interpolation. Das Äquivalent der Glättungsperiode. Insbesondere entspricht die Interpolationslinie mit der Potenz eins vollständig dem Standard-EMA mit einem doppelten Periodenwert.
- line_1_interval =1 - Intervall zwischen benachbarten Punkten, die in der Berechnung verwendet werden (nicht zu verwechseln mit dem Leverage). Insbesondere verbindet die gerade Linie drei Punkte (zwei davon sind benachbart, während der verbleibende im Abstand der Hebelwirkung liegt).
- line_1_period_1=6 - Periode der Sinuskurve, wenn die Funktion trigonometrisch ist. Handelt es sich um eine lineare Funktion, wird der Wert 1 festgelegt.
- Zeile_1_Zeitspanne_2=7,5
- Zeile_1_Zeitspanne_3=10
- Zeile_1_Zeitspanne_4=20
- Zeile_1_Zeitspanne_5=60
- Zeile_1_Zeitspanne_6=240
- line_1_shift =0 - Indikator für Linienverschiebung. Standardmäßig werden die Linien unter Berücksichtigung des Leverage Shifts gezeichnet.
- XXXXXXXXXXXXXXXXXXXXXXXXXX1=2 - Trennzeichen für die Parameter der verschiedenen Linien, zur besseren Übersichtlichkeit.
- line_2_trend =1 - Richtung der Linienberechnung: (-1) - Glättung, (1) - Extrapolation.
- line_2_power =10 - interpolierende Linienleistung. Wenn die übrigen Parameter ähnlich wie bei der Glättung sind, verläuft die zweite Linie durch den letzten offenen Punkt des Balkens. Die Potenzen 1001, 1002, 1003-1009, 1010 extrapolieren das Funktionssegment. Das Funktionssegment wird bei jedem Balken neu gezeichnet und ist nur für die Visualisierung notwendig.
- line_2_leverage =8 - Interpolationshebel, bei jedem Wert zeichnet der Indikator einen Punkt im Abstand dieses Hebels, der während der Barbildung nicht neu gezeichnet wird, da er auf dem Eröffnungskurs basiert. Im Falle der Potenzen 1001, 1002, 1003-1009, 1010 wird die gezeichnete Funktionssegmentlinie festgelegt.
Es kann externe Parameterkombinationen geben, die die Linie weit weg vom aktuellen Kurs führen. Am einfachsten ist es, den Anfang eines Charts zu öffnen und die Linie zu untersuchen. Eine Interpolation mit einem Polynom größer als die vierte Potenz ist zum Beispiel mathematisch möglich. Allerdings wächst die Schwingungsamplitude der geglätteten Linie schnell an, was einer Resonanz ähnelt.