Bibliotheken: Statistische Funktionen

Neuer Kommentar
 

Statistische Funktionen:

Eine Reihe von statistischen Funktionen zur Kalkulation einiger Werte zur Beschreibung von Zeitreihen.

Autor: Haruna Nakamura

 
Wie setzen Sie das um?
 
ziad8978:
Wie setzen Sie das um?

Vielen Dank für Ihr Interesse an meiner Bibliothek. Die Anwendung ist sehr einfach, man arbeitet meist mit 1-dimensionalen Arrays.

Zum Beispiel kann man leicht einen linearen Trend aus einer Zeitreihe mit der Funktion detrend entfernen:
detrend(timeSerie, detrendResultArray);

timeSerie ist ein Array, das mit Preisen gefüllt ist, und detrendResultArray sollte ein leeres Array sein, in dem Ihre Ergebnisse gespeichert werden.
Nach dem Funktionsaufruf haben Sie also ein Array mit detrendierten Zeitreihen, auf dem Sie weitere Analysen durchführen können (z. B. prüfen, ob die Reihe stationär ist).

Angenommen, Sie haben ein Array mit der Währung1 (möglicherweise rückwärts), dann können Sie deren nächsten Wert mit prognostizieren:

double detrendedSerie[];
double forecastedValue;

//Währung1 rückwärts speichern (letzter Wert im Array ist der neueste Preis)
detrend(Currency1, detrendedSerie);

if(dickeyFuller(detrendedSerie)){
  forecastedValue = AR1(detrendedSerie); 
}

if(forecastedValue > detrendedSerie[ArraySize(detrendedSerie)-1]){
  //Kaufen
}else{
  //Verkaufen
}

Eine weitere interessante Funktion ist das vorzeichenbehaftete Integral. Die Verwendung in der aktuellen Form ist sehr einfach: Sie rufen die Funktion auf, definieren die Grenzen und den polynominalen Grad (er kann klein sein),
, um eine gute Annäherung an das gegebene Integral zu erhalten. Sie können die Funktion "foo" auch bearbeiten, um andere Funktionen als f(x) = x zu integrieren.

 
ziad8978:
Wie setzen Sie das um?
 
ziad8978:
Wie setzen Sie das um?
 
tinakorn kunchai:
Dateien:
WP_20150602_17_33_10_Selfie.jpg  1287 kb
 
Vielen Dank, Herajika, dass du diesen Code weitergegeben hast!!!
 
Rodrigo Malacarne:
Vielen Dank, Herajika, dass du diesen Code geteilt hast!!!
Freut mich zu hören, dass er Ihnen gefällt! Bitte fügen Sie hier einen Link ein, wenn Sie einen EA/Indikator mit dieser Bibliothek erstellen.
 
Haruna Nakamura:
Freut mich zu hören, dass es Ihnen gefällt! Bitte fügen Sie hier einen Link ein, wenn Sie einen EA/Indikator mit dieser Bibliothek erstellen.

HalloHerajika,

ich versuche, die Dickey-Fuller-Teststatistiken aus dem von dir geteilten Code mit anderer Statistik-/Mathe-Software zu replizieren. Speziell verwende ich Wolfram Mathematica dafür.

Bitte betrachten Sie die Daten aus dem Originalartikel, den Sie verwendet haben (von Scribd):

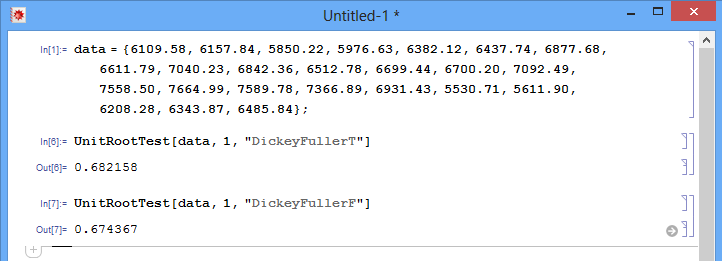
double data[] = {6109.58, 6157.84, 5850.22, 5976.63, 6382.12, 6437.74, 6877.68, 6611.79, 7040.23, 6842.36, 6512.78, 6699.44, 
                 6700.20, 7092.49, 7558.50, 7664.99, 7589.78, 7366.89, 6931.43, 5530.71, 5611.90, 6208.28, 6343.87, 6485.84};

Um die Teststatistiken mit Ihrem Code zu erhalten, habe ich den Kommentar vor der Print-Funktion entfernt, wie im Code unten zu sehen ist:

bool dickeyFuller(double &arr[])
  {
// n=25 50 100 250 500 >500
// {-2.62, -2.60, -2.58, -2.57, -2.57, -2.57};
   double cVal;
   bool result;
   int n=ArraySize(arr);
   double tValue;
   double corrCoeff;
   double copyArr[];
   double difference[];
   ArrayResize(difference,n-1);
//---
   for(int i=0; i<n-1; i++)
     {
      difference[i]=arr[i+1]-arr[i];
     }
//---
   ArrayCopy(copyArr,arr,0,0,n-1);
   corrCoeff=correlation(copyArr,difference);
   tValue=corrCoeff*MathSqrt((n-2)/1-MathPow(corrCoeff,2));
//---
   if(n<25)
     {
      cVal=-2.62;
        }else{
      if(n>=25 && n<50)
        {
         cVal=-2.60;
           }else{
         if(n>=50 && n<100)
           {
            cVal=-2.58;
              }else{
            cVal=-2.57;
           }
        }
     }
   Print(tValue); //--- Teststatistiken ??
   result=tValue>cVal;
   return(result);
  }

Wie gesagt, ich interessiere mich mehr für die Teststatistiken selbst, statt nur für die Schlussfolgerung des Tests. In diesem Sinne erhalte ich mit dem von Ihnen geteilten Code:

void OnStart()
  {
//--- SOURCE: http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#
   double data[] = {6109.58, 6157.84, 5850.22, 5976.63, 6382.12, 6437.74, 6877.68, 6611.79, 7040.23, 6842.36, 6512.78, 6699.44, 
                     6700.20, 7092.49, 7558.50, 7664.99, 7589.78, 7366.89, 6931.43, 5530.71, 5611.90, 6208.28, 6343.87, 6485.84};
//---
   dickeyFuller(data);
  }

Da ich nun die Zeile mit den Teststatistiken ausdrucke, erhalte ich:

-1.719791886975595

Im Originalartikel steht jedoch, dass die t-Statistik 1,8125 beträgt.

Wenn ich jedoch Wolfram Mathematica auf denselben Datensatz anwende, erhalte ich:


Haben Sie eine Idee, was die Ursache dafür sein könnte, dass 3 Tests 3 verschiedene Ergebnisse liefern?

Mit freundlichen Grüßen,
Malacarne

 

Hallo! Was den Unterschied zwischen dem Ergebnis aus dem Artikel(http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#) und meiner Implementierung angeht,
bitte beachten Sie, dass es auf der genannten Website ein Problem mit der Verschiebung von Zeichen (+, -) gibt. Daher ist das im Artikel angegebene Ergebnis -1.8125.

Was den Unterschied zu Wolfram Mathematica angeht, so verwenden die verschiedenen Implementierungen vielleicht unterschiedliche kritische Werte und berechnen die tValues unterschiedlich. Wenn ich das Gleiche in Matlab mache, erhalte ich
ein anderes Ergebnis (0,6518).

Wenn Sie jedoch dasselbe in Excel versuchen, sollte es etwas in der Nähe von -1,8125 anzeigen.

Mit freundlichen Grüßen,
Herajika

 
Haruna Nakamura:

Hallo! Was den Unterschied zwischen dem Ergebnis aus dem Artikel(http://pt.scribd.com/doc/80877200/How-to-do-a-Dickey-Fuller-Test-using-Excel#) und meiner Implementierung angeht,
bitte beachten Sie, dass es auf der genannten Website ein Problem mit der Verschiebung von Zeichen (+, -) gibt. Daher ist das im Artikel angegebene Ergebnis -1.8125.

Was den Unterschied zu Wolfram Mathematica angeht, so verwenden die verschiedenen Implementierungen vielleicht unterschiedliche kritische Werte und berechnen die tValues unterschiedlich. Wenn ich das Gleiche in Matlab mache, erhalte ich
ein anderes Ergebnis (0,6518).

Wenn Sie jedoch dasselbe in Excel versuchen, sollte es etwas in der Nähe von -1,8125 anzeigen.

Mit freundlichen Grüßen,
Herajika

Hallo Herajika,

vielen Dank für die Antwort. Welche Statistik sollte in diesem Fall als die richtige angesehen werden?

Zeigt der Originalartikel falsche Werte für die Teststatistiken?

Mit freundlichen Grüßen,
Malacarne

P.S.: Wenn ich in Mathematica die Option "TestStatistic" nicht verwende, erhalte ich ähnliche Ergebnisse wie in MatLab.

123
Neuer Kommentar