Diskussion zum Artikel "MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 11): Number Walls"
Können Sie bitte diese Tabelle überprüfen:
Wenn ich versuche, dies zu wiederholen, erhalte ich unterschiedliche Ergebnisse:
| Zeile 0 | 0 | 0 | 0 | 0 |
| Reihe 1 | 1 | 1 | 1 | 1 |
| Reihe 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Berechnung. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Zeile 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
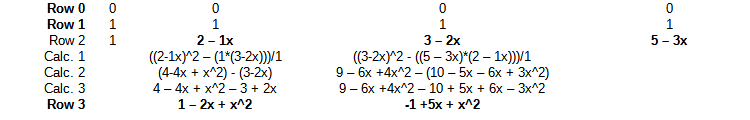
Können Sie bitte diese Tabelle überprüfen:
Wenn ich versuche, dies zu wiederholen, erhalte ich unterschiedliche Ergebnisse:
| Zeile 0 | 0 | 0 | 0 | 0 |
| Reihe 1 | 1 | 1 | 1 | 1 |
| Reihe 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x |
| Berechnung. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | ||
| Calc. 2 | (4-4x + x^2) - (3-2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | ||
| Zeile 3 | 1 - 2x + x^2 | -1 +5x + x^2 |
Hallo,
ich sehe das gerade. Ich schaue es mir mal an und komme zurück.
Pse siehe unten:
Dies ist nicht die Art, wie Identitäten bewiesen werden, aber ich denke, die Algebra ist in Ordnung.
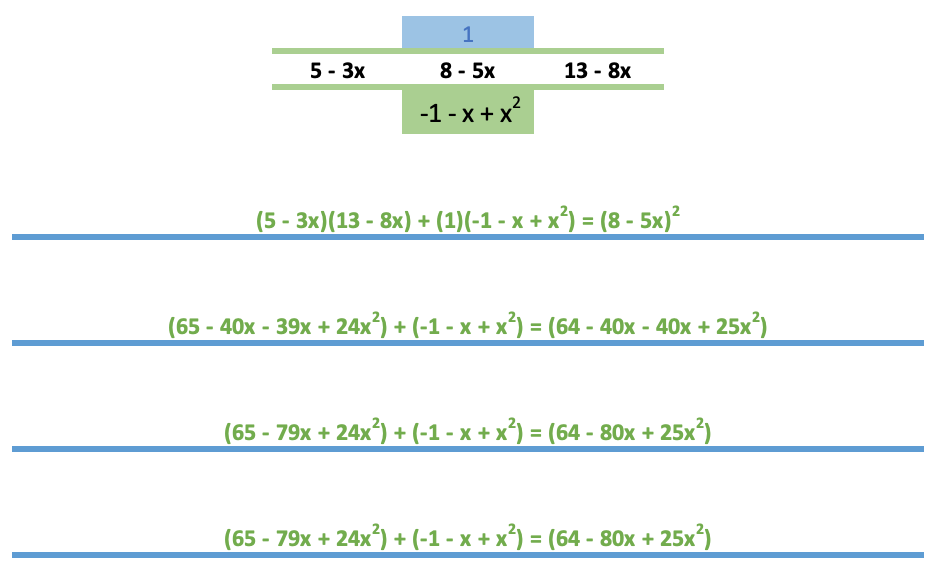
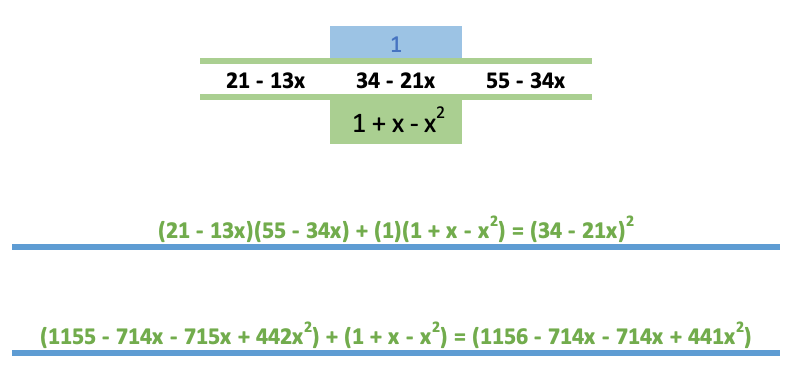
Pse siehe unten:
Dies ist nicht die Art, wie Identitäten bewiesen werden, aber ich denke, die Algebra ist in Ordnung.
Leider nein :(
Es scheint, dass Ihr Beispiel das einzige ist, das funktioniert (brauchen Sie dieses Beispiel wirklich?), siehe hier.
| Zeile 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Reihe 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Reihe 2 | 1 | 2 - 1x | 3 - 2x | 5 - 3x | 8 - 5x | 13 - 8x | 31 - 13x |
| Rechnen. 1 | ((2-1x)^2 - (1*(3-2x)))/1 | ((3-2x)^2 - ((5 - 3x)*(2 - 1x)))/1 | (5 - 3x)^2 - ( (3 - 2x)(8 - 5x)) | (8 - 5x)^2 - (5 - 3x)(13 - 8x) | (13 - 8x)^2 - ( (8 - 5x)(31 - 13x) ) | ||
| Berechnung. 2 | (4 - 4x + x^2) - (3 - 2x) | 9 - 6x +4x^2 - (10 - 5x - 6x + 3x^2) | 25 - 30x + 9x^2 - (24 - 15x +16x + 10x^2) | 64 - 80x + 25x^2 - (65 - 39x - 40x + 24x) | 169 - 208x + 64x^2 - (248 - 104x - 155x + 65x^2) | ||
| Calc. 3 | 4 - 4x + x^2 - 3 + 2x | 9 - 6x +4x^2 - 10 + 5x + 6x - 3x^2 | 25 - 30x + 9x^2 - 24 + 15x - 16x - 10x^2) | 64 - 80x + 25x^2 - 65 + 39x + 40x - 24x) | 169 - 208x + 64x^2 - 248 + 104x + 155x - 65x^2) | ||
| Zeile 3 | 1 - 2x + x^2 | -1 +5x + x^2 | 1 - 31x - x^2 | -1 - 1x + x^2 | -79 - 51x - 1x^2 |
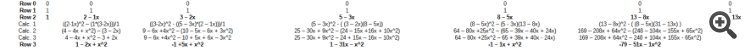
- mathworld.wolfram.com
Ich würde gerne alle durchgehen, aber Sie verstehen schon...
Ja, bis auf die erste Rechnung hast du recht - vielleicht hast du sie unglücklich gewählt.
Bei 1 - 2x + x^2 stimmt es mit deinen alternierenden Ergebnissen von -1 -1x + x^2 und 1 +1x - x^2 überein :(
Ja, Sie haben Recht, außer bei der ersten Berechnung - vielleicht haben Sie sie unglücklich gewählt.
Bei 1 - 2x + x^2 stimmt es mit deinen alternierenden Ergebnissen von -1 -1x + x^2 und 1 +1x - x^2 überein :(
Ähm, du hast gesagt, dass nur eine übereinstimmt, also war das, was ich gerade geteilt habe, eine zweite, die übereinstimmt.
Ich könnte alle durchgehen, aber wenn du meinem obigen Verfahren folgst, solltest du bei allen ähnliche Ergebnisse erhalten.
- 2024.01.31
- MetaQuotes
- www.mql5.com
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Neuer Artikel MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 11): Number Walls :
Number Walls oder Zahlenwände sind eine Variante der Linear Shift Back Registers, die Sequenzen auf ihre Vorhersagbarkeit hin überprüfen, indem sie auf Konvergenz prüfen. Wir sehen uns an, wie diese Ideen in MQL5 von Nutzen sein könnten.
Für einige wenige Zeitreihen ist es möglich, eine Formel für den nächsten Wert in den Sequenzen zu entwickeln, die auf den vorhergehenden Werten basiert, die innerhalb der Sequenz auftraten. Number Walls, Zahlenwände, ermöglichen dies, indem im Vorfeld eine „Zahlenwand“ in Form einer Matrix über die so genannte Kreuzregel erzeugt wird. Bei der Erstellung dieser Matrix geht es in erster Linie darum, festzustellen, ob die betreffende Folge konvergent ist, und der Zahlenwand-Kreuzregel-Algorithmus beantwortet diese Frage gerne, wenn nach einigen Zeilen der Anwendung die nachfolgenden Zeilen in der Matrix nur noch Nullen sind.
In diesem veröffentlichen Artikel, das diese Konzepte aufzeigt, wurde die Laurent Power Series alias Formal Laurent Series (FLS) als Rahmen für die Darstellung dieser Sequenzen mit ihrer Arithmetik im Polynomformat unter Verwendung von Cauchy-Produkten verwendet.
Vergleichende Tests der von den Assistenten zusammengestellten Fachberater sind unten aufgeführt. Beide verwenden das großartige Oszillatorsignal und haben im Prinzip ähnliche Eingänge wie hier angegeben:
Der Unterschied zwischen ihnen besteht darin, dass der eine Experte den Parabolic Sar zum Nachziehen und Schließen offener Positionen verwendet, während der andere den in diesem Artikel vorgestellten Number-Wall-Algorithmus einsetzt. Allerdings unterscheiden sich ihre Berichte trotz des gleichen Signals, wenn sie auf dem EURUSD im letzten Jahr auf dem stündlichen Zeitrahmen getestet werden. Im Folgenden wird zunächst der parabolische Sar-Trailing-Stop-Experte vorgestellt.
Autor: Stephen Njuki