Expert Advisors: Beispiel für die Verwendung eines ONNX-Modells zur Erkennung handgeschriebener Zahlen

Neuer Kommentar
 

Beispiel für die Verwendung eines ONNX-Modells zur Erkennung handgeschriebener Zahlen:

Dieser Expert Advisor handelt nicht. Ein einfaches Panel, das mit der Standard-Canvas-Bibliothek implementiert wurde, ermöglicht es Ihnen, Ziffern mit der Maus zu zeichnen. Das trainierte Modell mnist.onnx wird zur Erkennung von Ziffern verwendet.

Beispiel für die Verwendung eines ONNX-Modells zur Erkennung handgeschriebener Zahlen

Autor: Slava

 
Ich gehe davon aus, dass es beim Trading helfen wird, Chartmuster auf eine andere Art und Weise als ZZ-Muster zu identifizieren, was die Qualität der gefundenen Muster sogar verbessern kann.
 
Ich habe mir die Canvas-Realisierung mit Interesse angesehen, danke. Ist es richtig, dass die Berechnungskomplexität dieses ONNX-Modells für die Bilderkennung gleich der Berechnungskomplexität des Trainings geteilt durch die Anzahl der Trainingsbeispiele ist?
 

Nun. 9er sind weniger gut erkennbar

das macht nichts, denn der Preis dreht sich nicht im Kreis ;)

Es erkennt lineare Ziffern und das ist sehr gut.

kann für die Klassifizierung von Mustern nützlich sein

  

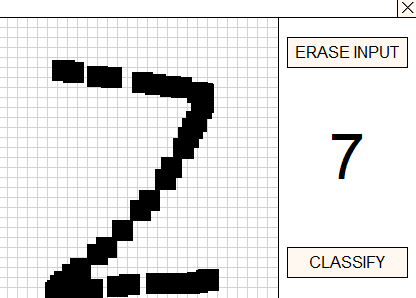
value 7 predicted with probability 0.9998406767845154
Das Modell ist sehr schnell - OnnxRun wird in 100 Mikrosekunden ausgeführt.
 
fxsaber #:
Ist es richtig, dass die Rechenkomplexität dieses ONNX-Modells für die Bilderkennung gleich der Rechenkomplexität des Trainings geteilt durch die Anzahl der Trainingsbeispiele ist?

Ebenfalls geteilt durch etwa 2. Während des Trainingsprozesses wird zusätzlich zur Vorwärtsfunktion die Rückwärtspropagationsfunktion (Backpropagation) aufgerufen.

Ungefähr durch 2 geteilt, weil die Aktivierungsfunktion und die Ableitungsfunktion der Aktivierungsfunktion eine unterschiedliche Rechenkomplexität haben können

 
Slava #:

Ebenfalls geteilt durch etwa 2. Im Lernprozess wird neben der Vorwärtsfunktion auch die Rückwärtspropagationsfunktion aufgerufen.

Ungefähr durch 2 geteilt, weil die Aktivierungsfunktion und die Ableitungsfunktion der Aktivierungsfunktion eine unterschiedliche Rechenkomplexität haben können

Es stellt sich heraus, dass das Training sogar auf einem Kern weniger als 10 Sekunden gedauert hat. Das scheint wirklich schnell zu sein.

Ich frage mich, wie hoch die Anzahl der Gewichte in dem Modell ist. Es ist wahrscheinlich viel primitiver als die neuronalen Netze, die die einfachsten Organismen bewegen.

 
fxsaber #:

Es stellte sich heraus, dass das Training sogar auf einem einzelnen Kern weniger als 10 Sekunden dauerte. Das ist ziemlich schnell.

Ich frage mich, wie viele Gewichte in dem Modell enthalten sind. Es ist wahrscheinlich viel primitiver als die neuronalen Netze, die die einfachsten Organismen bewegen.

Es ist schnell, weil das Modell primitiv ist. Sie müssen auch bedenken, dass das Training nicht in einem Durchgang durchgeführt wird. Mindestens 15 Epochen, wobei jedes Mal 60.000 Bilder durchgemischt werden. Es ist also wirklich sehr schnell.

Die Anzahl der Gewichte zwischen den Schichten ist das Produkt aus den Schichtgrößen. Informationen über mnist.onnx-Schichten finden Sie in netrona

Neuer Kommentar