Bibliotheken: Plattformübergreifende Bibliothek origineller mathematischer Funktionen

Automated-Trading 2017.05.12 13:17

Plattformübergreifende Bibliothek origineller mathematischer Funktionen:

Die verschiedenen Quellen entnommenen originellen mathematischen Funktionen, die entweder einzigartig sind oder viel schneller arbeiten, als alternative Implementierungen.

Tabelle der Entsprechungen den statistischen Funktionen der R Sprache

Nr.	Wert	MQL5 Funktion	Funktion der R Sprache
1	Berechnet das Array für Pearson-Korrelationskoeffizienten	bool MathCorrelationPearson( const double &Signal[], const double &Pattern[], double &Corr[] );	-

Autor: fxsaber

Konstantin 2017.03.27 13:49 #1

Bitte führen Sie den ADF-Test und andere Tests zur Überprüfung der Kointegration durch.

Maxim Dmitrievsky 2017.03.27 15:40 #2

Ein weiteres Goodie von fxsaber, danke )

fxsaber 2017.03.27 18:14 #3

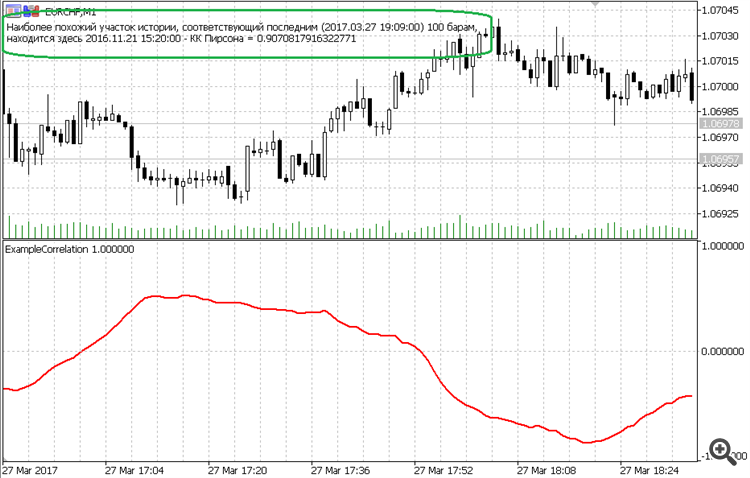
// Der Indikator zeigt den Grad der Ähnlichkeit der einzelnen historischen Intervalle mit dem aktuellen Intervall an

#property indicator_separate_window

#property indicator_buffers 1
#property indicator_plots 1

#property indicator_minimum -1
#property indicator_maximum 1

#property  indicator_color1 clrRed
#property  indicator_type1 DRAW_LINE
#property  indicator_width1 2

sinput int Amount = 100; // Anzahl der letzten Takte (Pattern)

#include <fxsaber\Math\Math.mqh> // https://www.mql5.com/de/code/17982

double Buffer[];

void OnInit()
{
  SetIndexBuffer(0, Buffer);
}

int OnCalculate( const int rates_total,
                 const int prev_calculated,
                 const datetime &time[],
                 const double &open[],
                 const double &high[],
                 const double &low[],
                 const double &close[],
                 const long &tick_volume[],
                 const long &volume[],
                 const int &spread[] )
{
  if (rates_total > prev_calculated)
  {
    double Pattern[];
    
    ArrayCopy(Pattern, open, 0, rates_total - Amount, Amount);
    
    MathCorrelationPearson(open, Pattern, Buffer);
    
    const int Pos = ArrayMaximum(Buffer, 0, rates_total - Amount);
    
    Comment("Der ähnlichste Abschnitt der Geschichte, der dem jüngsten entspricht (" +
          (string)time[rates_total - 1] + ") " + (string)Amount + "Baram, es ist hier." +
          (string)time[Pos] + " - Pearsons IQ = " + (string)Buffer[Pos]);
  }
  
  return(rates_total);
}

Ein Beispiel dafür, wie man schnell das ähnlichste (nach Pearson) Stück der Geschichte finden kann.

Die Stärke der Implementierung liegt nur im Algorithmus - viel schneller als jeder andere.

Aleksandr Slavskii 2017.04.02 18:46 #4

fxsaber:

Ein Beispiel dafür, wie man schnell das ähnlichste (nach Pearson) Stück der Geschichte finden kann.

Die Stärke der Implementierung liegt nur im Algorithmus - viel schneller als jeder andere.

Bei der Geschichte ist das gut. Aber ich würde es gerne andersherum machen, mehrere Bar-Fragmente auf der Geschichte auswählen, und der Indikator benachrichtigt uns darüber, wenn er Übereinstimmungen sieht. Ist eine solche Implementierung prinzipiell möglich?

Über das Ratsmitglied Strategie auf der Grundlage Laguerre-Indikator

fxsaber 2017.04.02 20:18 #5

s22aa:

Was die Historie betrifft, so ist das gut. Aber ich würde es gerne andersherum machen, mehrere Fragmente von Balken in der Historie auswählen, und der Indikator benachrichtigt uns darüber, wenn er Übereinstimmungen sieht. Ist eine solche Implementierung prinzipiell möglich?

Eine einfache Standard-MathCorrelationPearson wird für diese ausreichend sein.

Aleksandr Slavskii 2017.04.03 06:32 #6

fxsaber:
Ein einfacher hauseigener MathCorrelationPearson reicht aus.

Nun, das ist einfach großartig. Ich habe gerade angefangen, C++ in Kursen zu lernen, ich habe schon einige Zyklen hinter mir und fühle mich fast wie ein Programmierguru, na ja, nicht ganz ein Guru natürlich, so halbwegs, eine halbe Gans in einem Wort. Ich denke, in ein paar Jahren wird der Standard MathCorrelationPearson auch für mich "einfach" sein.

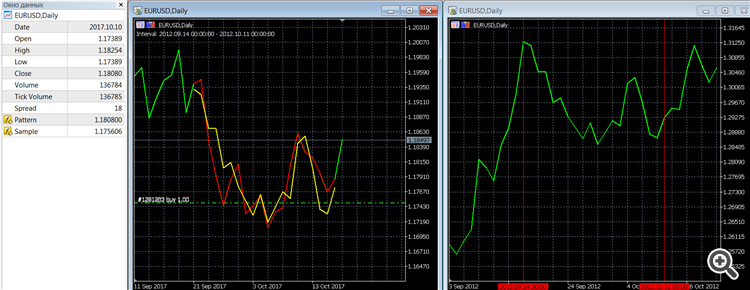
Fehler, Irrtümer, Fragen WARUM VERLIEREN DIE HÄNDLER Maschinelles Lernen im Handel:

fxsaber 2017.10.19 22:16 #7

// Beispiel für die Suche nach dem Intervall, das dem aktuellen Intervall am ähnlichsten ist (QC-Kriterium von Pearson).
#property indicator_chart_window

#property indicator_buffers 2
#property indicator_plots 2

#property  indicator_color1 clrRed
#property  indicator_type1 DRAW_LINE
#property  indicator_width1 2

#property  indicator_color2 clrYellow
#property  indicator_type2 DRAW_LINE
#property  indicator_width2 2

sinput int inAmount = 20;   // Anzahl der letzten Takte (Pattern)
input int  inMaxBars = 1 e5; // Anzahl der zu analysierenden Balken

#include <fxsaber\Math\Math.mqh> // https://www.mql5.com/de/code/17982

double Buffer0[];
double Buffer1[];
double Buffer2[];
int handle;

const long handleChart = ChartOpen(_Symbol, PERIOD_CURRENT);

void OnInit()
{
  SetIndexBuffer(0, Buffer0);
  SetIndexBuffer(1, Buffer1);

  PlotIndexSetString(0, PLOT_LABEL, "Pattern");
  PlotIndexSetString(1, PLOT_LABEL, "Sample");
  
  ChartSetInteger(handleChart, CHART_MODE, CHART_LINE);
  ChartSetInteger(handleChart, CHART_AUTOSCROLL, false);  
}

//------
// Entnommen aus Include\Math\Stat\Math.mqh - https://www.mql5.com/ru/forum/97153/page15#comment_5927026

const double QNaN   =(double)"nan";   // QNaN.

//+------------------------------------------------------------------+
//| Berechnet den Mittelwert der Werte in array[] |
//+------------------------------------------------------------------+
double MathMean(const double &array[])
  {
   int size=ArraySize(array);
//--- Datenbereich prüfen
   if(size<1)
      return(QNaN); // mindestens 1 Beobachtung erforderlich
//--- Mittelwert berechnen
   double mean=0.0;
   for(int i=0; i<size; i++)
      mean+=array[i];
   mean=mean/size;
//--- return mean
   return(mean);
  }
//+------------------------------------------------------------------+
//| Berechnet die Varianz der Werte in array[] |
//+------------------------------------------------------------------+
double MathVariance(const double &array[])
  {
   int size=ArraySize(array);
//--- Datenbereich prüfen
   if(size<2)
      return(QNaN); // mindestens 2 Beobachtungen erforderlich
//--- Mittelwert berechnen
   double mean=0.0;
   for(int i=0; i<size; i++)
      mean+=array[i];
   mean=mean/size;
//--- Abweichung berechnen
   double variance=0;
   for(int i=0; i<size; i++)
      variance+=MathPow(array[i]-mean,2);
   variance=variance/size;
//--- Rückgabe der Varianz
   return(variance);
  }
//------

// Passt Muster zu Muster
void NormalizeArray( const double &Pattern[], double &Sample[], const bool Reverse = false )
{
  const double MeanPattern = MathMean(Pattern);
  const double MeanSample = MathMean(Sample);
  const double Koef = (Reverse ? -1 : 1) * MathSqrt(MathVariance(Pattern) / MathVariance(Sample));
  
  const int Total = ArraySize(Pattern);
  
  for (int i = 0; i < Total; i++)
    Sample[i] = (Sample[i] - MeanSample) * Koef + MeanPattern;
}

void MathLog( double &Array[] )
{
  for (int i = ArraySize(Array) - 1; i >= 0; i--)
    Array[i] = MathLog(Array[i]);
}

void MathExp( double &Array[] )
{
  for (int i = ArraySize(Array) - 1; i >= 0; i--)
    Array[i] = MathExp(Array[i]);
}

// Findet die beste Probe nach Muster
int GetSample1( const int Amount, const double &Prices[], double &Sample[], double &Pattern[], int MaxBars )
{
  const int Total = ArraySize(Prices) - 1; // Entfernen Sie den letzten Balken aus den Berechnungen
    
  ArrayCopy(Pattern, Prices, 0, Total - Amount, Amount);

  MaxBars = (Total > MaxBars) ? MaxBars : Total;
  
  double Prices2[];
  ArrayCopy(Prices2, Prices, 0, Total - MaxBars, MaxBars);  
  MathLog(Prices2);
  
  double Pattern2[];
  ArrayCopy(Pattern2, Pattern);  
  MathLog(Pattern2);
    
  double Pearson[];  
  MathCorrelationPearson(Prices2, Pattern2, Pearson);
  
  const int PosMax = ArrayMaximum(Pearson, 0, MaxBars - Amount);  
  const int PosMin = ArrayMaximum(Pearson, 0, MaxBars - Amount);  
  
  const bool Res = (MathAbs(Pearson[PosMax]) < MathAbs(Pearson[PosMin]));
  const int Pos2 = Res ? PosMin : PosMax;

  ArrayCopy(Sample, Prices2, 0, Pos2 - Amount + 1, Amount);
  NormalizeArray(Pattern2, Sample, Res);  
  MathExp(Sample);
      
  return(Pos2 + Total - MaxBars);
}

void OnDeinit( const int )
{
  ChartClose(handleChart);
}

int OnCalculate( const int rates_total,
                 const int prev_calculated,
                 const datetime &time[],
                 const double &open[],
                 const double &high[],
                 const double &low[],
                 const double &close[],
                 const long &tick_volume[],
                 const long &volume[],
                 const int &spread[] )
{
  if (rates_total > prev_calculated)
  {       
    double Pattern[];
    double Sample[];
    
    const int Pos = GetSample1(inAmount, close, Sample, Pattern, inMaxBars);   
    
    // Wir haben das Muster selbst abgeleitet
    ArrayInitialize(Buffer0, EMPTY_VALUE);
    ArrayCopy(Buffer0, Pattern, rates_total - inAmount - 1);

    // Beispiel ausgeben
    ArrayInitialize(Buffer1, EMPTY_VALUE);
    ArrayCopy(Buffer1, Sample, rates_total - inAmount - 1);
    
    Comment("Interval: " + (string)time[Pos - inAmount + 1] + " - " + (string)time[Pos]);
  
    // Anzeigen des gefundenen Abschnitts
    const int Offset = 10;
    ChartNavigate(handleChart, CHART_BEGIN, Pos - inAmount + 1 - Offset); // Verschiebung des Diagramms um Offset-Takte vor dem Beginn der Sample-Quelle
    ObjectCreate(handleChart, "Left", OBJ_VLINE, 0, time[Pos - inAmount + 1], 0);
    ObjectCreate(handleChart, "Right", OBJ_VLINE, 0, time[Pos], 0);    
  }
  
  return(rates_total);
}