R = e^(-(2*a*z)/(d*d))
Where:
R = risk of losing z fraction of the account
e = 2.71828, the base of the natural logarithm
z = The fraction of the account that might be lost, inthiscase10%, or 0.10
a = average, or mean return, inthiscase6.5%, or 0.065
d = standard deviation of returns, inthiscase10.47%, or 0.1047
因此,我们计算出你的R(你可以预期你的账户在100次交易后下降10%的频率)为:
R = 2.71828^(-(2*0.065*0.10)/(0.1047*0.1047))
R = 0.30547
R = 30.5%
R = (1-z)^(-2*a/(d*ln(1-d)))
Where:
R = risk of losing z fraction of the account
z = The fraction of the account that might be lost, inthiscase10%, or 0.10
a = average, or mean return, inthiscase6.5%, or 0.065
d = standard deviation of returns, inthiscase10.47%, or 0.1047
因此,我们计算建立在你所开发的交易策略基础上的复利交易方法的R,我们得到:
R = (1-z)^(-2*a/(d*ln(1-d)))
R = (1-0.10)^(-2*0.065/(0.1047*ln(1-0.1047)))
R = 0.3064
R = 30.6%
我试图理解你的x和P(x)数字的来源,我想也许英语不是你的第一语言,所以我想在我做出任何结论或混乱的陈述之前,确保我们理解你所使用的术语的含义。
"每笔交易有0.5%的恒定风险"
什么是每笔交易0.5%的风险?这是否意味着在市场走势不利于你的头寸且头寸以止损价平仓的情况下,你要承担账户余额的0.5%的风险?
"这意味着我有0.35%的机会处于账户余额的50%"
毁约风险是一种时间因素的计算,意味着你用你计算的数字在报表上的单位是 "每笔交易 "或 "每周 "或 "每月"。
目前,我无法知道x和P(x)来自哪里,但这决定了这里涉及的单位。
帮助我理解你的做法,我很乐意投入时间来确定你是否正确应用了计算方法。
嗨,菲利普
谢谢你在这里帮助我 :)
每笔交易0.5%的风险正是这个意思。是指如果市场对我的头寸不利并达到SL,我所损失的金额。
0.35%的数值是整个测试期间的数值(大约是8年....),X和P(X)也都取自这份报告。
我真的搞不清楚在什么时间段内进行这种计算是合乎逻辑的!
让我们以2001年1月10日至2002年1月10日为例。
计算这段时间的系数是否符合逻辑呢?这里有足够的数据来确定胜利和失败交易之间的关系吗...?
希望我这次说得很清楚 :)
你使用毁灭风险计算的方式是你定义一个时间段(月、周、年等),或某种增量(每笔交易、每10笔交易等),然后你对这些时间段的统计数据进行汇总。 就毁灭风险计算的结果输出的实际含义(其单位)而言,这很重要。
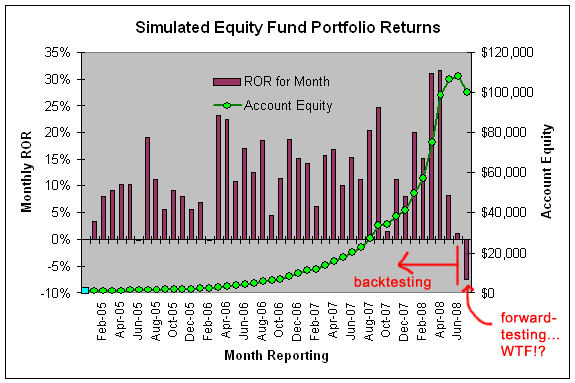
有时,首先要集中精力确保你问的问题是正确的(换句话说,确保你试图计算的答案实际上是要回答你需要/想要回答的问题)。
例如,我的客户在每月的时间轴上运作。 他们不关心每天或每周的事情,对他们来说,所有的都是每月的结果。 因此,在我的案例中,我计算每周结果或每笔交易的毁灭风险对任何人都没有好处。
因此,我在回测中必须做的是捕捉每月的平均回报率(利润、损失、ROR等)。 类似于下面这样的情况。
为了计算毁坏风险指标,你必须首先收集你的时间框架的数据。 在我这个例子中,我需要收集月度回报率的结果,计算平均月度回报率,然后计算这些月度回报率的标准差。
在这个例子中,平均月回报率为12%,标准差为8%......从回测结果来看,这应该是未来的黄金,但事实并非如此(如你所见)。 请注意,我把毁坏的风险称为损失的风险(ROL),因为我对知道我的账户何时会被毁坏不感兴趣(这是一个微不足道的问题),而我更感兴趣的是知道我应该多频繁地预期账户会被某个固定数额的资金淹没,例如20%。
因此,12%的月回报率和8%的标准偏差意味着我可以预期我的账户在6.5%左右的时间里会出现7.4%的账户价值损失(6.5%的月末事件,或者大约每15个月一次)。
因此,虽然我最初被这个看似莫名其妙的正向测试结果弄得措手不及,但根据回测结果,预期这样的月度结果是完全合理的,一旦非常15个月,我可以预期我账户的高水位会出现这样的负缩水。
所以你看,为了让你计算出一个有意义的损失风险评估,你必须首先决定什么时间段与你有关,然后你必须把结果集合起来,以利于计算该时间段的平均和标准偏差的RoR。
一旦你有了回测的数据,你就可以用毁灭风险(或我喜欢的损失风险)计算来进行无数基于统计的分析。
我有很多问题!!
for starters....
1- 在你的月度计算中,你是否假设头寸大小不变?
2- 每个月的测试都是在初始存款的基础上进行的吗? 不管前几个月的进展如何?
假设前两个问题的答案是YES :)
我计算了14组100个交易的ROR值
我使用0.01手的大小,以每组700美元的初始存款进行计算
并得到以下结果。
(我需要安装EXCEL,不是吗...?)
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
从这些数据中,我得到的平均ROR为6.5%,标准偏差 为10.47%。
现在我不确定如何计算第二部分。
"因此,12%的月回报率和8%的标准偏差意味着我可以预期我的账户在6.5%左右的时间里经历7.4%的账户价值损失(6.5%的月末事件,或者大约每15个月一次)。
我有很多问题!!
for starters....
1- 在你的月度计算中,你是否假设头寸大小不变?
2- 每个月的测试都是在初始存款的基础上进行的吗? 不管前几个月的进展如何?
是的,如果你想消除分析中的事件时间偏差,回测必须始终在没有复利的情况下进行。 如果我们打算采用非加权的统计分析(如取平均值和标准差 等),我们必须将每个事件(交易)放在与其他事件同等的权重上。 我怀疑你已经意识到了这一点。
当正向测试/实时测试时,你必须做出选择--你是想让正向测试都是为了赚钱(那时复利应该是有效的),还是想让正向测试进一步产生可用于这些类型的统计分析的数据?
我应该注意到,在抽样期变得足够小的数学极限中,统计偏差因素会变成统一(1),所以在这些情况下,忽视统计偏差生效的事实所带来的误差可能是最小的。
所有这些胡言乱语的意思是说,你必须做出决定,既要考虑到你的回测,也要考虑到你的正向测试(或真实交易),如果你希望两者之间的统计数据在数学意义上具有可比性,那么你需要确保你管理回测的方式,使结果数据可以映射(另一个数学术语)到正向测试的相关统计数据上。
用固定的手数来做回测,而不考虑起始账户的余额,这是回测的唯一方法。
假设前两个问题的答案是YES :)
我计算了14组100个交易的ROR值
我使用0.01手的大小,以每组700美元的初始存款进行计算
并得到以下结果。
(我需要安装EXCEL,不是吗...?)
1-> 0%
2-> + 12%
3-> 0%
4-> + 18%
5-> - 3%
6-> -8%
7-> +22%
8-> -3%
9-> +11%
10-> +23%
11-> +17%
12-> +7%
13-> -8%
14-> +2%
从这些数据中,我得到的平均ROR为6.5%,标准偏差为10.47%。
现在我不确定如何计算第二部分。
"因此,12%的月回报率和8%的标准偏差意味着我可以预期我的账户在6.5%左右的时间里经历7.4%的账户价值损失(6.5%的月末事件,或者大约每15个月一次)。
一旦你有了回测 的数据,并且只要数据是按照上面的帖子中讨论的那样准备的,你就可以选择你想用哪一个方程式来计算你未来的损失风险。你是否会使用复利?如果你不打算使用复利,那么公式很简单,如下所示:
因此,我们计算出你的R(你可以预期你的账户在100次交易后下降10%的频率)为:
因此,在这个例子中,问题是 "在100次交易后,我可以预期我的账户从高水位下降至少10%的频率是多少?"答案是 "30.5%的时间会发生这种情况"。
或者反过来说,你可以说 "我的账户应该至少每三个100次交易期从高水位线下降10%"。这是在你不做复利的情况下。
如果你打算在你的账户中做复利,用于远期测试或现场测试,那么你使用相同的RoR%和stand-dev(因为你生成它们时没有事件年表,它们也可以映射到这种用途),那么你只需使用更复杂的论坛程序:
因此,我们计算建立在你所开发的交易策略基础上的复利交易方法的R,我们得到:
在这种情况下,复利或不复利对计算出的损失风险没有什么区别(30.6%对30.5%),正如预期的那样,但如果你的夏普比率<1,复利的表现总是比不复利差(至少在统计上)。
我不确定我们是否在同一起跑线上......。
这些公式是非常熟悉的......。
然而,对于手中的价值分配,有30.5%的机会失去至少10%的账户余额,这真的有意义吗?
考虑到这组14个数值的最大跌幅是8%,而且只重复了两次,从未低于8%!?
因此,30.5%的缩减10%以上的比例似乎很不合适......
我做了自己的小研究,并试图计算出现10%以上缩水的几率,得到了一个不同的结果
我使用了以下公式。
X是一个正态分布的随机变量,平均值为μ,标准差 为σ。
X= - 10%
µ= 6.5%
σ = 10.47%
由于正态分布的对称性,我可以使用+1.576
到Z为止的累积概率由 ->Φ(t)=P(Z≤t)
但我需要计算互补累积,即1-Φ(t)=1-P(1.576)=1-0.9418=0.0582=5.8%。这有什么意义吗?我们说的是同一件事吗?
X是正态分布中的一个随机变量,平均值为μ,标准差为σ。
X= - 10%
µ= 6.5%
σ = 10.47%
但我需要计算互补累积,即1-Φ(t) = 1 - P(1.576) = 1 - 0.9418 = 0.0582 = 5.8%。这有什么意义吗?我们谈论的是同一件事吗?
这里的μ 是平均缩水还是平均收益率?而这里的σ 是缩减的标准差还是RoR的标准差?补充累积是指10%的缩减概率还是-10%的收益率的概率?
按照我的理解,你是把你的收益 风险值和缩减 风险值混为一谈。如果你想计算缩减风险的统计数据,那么你需要计算每笔交易的缩减(不是利润/亏损,而是交易 "活 "的时候的瞬时缩减),这样你就可以计算每笔交易的平均缩减和stddev,然后互补的累积值将代表你所想的。
我们谈论的是毁灭的风险(特别是损失的风险,是毁灭的风险计算的一个更普遍的情况)。看看这篇文章,我的意思是真的读一读,而不是仅仅敷衍一下所采用的具体词汇的细微差别。
在第二页,我们有一个非常简单的计算方法,用于计算失去1西格玛的风险,你的西格玛是10.47%。损失10.47%的风险取决于你的平均收益率,你的情况是6.5%。你的sharpe低于1(通常不被认为是好事),你损失10.47%(1-西格玛)的风险是29.1%。
请注意这个图表的序数和负数,人们经常被这个问题绊倒。y轴应该在你的脑海中激发出几个关键问题,回答这些问题将引导你走上理解缩水的道路。问自己 "为什么我有接近100%的概率发生0.1%的损失?"。
想一想,想一想我们用损失/损失风险计算的是什么,想一想你的交易的资产与时间曲线图是什么样子的,并认识到每次它创下新高,然后稍稍回撤,这种稍稍的回撤就是从新设定的高水位线开始缩减。
无论如何,人们并不倾向于考虑1-西格玛的损失风险,他们确实倾向于以50/50的方式思考,就像抛硬币。那么,你的账户在50%的时间里会损失多少资产呢?答案是。6%
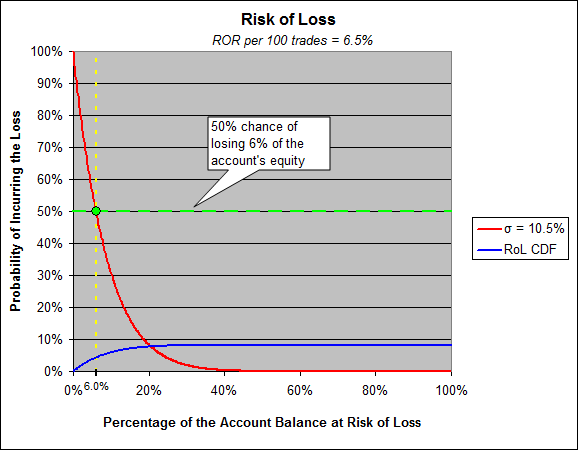
你有50/50的机会在任何特定的100轮交易结束时损失6%。
同时要明白,这个计算是基于仅仅14个样本的统计,通常我们把这些计算得出的数字称为 "下限"。意思是说,当我们计算出你在50%的时间里会损失你账户资产的6%时,我们也认为这个数值实际上意味着 "至少6%,但由于未计算的风险因素,可能更高"。
75%的人在外汇中亏损是有原因的,尽管回测显示他们的策略是圣杯。数据在他们手中(也就是说,他们可以根据需要生成数据),可以计算出毁掉的风险,但他们被卖给了希望和梦想,即利润因素和预期回报等。
不过,不要相信我的话,你已经得到了这篇文章,可以去找大卫问问,他喜欢谈论这个话题。并对它进行测试。把你的回测策略放到正向测试中,看看会发生什么。(你看了我上面的结果吗,当我自己无意中做了这个实验?)
(在损失风险分析中还有一个金融顿悟的小插曲,你会发现为什么夏普比率在金融分析师中如此受人尊敬,然后你就会意识到它的主要弱点,以及为什么人们说 "贝塔会杀人")
好的
我想我明白了,谢谢
明天我会带着更多的问题回来 :)
哦......。
有一件事我还是不明白....,难道就没有任何其他因素影响这个计算吗?
让我们来看看你按月计算的ROR结果吧
让我们假设(为争论起见),一个月内的交易越多,你的ROR就越高
例如:0次交易,你赚0%。
10笔交易,你赚取5%(平均)
20笔交易,你可以赚到10%(平均)。
以此类推...
让我们假设在这30个月里,在ROR分布中存在一个很高的数值分布(每个月都有完全不同的交易数量)。
因此,平均回报率为10%,标准偏差 为20%,没有负的ROR(你不可能有负的交易数量......)。
现在计算一个标准差的损失风险,也就是20%,我们会得到大约37%......这真的没有任何意义。
你知道我在说什么吗?