为什么在学位方面会有这样的花招？ - 页 2

[Andrey Azatskiy]

Roman:

-0.2不为零返回除以零 的错误。

该函数返回-nan，即不是一个数字。当试图除以-nan时，会出现错误。如果有的话，错误的文字就是不合适。

[[删除]]

正确的解决方案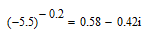： ，解决方案是在复数领域。

但如果我们谈论的是对正负输入参数有不同的解决方案分支，我们只需要先定义这些分支。

.

做出这样的功能，你就可以了。）

[Roman]

Andrey Azatskiy:

该函数返回-nan，即不是一个数字。当试图除以-nan时，会出现一个错误。如果有的话，错误的文字就是不合适。

究竟为什么-0.2会是-南？）

另一个测试功能

在计算器中。

1/(-3 ^ 3)

-27

在mql函数中

double n = 1.0/MathPow(-3.0, 3.0);
Print(n);

-0.03703703703703703

[Andrey Azatskiy]

Roman:

那么，到底为什么-0.2是一个南？）

另一个测试功能

在一个计算器中

在一个mql函数中。

不是-0.2-南，而是度数增加的结果。
一个数字的分数度（a^m/n）是a^m的n度根。
如果子根值是负的，它可以是负的或正的，基于m的幂和数字a本身（在我的问题中它总是负的，所以它在m的正幂时是正的，在负幂时是负的）。因此，如果子根值是负的，那么这个数字也是负的。负数的根在复数区，所以我们不能通过通常的双数类型 对复数区的值进行操作，这就是为什么度的标准实现会给出-nan。

[Andrey Azatskiy]

Олег avtomat:

正确的解决方案：解决方案是在复数领域。

但如果我们说的是对正负输入参数有不同的解决方案分支，那么我们只需要先定义这些分支。

.

做出这样的功能，你就可以了。）

谢谢你的详细回答。但对我来说，复数微积分不适合我的问题，所以很可能我将把自己限制在自然数上，结果是我不会落入复数领域。

[[删除]]

Andrey Azatskiy:

谢谢你的详细答复。但对我来说，复杂的微积分不适合我的问题，所以我可能会把自己限制在自然数上，结果是我不会落入复杂的领域。

这就是我所说的，我特别给你看了一个例子。仔细看一下。这个例子正是针对你的情况。

zy

翻译成µl是非常容易的

[Roman]

Andrey Azatskiy:

不是-0.2-南，而是一个学位的结果。
一个小数的幂（a^m/n）是a^m的n度根。
如果子根值是负的，根据m的幂数和数字a本身（在我的问题中，a总是负的，所以它在m的正幂时是正的，在负的时是负的），它可以是负的或正的。因此，如果子根值是负的，那么这个数字也是负的。负数的根在复数区，所以我们不能通过通常的双数类型 对复数区的值进行操作，这就是为什么度的标准实现会给出-nan。

安德烈，是的，我说错了，很明显，提高到一个幂的结果是返回-南。
但这一结果产生了一个分数幂，其中整数为零-0.2
计算器的计算结果都是正确的。

而之前的测试，也不像计算器里那样算数。

[Andrey Azatskiy]

Олег avtomat:

这就是我所说的，我特别给了你一个例子。好好看看吧。

是的，我知道了，谢谢你。(连公式都写下来了)

[Aleksey Nikolayev]

Andrey Azatskiy:

也许这条腿是由于你不能从一个负数中提取偶数根而产生的？我已经有点糊涂了......最重要的是，如何绕过它？

整数的确定只需通过乘法（对负指数取反），所以可以很容易地转移到负数的基础上。分数度通过对数和指数来定义：y^x=exp(x*ln(y))，带着负数来到复平面。对数有无限多的分支，为了避免寻找正确分支的麻烦，他们返回NAN。

[Igor Makanu]

Andrey Azatskiy:

谢谢你的回答，但一般来说，如果我们采取算术上正确的解决方案，似乎只有复数可以用来实现这样的解决方案......。在你提出的方法中，有必要打破度数，使基础值总是有一个正的度数，答案将总是正的。但是，如果你不考虑这种拟合--我们只想到复数，因为根据我所知的普遍接受的代数模型（我不是数学家）--一个负数的根将是一个复数。

使用我上面建议的公式。

下面是同样的公式。

void OnStart()
  {
   int m = 2;
   int n = 10;
   
   double result = 1.0/pow(pow(-5.5,m),1.0/n); 		// result = 0.7110947333604484
   Print("result = ",result);
  }

下面是一个如何将双数转换成分数的例子

https://www.mql5.com/ru/forum/290279#comment_9396706