SB图能否与价格图区分开来? - 页 6 12345678910111213...28 新评论 Violetta Novak 2018.09.19 09:39 #51 Vizard_:是的,但只是在联想的层面上。这些图表是高度压缩的。猜谜游戏)))。 猜测或不猜测,新星会告诉我们......我将暂时折磨大家))。 Violetta Novak 2018.09.19 09:40 #52 sibirqk: 它仍然很美!哦,尽我所能,我知道左和右))。 Даниил Минин 2018.09.19 09:48 #53 Novaja:这里danminin 写道,差别只在峰度上,也就是在岛度上,由此可见,大量的小增量,为什么会出现这种情况,而TSP却没有得到满足?这些是更多的增量,而不是在sb上。 这些都比较少。 又有更多这样的人。 Georgiy Merts 2018.09.19 10:46 #54 Maxim Dmitrievsky:哪里有反驳说引文是随机的?而哪里能证明引文的整个生命过程最终不会趋于正常?而你首先是在什么维度上测量的呢?) 又有谁说我们有一个无限的随机过程,一定会收敛到正常的我很久以前就经历过这个阶段。我试图使市场 "正常化"。我计算了各种指标,进行了假设测试......。我总是在0.9或更高的显著性水平上得出一个结论--价格运动在任何地方都不正常。 高斯极限定理说,如果一个随机变量取决于大量的独立变量--它的值在极限中由正态法描述。 这就是重点,我们的随机过程--永远不会收敛到正常。最多--它只能在一段时间内与正态分布相吻合。 Georgiy Merts 2018.09.19 10:50 #55 Dmitry Fedoseev:假设我们抛出一枚硬币,如果是正面就是正面,如果是反面就是反面。再抛出5个硬币,如果都是头,我们就在第一个硬币的基础上加5分--这是一种新闻模拟,直到出了三只老鹰。将会有一个波动的高峰。这里的异常在哪里?为什么这样的过程在现实市场中是不正常的?好吧,你所模拟的只是一个正常的随机过程,因为硬币的翻转取决于大量的独立因素。检查 分布均匀性的假设--你可能会确认,在较高的显著性水平下,掷硬币是一个均匀的随机过程。 另一方面,实际的价格运动是一个完全不同的过程。而且它不能用均匀分布来描述,也不能用正态分布来描述--同样,因为价格不受独立因素的影响。 Igor Makanu 2018.09.19 10:54 #56 Georgiy Merts:这就是问题所在--我们的随机过程--永远不会收敛为一个正常的过程。最多只能在一段时间内与正态分布相吻合。有人把价格的变动比作汽车的速度,我认为这是一个很好的例子--在某些时间点上,汽车的速度服从加速定律,然后它可以停止,然后它可以转弯。 无论你怎么努力,汽车速度的规律是无法用数学公式来描述的。 有@Maxim Dmitrievsky的 说法,非随机过程必须是周期性的,嗯,这不是非随机性的 "必要条件"...指数的同一图形不是周期性的,但也不会是随机的 [删除] 2018.09.19 10:57 #57 一个在树林里,一个在树林外...... 我强烈推荐你阅读它。 Ventzel E.S., Ovcharov L.A. 概率论及其工程应用莫斯科: Nauka.1988年(工程师的物理和数学图书馆)。- 480 с. 从实际应用的角度系统阐述概率论的基础,包括:控制论、应用数学、计算机、自动控制系统、机制理论、无线电工程、可靠性理论、运输、通信等专业。尽管这些应用涉及到不同的领域,但它们都被一个共同的方法论框架所渗透。 适用于广泛的工程师和不同背景的科学家,他们在实际活动中面临着设置和解决与随机现象有关的问题的需要。大学生和相关专业的教师也可使用该书。 . 并从头开始阅读。 sibirqk 2018.09.19 10:58 #58 Novaja:哦,尽我所能,我知道左和右))。我是指Vizard_的 照片。 Dmitry Fedoseev 2018.09.19 11:09 #59 Georgiy Merts:所以你是在为一个正常的随机过程建模,因为硬币的翻转取决于大量的独立因素。检验分布均匀性的假设--你大概可以确认,在高度显著的情况下,掷硬币是一个均匀的随机过程。 另一方面,实际的价格运动是一个完全不同的过程。而且它不能用均匀分布来描述,也不能用正态分布来描述--同样,因为价格不受独立因素的影响。你如何确定它是一个完全不同的过程? [删除] 2018.09.19 11:10 #60 Igor Makanu:有人把价格的变动比作汽车的速度,我想这是一个很好的例子--在某些时间点,汽车的速度服从加速定律,然后它可能会停下来,然后可能会有一个转弯。 无论你怎么努力,汽车速度的规律是无法用数学公式来描述的。 有@Maxim Dmitrievsky的 说法,非随机过程必须是周期性的,嗯,这不是非随机性的 "必要条件"...指数的同一图形不是周期性的,但也不会是随机的一个非随机过程可能有一个线性趋势或一个周期性趋势。但仍然必须有一些东西将这个过程定性为非随机的,否则它就是一个具有任何分布密度的SB 如果不能区分恒定成分,那么这个过程当然是随机的,有什么可想的呢? 一个随机的过程可以假装非随机的,是偶然的。这就是为什么在市场上经常有一种错觉,认为它是可以预测的,但随后这个时期过去了,所有的信号都合并了 12345678910111213...28 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
是的,但只是在联想的层面上。这些图表是高度压缩的。猜谜游戏)))。
猜测或不猜测,新星会告诉我们......
我将暂时折磨大家))。
它仍然很美!
哦,尽我所能,我知道左和右))。
这里danminin 写道,差别只在峰度上,也就是在岛度上,由此可见,大量的小增量,为什么会出现这种情况,而TSP却没有得到满足?
这些是更多的增量,而不是在sb上。
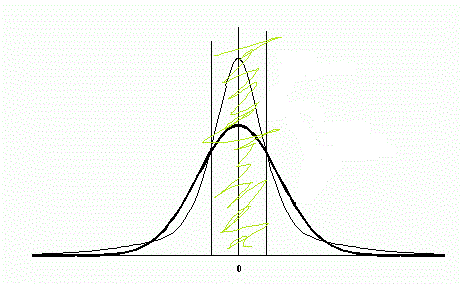
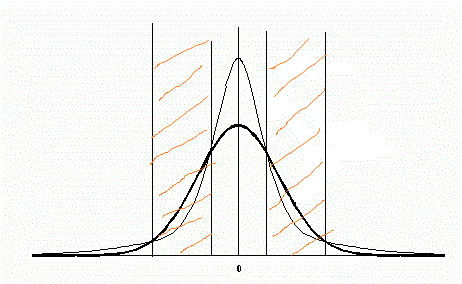
这些都比较少。
又有更多这样的人。
哪里有反驳说引文是随机的?而哪里能证明引文的整个生命过程最终不会趋于正常?而你首先是在什么维度上测量的呢?)
又有谁说我们有一个无限的随机过程,一定会收敛到正常的我很久以前就经历过这个阶段。我试图使市场 "正常化"。我计算了各种指标,进行了假设测试......。我总是在0.9或更高的显著性水平上得出一个结论--价格运动在任何地方都不正常。
高斯极限定理说,如果一个随机变量取决于大量的独立变量--它的值在极限中由正态法描述。
这就是重点,我们的随机过程--永远不会收敛到正常。最多--它只能在一段时间内与正态分布相吻合。
假设我们抛出一枚硬币,如果是正面就是正面,如果是反面就是反面。再抛出5个硬币,如果都是头,我们就在第一个硬币的基础上加5分--这是一种新闻模拟,直到出了三只老鹰。将会有一个波动的高峰。这里的异常在哪里?为什么这样的过程在现实市场中是不正常的?
好吧,你所模拟的只是一个正常的随机过程,因为硬币的翻转取决于大量的独立因素。检查 分布均匀性的假设--你可能会确认,在较高的显著性水平下,掷硬币是一个均匀的随机过程。
另一方面,实际的价格运动是一个完全不同的过程。而且它不能用均匀分布来描述,也不能用正态分布来描述--同样,因为价格不受独立因素的影响。
这就是问题所在--我们的随机过程--永远不会收敛为一个正常的过程。最多只能在一段时间内与正态分布相吻合。
有人把价格的变动比作汽车的速度,我认为这是一个很好的例子--在某些时间点上,汽车的速度服从加速定律,然后它可以停止,然后它可以转弯。
无论你怎么努力,汽车速度的规律是无法用数学公式来描述的。
有@Maxim Dmitrievsky的 说法,非随机过程必须是周期性的,嗯,这不是非随机性的 "必要条件"...指数的同一图形不是周期性的,但也不会是随机的
一个在树林里,一个在树林外......
我强烈推荐你阅读它。
Ventzel E.S., Ovcharov L.A.
概率论及其工程应用
莫斯科: Nauka.1988年(工程师的物理和数学图书馆)。- 480 с.
从实际应用的角度系统阐述概率论的基础,包括:控制论、应用数学、计算机、自动控制系统、机制理论、无线电工程、可靠性理论、运输、通信等专业。尽管这些应用涉及到不同的领域,但它们都被一个共同的方法论框架所渗透。
适用于广泛的工程师和不同背景的科学家,他们在实际活动中面临着设置和解决与随机现象有关的问题的需要。大学生和相关专业的教师也可使用该书。
.
并从头开始阅读。
哦,尽我所能,我知道左和右))。
我是指Vizard_的 照片。
所以你是在为一个正常的随机过程建模,因为硬币的翻转取决于大量的独立因素。检验分布均匀性的假设--你大概可以确认,在高度显著的情况下,掷硬币是一个均匀的随机过程。
另一方面,实际的价格运动是一个完全不同的过程。而且它不能用均匀分布来描述,也不能用正态分布来描述--同样,因为价格不受独立因素的影响。
你如何确定它是一个完全不同的过程?
有人把价格的变动比作汽车的速度,我想这是一个很好的例子--在某些时间点,汽车的速度服从加速定律,然后它可能会停下来,然后可能会有一个转弯。
无论你怎么努力,汽车速度的规律是无法用数学公式来描述的。
有@Maxim Dmitrievsky的 说法,非随机过程必须是周期性的,嗯,这不是非随机性的 "必要条件"...指数的同一图形不是周期性的,但也不会是随机的
一个非随机过程可能有一个线性趋势或一个周期性趋势。但仍然必须有一些东西将这个过程定性为非随机的,否则它就是一个具有任何分布密度的SB
如果不能区分恒定成分,那么这个过程当然是随机的,有什么可想的呢?
一个随机的过程可以假装非随机的,是偶然的。这就是为什么在市场上经常有一种错觉,认为它是可以预测的,但随后这个时期过去了,所有的信号都合并了