赫斯特指数 - 页 9 12345678910111213141516...46 新评论 Neutron 2009.02.02 05:48 #81 Prival писал(а)>> 不,不是这样的。根据这个公式,似乎GVH是相关的。所有的时间r都在负0.5左右。 下面是测试代码。 检查了一下。 谢尔盖,让我们一步一步来吧。 1.我们用类似于报价单的BP来工作。这样的系列是通过整合CB与零MO得到的。零MO的CB例子。 dX=rnorm(n+1,0,10),其中n+1是具有高斯分布的CB成员数,0在我的例子中是MO等于0,在你的例子中是10,10在我的例子中是这个分布的宽度,在你的例子中是100。为了构建类似于价格的BP,我们需要对初始序列进行整合(找到它的换算和)。 下面是综合CB的增量的分布情况(左图)和BP背景下的增量本身(右图的红线和蓝线)。 谢尔盖,我们正在研究BP(蓝色的)的属性,而在你的帖子中,你把最开始的差值(在我的符号中是dX,在你的符号中是X)代入公式,计算系列中第一个差值的相关系数。当然,你会得到R=0.5,而且不应该有另一个(它被证明是初级的)。因此,如果你现在用我提出的公式计算MO为零的综合CB(右图中的蓝色)的r,你会得到预期的零。 当然,这与一系列dX增量的r是一样的(但是,通过不同的公式)。 我希望我们现在在这一点上达成了共识? P.S. 你可以这样做。 当然,这并不能改变问题的关键。 Prival 2009.02.02 11:52 #82 好吧,让我们把话说清楚。 我按你说的做了,我用MOJ=0重新整合了CB。这里是所有的代码。 乍看之下似乎还可以。但是有一个陷阱。让我们把一个相关的数组送入公式的输入。作为趋势+噪音。y=a*x+b+rnorm()。这可以通过设置0.5而不是MOJ=0来简单实现。 从图中你可以看到,曲线(蓝色)是明显相关的。在把它分成两个数组A和B之后,让我们计算一下相关系数,结果是0.993。根据你的公式,它是0.225。 问题是,根据定义,相关系数(CC)是在两个数组之间计算的。你用的是同一个人。你可以通过将一个数组 与它自己进行比较来做到这一点。这叫ACF,即形成两个数组A--初始的,第二个B相对于A在时间上移位,并建立一个图形--相关系数对移位的依赖。如果没有转移,ACF当然=1。这里是最后一条蓝色曲线的ACF图。 这就是近似值。因此,我仍然坚持我的观点,即你是按这个公式计算的,但它不是AC。这些数字并不相称。 但我们已经走偏了。我们必须首先正确计算Hurst,然后看看它与QC有什么不同。 [删除] 2009.02.02 11:56 #83 这里有 一篇有趣的论文,分析了不同的时间序列 使用赫斯特指数。 Neutron 2009.02.02 12:27 #84 Prival писал(а)>>图中显示,曲线(蓝色)是明显相关的。把它分成两个数组A和B,我们发现相关系数,是0.993。你的公式给了我们0.225。 在这里,我没有完全理解它。 你把趋势BP分为哪些数组?变成一个直的Y=a*X+b和一个MO为零的随机分量,在它们之间你寻找相关系数? Aleku 写道>> 这里有 一篇有趣的论文,对各种时间序列做了分析 使用赫斯特的索引。 谢谢你。让我们看一看。 Neutron 2009.02.02 12:38 #85 Neutron писал(а)>> 我在这里没有得到所有的权利。 我现在明白了。 您正在寻找原始血压(不是它的增量)和同一血压之间的相关系数,但向右移动500个计数。也就是说,你要找的是两个始终为正的BP之间的相关系数!嗯,当然会是正数,而且总是非常大(约1)。 谢尔盖,我不明白你!你算什么,最初的血压和相同但移位的血压之间的相关系数?我们到底需要它做什么!?我们对初始BP的第一差值系列 中相邻样本之间的 相关系数感兴趣。正是这个系数显示了预期增量对以前增量的依赖性。正是这个系数与Hurst移位1/2后的系数相同。 TheXpert 2009.02.02 13:00 #86 Neutron >> : >> 谢谢你。>> 我们会看到。 这里 似乎有一些真理。 我试图实施它,但我得到了非常接近于1的费率。 ______________ 重读文章 -- 我想我站在了硬币的错误一边。 对于货币对来说,赫斯特指数应该为衍生品计算,我为汇率计算。 Neutron 2009.02.02 13:34 #87 TheXpert писал(а)>>重读文章 -- 有点像踩到了耙子。 是的:-) 领先于自己。 以下是综合SV和EURGBP利率的系列情况(左图),以下是它们在不同TF上的增量幅度,为双对数尺度(右图),在标轴上绘制了TF的对数。 Hers,断言这些线的斜率角的正切值对于随机综合变量来说等于1/2(在这样的商数上进行交易是没有意义的),对于回撤市场来说小于1/2,对于趋势市场来说大于1/2。让我们看看这个角度对东北来说等于什么。在这里,我们可以像文章中建议的那样,画一条ISC线并找到它的斜率,但我将在本地找到这个值--通过画一条穿过每两点的线。其结果是每个TF的PC。 这里的圆圈显示的是CB的PC(红色)和蓝色的欧元GBP商数的标轴上的TF(分钟)。交叉点显示了相邻读数之间的相关系数,为原始系列的第一个差值,偏移量为1/2。相关系数是根据本页面第一条信息中给出的公式计算的。可以看出,这两种估计BP可预测性的方法之间的一致是令人满意的,而我的情况下的公式则小得多(只有一个)。事实上,这也是需要展示的内容。 此外,根据定义,随机数列给出了PX=1/2,r=0(图中有一个偏差)。对于商数来说,一个滚动趋势(反持久性)是清晰可见的,越大越小的TF。 [删除] 2009.02.02 13:49 #88 Neutron >> : 这里我们展示了CB的PCB(红色)和蓝色的EURGBP kotier的标轴,TF是以分钟为单位绘制的。 根据定义,随机数列给出了PX=1/2,r=0(图中有一个偏差)。对于cotier,我们可以清楚地看到一个滚动趋势(反持久性),越大越小的TF。 这可能是为什么小费们如此喜欢欧元英镑的原因。 Neutron 2009.02.02 13:51 #89 Aleku писал(а)>> 我想这就是为什么英国人如此喜欢欧元英镑的原因。 这很明显! [删除] 2009.02.02 13:58 #90 Neutron >> : 这很明显! 出于纯粹的好奇心--我想找到极其持久的配对。 或至少是发生持久性的条件)。 12345678910111213141516...46 新评论 您错过了交易机会: 免费交易应用程序 8,000+信号可供复制 探索金融市场的经济新闻 注册 登录 拉丁字符(不带空格) 密码将被发送至该邮箱 发生错误 使用 Google 登录 您同意网站政策和使用条款 如果您没有帐号,请注册 可以使用cookies登录MQL5.com网站。 请在您的浏览器中启用必要的设置,否则您将无法登录。 忘记您的登录名/密码? 使用 Google 登录
不,不是这样的。根据这个公式,似乎GVH是相关的。所有的时间r都在负0.5左右。
下面是测试代码。
检查了一下。
谢尔盖,让我们一步一步来吧。
1.我们用类似于报价单的BP来工作。这样的系列是通过整合CB与零MO得到的。零MO的CB例子。
dX=rnorm(n+1,0,10),其中n+1是具有高斯分布的CB成员数,0在我的例子中是MO等于0,在你的例子中是10,10在我的例子中是这个分布的宽度,在你的例子中是100。为了构建类似于价格的BP,我们需要对初始序列进行整合(找到它的换算和)。
下面是综合CB的增量的分布情况(左图)和BP背景下的增量本身(右图的红线和蓝线)。
谢尔盖,我们正在研究BP(蓝色的)的属性,而在你的帖子中,你把最开始的差值(在我的符号中是dX,在你的符号中是X)代入公式,计算系列中第一个差值的相关系数。当然,你会得到R=0.5,而且不应该有另一个(它被证明是初级的)。因此,如果你现在用我提出的公式计算MO为零的综合CB(右图中的蓝色)的r,你会得到预期的零。
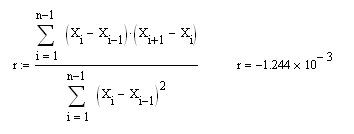
当然,这与一系列dX增量的r是一样的(但是,通过不同的公式)。
我希望我们现在在这一点上达成了共识?
P.S. 你可以这样做。
好吧,让我们把话说清楚。
我按你说的做了,我用MOJ=0重新整合了CB。这里是所有的代码。
乍看之下似乎还可以。但是有一个陷阱。让我们把一个相关的数组送入公式的输入。作为趋势+噪音。y=a*x+b+rnorm()。这可以通过设置0.5而不是MOJ=0来简单实现。
从图中你可以看到,曲线(蓝色)是明显相关的。在把它分成两个数组A和B之后,让我们计算一下相关系数,结果是0.993。根据你的公式,它是0.225。
问题是,根据定义,相关系数(CC)是在两个数组之间计算的。你用的是同一个人。你可以通过将一个数组 与它自己进行比较来做到这一点。这叫ACF,即形成两个数组A--初始的,第二个B相对于A在时间上移位,并建立一个图形--相关系数对移位的依赖。如果没有转移,ACF当然=1。这里是最后一条蓝色曲线的ACF图。
这就是近似值。因此,我仍然坚持我的观点,即你是按这个公式计算的,但它不是AC。这些数字并不相称。
但我们已经走偏了。我们必须首先正确计算Hurst,然后看看它与QC有什么不同。
这里有 一篇有趣的论文,分析了不同的时间序列
使用赫斯特指数。
图中显示,曲线(蓝色)是明显相关的。把它分成两个数组A和B,我们发现相关系数,是0.993。你的公式给了我们0.225。
在这里,我没有完全理解它。
你把趋势BP分为哪些数组?变成一个直的Y=a*X+b和一个MO为零的随机分量,在它们之间你寻找相关系数?
这里有 一篇有趣的论文,对各种时间序列做了分析
使用赫斯特的索引。
我在这里没有得到所有的权利。
我现在明白了。
您正在寻找原始血压(不是它的增量)和同一血压之间的相关系数,但向右移动500个计数。也就是说,你要找的是两个始终为正的BP之间的相关系数!嗯,当然会是正数,而且总是非常大(约1)。
谢尔盖,我不明白你!你算什么,最初的血压和相同但移位的血压之间的相关系数?我们到底需要它做什么!?我们对初始BP的第一差值系列 中相邻样本之间的 相关系数感兴趣。正是这个系数显示了预期增量对以前增量的依赖性。正是这个系数与Hurst移位1/2后的系数相同。
>> 谢谢你。>> 我们会看到。
这里 似乎有一些真理。
我试图实施它,但我得到了非常接近于1的费率。
______________
重读文章 -- 我想我站在了硬币的错误一边。
对于货币对来说,赫斯特指数应该为衍生品计算,我为汇率计算。
重读文章 -- 有点像踩到了耙子。
是的:-)
领先于自己。
以下是综合SV和EURGBP利率的系列情况(左图),以下是它们在不同TF上的增量幅度,为双对数尺度(右图),在标轴上绘制了TF的对数。
Hers,断言这些线的斜率角的正切值对于随机综合变量来说等于1/2(在这样的商数上进行交易是没有意义的),对于回撤市场来说小于1/2,对于趋势市场来说大于1/2。让我们看看这个角度对东北来说等于什么。在这里,我们可以像文章中建议的那样,画一条ISC线并找到它的斜率,但我将在本地找到这个值--通过画一条穿过每两点的线。其结果是每个TF的PC。
这里的圆圈显示的是CB的PC(红色)和蓝色的欧元GBP商数的标轴上的TF(分钟)。交叉点显示了相邻读数之间的相关系数,为原始系列的第一个差值,偏移量为1/2。相关系数是根据本页面第一条信息中给出的公式计算的。可以看出,这两种估计BP可预测性的方法之间的一致是令人满意的,而我的情况下的公式则小得多(只有一个)。事实上,这也是需要展示的内容。
此外,根据定义,随机数列给出了PX=1/2,r=0(图中有一个偏差)。对于商数来说,一个滚动趋势(反持久性)是清晰可见的,越大越小的TF。
这里我们展示了CB的PCB(红色)和蓝色的EURGBP kotier的标轴,TF是以分钟为单位绘制的。
根据定义,随机数列给出了PX=1/2,r=0(图中有一个偏差)。对于cotier,我们可以清楚地看到一个滚动趋势(反持久性),越大越小的TF。
这可能是为什么小费们如此喜欢欧元英镑的原因。
我想这就是为什么英国人如此喜欢欧元英镑的原因。
这很明显!
这很明显!
出于纯粹的好奇心--我想找到极其持久的配对。
或至少是发生持久性的条件)。