在另一个项目 中,我对 20-50 行循环中的快速误差计算和经典误差计算进行了比较:(我假设您在 5 万行时也有同样的累积误差,在数百万行时甚至更多)
. 。
我首先用眼睛比较了 50 行数据。它们没有错误。
但误差被视为累积总和。在每次计算中,我们可能会有 1e-14 ...1e-17 错误。将这些误差多次相加 - 总误差可能超过 1e-5。
我做了更深入的比较。取 50,000 行,然后比较误差,如果差别很大,我就把它们显示在屏幕上。结果如下
有个别累积误差超过 1e-4(即小数点后第 4 位的差异)。
速度当然不错,但如果字符串不是 5 万个,而是 5 亿个呢?恐怕结果绝对无法与循环中的精确计算相提并论。
fast_error= 9.583545e+02 true_error= 9.582576e+02
fast_error= 9.204969e+02 true_error= 9.204000e+02
fast_error= 8.814563e+02 true_error= 8.813594e+02
fast_error= 8.411763e+02 true_error= 8.410794e+02
fast_error= 7.995969e+02 true_error= 7.995000e+02
fast_error= 7.566543e+02 true_error= 7.565574e+02
fast_error= 7.246969e+02 true_error= 7.246000e+02
fast_error= 6.916562e+02 true_error= 6.915593e+02
fast_error= 6.574762e+02 true_error= 6.573793e+02
fast_error= 6.220969e+02 true_error= 6.220000e+02
fast_error= 5.854540e+02 true_error= 5.853571e+02
fast_error= 5.588969e+02 true_error= 5.588000e+02
fast_error= 5.313562e+02 true_error= 5.312593e+02
fast_error= 5.027762e+02 true_error= 5.026792e+02
fast_error= 4.730969e+02 true_error= 4.730000e+02
fast_error= 4.422538e+02 true_error= 4.421569e+02
fast_error= 4.205969e+02 true_error= 4.205000e+02
fast_error= 3.980561e+02 true_error= 3.979592e+02
fast_error= 3.745761e+02 true_error= 3.744792e+02
fast_error= 3.500969e+02 true_error= 3.500000e+02
fast_error= 3.245534e+02 true_error= 3.244565e+02
fast_error= 3.072969e+02 true_error= 3.072000e+02
fast_error= 2.892560e+02 true_error= 2.891591e+02
fast_error= 2.703760e+02 true_error= 2.702791e+02
fast_error= 2.505969e+02 true_error= 2.505000e+02
fast_error= 2.298530e+02 true_error= 2.297561e+02
fast_error= 2.164969e+02 true_error= 2.164000e+02
fast_error= 2.024559e+02 true_error= 2.023590e+02
fast_error= 1.876759e+02 true_error= 1.875789e+02
fast_error= 1.720969e+02 true_error= 1.720000e+02
fast_error= 1.556525e+02 true_error= 1.555556e+02
fast_error= 1.456969e+02 true_error= 1.456000e+02
fast_error= 1.351557e+02 true_error= 1.350588e+02
fast_error= 1.239757e+02 true_error= 1.238788e+02
fast_error= 1.120969e+02 true_error= 1.120000e+02
fast_error= 9.945174e+01 true_error= 9.935484e+01
fast_error= 9.239691e+01 true_error= 9.230000e+01
fast_error= 8.48555553e+01 true_error= 8.475862e+01
fast_error= 7.677548e+01 true_error= 7.667857e+01
fast_error= 6.809691e+01 true_error= 6.800000e+01
fast_error= 5.875075e+01 true_error= 5.865385e+01
fast_error= 5.409691e+01 true_error= 5.400000e+01
fast_error= 4.905524e+01 true_error= 4.895833e+01
fast_error= 4.357517e+01 true_error= 4.347826e+01
fast_error= 3.759691e+01 true_error= 3.750000e+01
fast_error= 3.104929e+01 true_error= 3.095238e+01
fast_error= 2.829691e+01 true_error= 2.820000e+01
fast_error= 2.525480e+01 true_error= 2.515789e+01
fast_error= 2.187468e+01 true_error= 2.177778e+01
fast_error= 1.809691e+01 true_error= 1.800000e+01
fast_error= 1.384691e+01 true_error= 1.375000e+01
fast_error= 1.249691e+01 true_error= 1.240000e+01
fast_error= 1.095405e+01 true_error= 1.085714e+01
fast_error= 9.173829e+00 true_error= 9.076923e+00
fast_error= 7.096906e+00 true_error= 7.000000e+00
fast_error= 4.642360e+00 true_error= 4.545455e+00
fast_error= 4.196906e+00 true_error= 4.100000e+00
fast_error= 3.652461e+00 true_error= 3.555556e+00
fast_error= 2.971906e+00 true_error= 2.875000e+00
fast_error= 2.096906e+00 true_error= 2.0000000000e+00
fast_error= 9.302390e-01 true_error= 8.33333333e-01
fast_error= 8.96909057e-01 true_error= 8.000000e-01
fast_error= 8.469057e-01 true_error= 7.500000e-01
fast_error= 7.635724e-01 true_error= 6.666667e-01
fast_error= 5.969057e-01 true_error= 5.000000e-01
fast_error= 4.546077e+00 true_error= 4.545455e+00
fast_error= 4.100623e+00 true_error= 4.100000e+00
fast_error= 3.556178e+00 true_error= 3.555556e+00
fast_error= 2.875623e+00 true_error= 2.875000e+00
fast_error= 2.000623e+00 true_error= 2.000000e+00
fast_error= 8.339561e-01 true_error= 8.333333e-01
fast_error= 8.006228e-01 true_error= 8.000000e-01
fast_error= 7.506228e-01 true_error= 7.500000e-01
fast_error= 6.672894e-01 true_error= 6.666667e-01
fast_error= 5.006228e-01 true_error= 5.000000e-01
问题出在哪里?
在训练过程中,终端会崩溃,并不总是出错,就像有什么鬼怪一样。
N 0 22:58:20.933 Core 1 2021.02.01 00:00:00 program string is NULL or empty
MP 0 22:58:20.933 Core 1 2021.02.01 00:00:00 OpenCL program create failed.Error code=4003
CD 0 22:58:20.933 Core 1 2021.02.01 00:00:00 OnInit - 153 -> Error of reading EURUSD_PERIOD_H1_ 20AttentionMLMH_d.nnw prev Net 5015
RD 0 22:58:20.933 Core 1 2021.02.01 00:00:00 program string is NULL or empty
QN 0 22:58:20.933 Core 1 2021.02.01 00:00:00 OpenCL program create failed.Error code=4003
IO 0 22:58:20.933 Core 1 final balance 10000.00 USD
LE 2 22:58:20.933 Core 1 2021.02.19 23:54:59 invalidpointer access in 'NeuroNet.mqh' (2271,16)
MS 2 22:58:20.933 Core 1 OnDeinit critical error
NG 0 22:58:20.933 Core 1 EURUSD,H1: 863757 ticks, 360 bars generated.环境在 0:00:00.018 同步。测试在 0:00:00.256 时通过。
QD 0 22:58:20.933 Core 1 EURUSD,H1:从登录到停止测试的总时间为 0:00:00.274(包括 0:00:00.018 的历史数据同步)
LQ 0 22:58:20.933 Core 1 使用了 321 Mb 内存,包括 0.47 Mb 歷史數據,64 Mb 勾選數據
JF 0 22:58:20.933 Core 1 log file "C:\Users\Buruy\AppData\Roaming\MetaQuotes\Tester\36A64B8C79A6163D85E6173B54096685\Agent-127.0.0.0.1-3000logs\20210410.log" written
PP 0 22:58:20.939 Core 1 connection closed
提前感谢您的帮助!..!
德米特里 你好!几个月来,我观察到 OOS 运行和最终工作之间存在很大差异,而且时间间隔相同,但已经是 Expert Advisor 了。所有信号都是统一的(我将每条所有信号卸载到一个文件中并进行比较),网络设置自然也是相同的。我怀疑保存和读取训练的过程没有正常工作。在 NeuroNet.mph 文件中,每个网络都配置了单独的训练保存方式
bool CNeuronProof::Save(const int file_handle)
bool CNeuronBase::Save(int file_handle)
bool CNeuronConv::Save(const int file_handle)
bool CNeuronLSTM::Save(const int file_handle)
bool CNeuronBaseOCL::Save(const int file_handle)
bool CNeuronAttentionOCL::Save(const int file_handle)
等等。
并使用保存
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true)
请解释其中的区别,是否有可能在一个纪元后将保存的数据与内存中的训练数据相匹配?
训练时的输出信号数据 TempData 和输出神经元 ResultData
和测试时的输出神经元 ResultData。我在 WinMerge 程序中比较了这两个文件。
德米特里 你好!几个月来,我观察到 OOS 运行和最终工作之间存在很大差异,而且时间间隔相同,但已经是 Expert Advisor 了。所有信号都是统一的(我将每条所有信号卸载到一个文件中并进行比较),网络设置自然也是相同的。我怀疑保存和读取训练的过程没有正常工作。在 NeuroNet.mph 文件中,每个网络都配置了单独的训练保存方式
bool CNeuronProof::Save(const int file_handle)
bool CNeuronBase::Save(int file_handle)
bool CNeuronConv::Save(const int file_handle)
bool CNeuronLSTM::Save(const int file_handle)
bool CNeuronBaseOCL::Save(const int file_handle)
bool CNeuronAttentionOCL::Save(const int file_handle)
等等。
并使用保存
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true)
请解释其中的区别,是否有可能在一个纪元后将保存的数据与内存中的训练数据相匹配?
训练时的输出信号数据 TempData 和输出神经元 ResultData
和测试时的输出神经元 ResultData。我在 WinMerge 程序中比较了这两个文件。
日安,德米特里。
让我们看看 CNet::Save(...) 方法。记录网络训练 状态变量后,神经层数组(CArrayLayer 继承自 CArrayObj)的保存方法被调用
bool CNet::Save(string file_name,double error,double undefine,double forecast,datetime time,bool common=true) { if(MQLInfoInteger(MQL_OPTIMIZATION) || MQLInfoInteger(MQL_TESTER) || MQLInfoInteger(MQL_FORWARD) || MQLInfoInteger(MQL_OPTIMIZATION)) return true; if(file_name==NULL) return false; //--- int handle=FileOpen(file_name,(common ? FILE_COMMON : 0)|FILE_BIN|FILE_WRITE); if(handle==INVALID_HANDLE) return false; //--- if(FileWriteDouble(handle,error)<=0 || FileWriteDouble(handle,undefine)<=0 || FileWriteDouble(handle,forecast)<=0 || FileWriteLong(handle,(long)time)<=0) { FileClose(handle); return false; } bool result=layers.Save(handle); FileFlush(handle); FileClose(handle); //--- return result; }
CArrayLayer 类没有 Save 方法,因此需要调用父类 CArrayObj::Save(const int file_handle)。该方法的主体包含一个循环,用于枚举所有嵌套对象,并调用每个对象的 Save 方法。
//+------------------------------------------------------------------+ //| 将数组写入文件| //+------------------------------------------------------------------+ bool CArrayObj::Save(const int file_handle) { int i=0; //--- 检查 if(!CArray::Save(file_handle)) return(false); //--- 写入数组长度 if(FileWriteInteger(file_handle,m_data_total,INT_VALUE)!=INT_VALUE) return(false); //--- 写入数组 for(i=0;i<m_data_total;i++) if(m_data[i].Save(file_handle)!=true) break; //--- 结果 return(i==m_data_total); }
换句话说,这里使用了嵌套玩偶的原理:我们调用顶层对象的 Save 方法,然后在该方法内部搜索所有嵌套对象,并为每个对象调用同名方法。
从文件中加载数据的组织方式与此类似。
关于训练和运行过程中的不同评估。我不知道你的神经网络在运行模式下是如何组织的,但在训练模式下,神经网络的参数是不断变化的。因此,相同的输入数据会产生不同的结果。
Dmitry。
附注:您可以通过制作一个小型测试程序来检查保存和读取数据的正确性,在该程序中,您可以从一个文件中读取神经网络,并立即将其保存到一个新文件中。然后比较这两个文件。如果发现任何差异,请写信给我,我会进行检查。
下午好,德米特里。
让我们来看看 CNet::Save(...) 方法。记录网络训练 状态变量后,神经层数组(CArrayLayer 继承自 CArrayObj)的 Save 方法被调用
CArrayLayer 类没有 Save 方法,因此需要调用父类 CArrayObj::Save(const int file_handle)。该方法的主体包含一个循环,用于枚举所有嵌套对象,并调用每个对象的 Save 方法。
换句话说,这里使用了嵌套玩偶的原理:我们调用顶层对象的 Save 方法,然后在该方法内部搜索所有嵌套对象,并为每个对象调用同名方法。
从文件加载数据的组织方式与此类似。
关于训练和运行过程中的不同评估。我不知道你的神经网络在运行模式下是如何组织的,但在训练模式下,神经网络的参数是不断变化的。因此,相同的输入数据会产生不同的结果。
Dmitry。
附注:您可以通过制作一个小型测试程序来检查保存和读取数据的正确性,在该程序中,您可以从一个文件中读取神经网络,并立即将其保存到一个新文件中。然后比较这两个文件。如果发现任何差异,请写信给我,我会进行检查。
接受,我将尝试用以下方法进行检查。在第一个条形图中,我会将 TempData(信号)和 OUTPUT 神经元保存到文件中。首先不加载文件,但进行训练,然后从相同的第一个条形图加载训练,但过程中不进行训练。我将回信。
p/s/ 因为在训练过程中,每个条形图都会真正学习神经元卡,在测试过程中,测试人员执行了相同的过程,但减去了 N 个条形图。但我同意应该是这样。
亲爱的德米特里
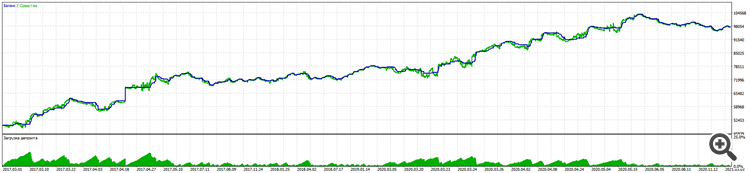
在长期的工作过程中,我在您的资料库的帮助下,成功地创建了一个交易顾问,在 5 年的欧元兑美元(EURUSD)交易中,取得了从 11% 的缩水到几乎 100% 的收益的好成绩。
Alpari:
在真实账户上的测试也遵循同样的逻辑。
值得注意的是,即使在 BKS 期货上,相同的输入条件下,RURUSD 的结果甚至更好。(我还没有测试其他货币对)。
胜利的关键在于测试了盲目交易(只对过去的时期进行培训)和强制止损,没有马丁格尔和其他技巧,只是有权根据信号在任何方向开立几笔交易。
当然,我必须从 WSE 和斯坦福大学的五周课程以及大量有关神经网络的文章中学习和补充很多东西,尤其是在理解教什么、教什么以及如何教方面。
非常感谢!
请不要停止,继续发展图书馆。
我想请您思考的是
1.还是关于培训的保存问题。我已经写过了,这行不通。您每次都必须学习,而且 "一开始 "就必须学习,不能中断交易。这不是问题,培训很快,但还有第二个问题。
2.一开始,您设置了随机化逻辑来创建主神经元。这会导致多达三个版本的训练。(我认为关键在于主神经元最初是正还是负)。
是的,这也是可以解决的,可以这么说,如果你没有达到正确的指标,就必须从头开始重新训练。
但我相信,你可以从每个神经元的条件权重为 0.01 开始。(不幸的是,过度训练会变得更加明显)。
或者还是学习保留最好的教育副本,那么就是第 1 点。
亲爱的迪米特里
在长期的工作过程中,我在您的资料库的帮助下,成功地创建了一个交易顾问,5 年欧元兑美元的收益率从 11% 下降到近 100%,取得了很好的效果。
Alpari:
在真实账户上的测试也遵循同样的逻辑。
值得注意的是,即使在 BKS 期货上,相同的输入条件下,RURUSD 的结果也更好。(我还没有在其他货币对上进行测试)。
胜利的关键在于测试了盲目交易(只对过去的时期进行培训)和强制止损,没有马丁格尔和其他技巧,只是有权根据信号在任何方向开立几笔交易。
当然,我还得从 WSE 和斯坦福大学的五周课程以及大量有关神经网络的文章中学习和补充很多东西,尤其是在理解教什么、教什么以及如何教方面。
非常感谢!
请不要停止,继续发展图书馆。
我想请你们考虑一下
1.仍在保留培训。正如我已经写过的,这行不通。你必须每次都学习,而且 "一开始就学",不能中断交易。这不是问题,培训很快,但还有第二个问题。
2.一开始,您设置了随机化逻辑来创建主神经元。这会导致多达三个版本的训练。(我认为关键在于主神经元最初是正还是负)。
是的,你也可以与之抗衡,可以这么说,如果你没有达到所需的指标,可以从头开始强制重新训练。
但我相信,你可以从每个神经元的条件权重为 0.01 开始。(不幸的是,过度训练会变得更加明显)
或者还是学习保留最好的教育副本,那么就是第 1 点。
感谢迪米特里的赞誉。以一个恒定值启动所有权重的做法是不好的。在这种情况下,学习过程中所有神经元都会同步工作。整个神经网络会退化为每一层上的一个神经元。
....
我想请大家思考的是
1.仍然保留培训。正如我已经写过的,这行不通。 你必须每次都学习,而且 "一开始 "就学习,不能中断交易。这不是问题,培训很快,但还有第二个问题。
2.一开始,您设置了随机化逻辑来创建主神经元。这会导致多达三个版本的训练。(我认为关键在于主神经元最初是正还是负)。
是的,你也可以与之对抗,可以这么说,如果你没有达到所需的指标,就强制从头开始重新训练。
但我相信,你可以从每个神经元的条件权重为 0.01 开始。(不幸的是,过度训练会变得更加明显)
或者仍然学习保留最好的教育副本,那么就是第 1 点。
迪米特里,我按照作者的建议进行了测试。
1.训练多个历元,每个历元后保存网络文件。
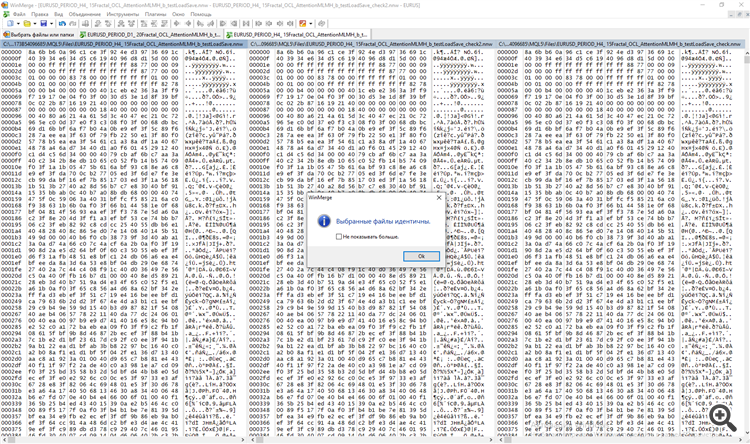
2.从图表中删除。再次运行并启用参数 testSaveLoad - 在读取之前训练的网络后,Expert Advisor 会再次写入网络,重复读写循环并卸载,除了带有 _check 和 _check2 前缀的原始网络外,我们还会得到三个文件。
3.我们将这三个文件进行比较,以便 a) 通过测试学习编程 b) 查找自身错误。
谢谢阿列克谢,我没有在这里公布结果。
问题出在其他地方。
保存/加载过程正常。
解决方案是在使用 "随机化 "创建神经元网络元素的一行中找到的。
bool CArrayCon::CreateElement(int index) { if(index<0 || index>=m_data_max) return false; //--- xor128; double weigh=(double)rnd_w/UINT_MAX-0.5; m_data[index]=new CConnection(weigh); if(!CheckPointer(m_data[index])!=POINTER_INVALID) return false; //--- return (true); }
我用一个更稳定的创建神经元函数替换了它,重要的是要创建相同数量的正负神经元,这样网络就不会倾向于销售或购买。
double weigh=(double)MathMod(index,0)?sin(index):sin(-index);
为了以防万一,我对创建初始权重的函数也做了同样的处理。
double CNeuronBaseOCL::GenerateWeight(void) { xor128; double result=(double)rnd_w/UINT_MAX-0.5; //--- return result; } //+----
现在,在加载训练文件后测试训练好的网络 时,回溯测试给出了相同的结果。
输入为每秒统一。
新文章 神经网络变得轻松(第十三部分):批次常规化已发布:
在上一篇文章中,我们开始研究旨在提高神经网络训练品质的方法。 在本文中,我们将继续这个主题,并会研讨另一种方法 — 批次数据常规化。
在神经网络应用实践中运用了多种数据常规化方法。 然而,它们的作用均是为了令训练样本数据和神经网络隐藏层的输出保持在一定范围内,并具有某些样本统计特征,如方差和中位数。 这一点很重要,因为网络神经元在训练过程中利用线性变换将样本朝逆梯度偏移。
参考一个含有两个隐藏层的全连接感知器。 在前馈验算过程中,每一层都会生成一个特定的数据集,作为下一层的训练样本。 输出层的结果与参考数据进行比较。 然后,在反馈验算过程中,误差梯度自输出层穿过隐藏层朝向初始数据传播。 每个神经元接收到误差梯度后,我们更新权重系数,为最后一次前馈验算的训练样本调整神经网络。 此处会产生一个冲突:第二个隐藏层(下图中的 H2)会基于第一个隐藏层(图中的 H1)输出的数据样本进行调整,而通过改变第一个隐藏层的参数,我们已更改了数据数组。 换言之,我们调整第二个隐藏层,其数据样本不再存在。 类似的状况也发生在输出层,因第二个隐藏层输出业已变化,故它也会被调整。 如果我们参考第一和第二隐藏层之间的失真,误差尺度会更大。 神经网络越深,影响越强。 这种现象被称为内部协变量偏移。
经典神经网络通过降低学习率部分解决了这个问题。 权重的微小变化不会导致神经层输出的样本分布发生显著变化。 但这种方式并未解决随着神经网络层数增加而出现的问题放大,且还降低了学习速度。 减小学习率的另一个问题是该过程可能会卡在局部最小值上,我们曾在第六篇文章里讨论过。
作者:Dmitriy Gizlyk