文章 "创建非滞后数字滤波器"

[MetaQuotes]

新文章 创建非滞后数字滤波器已发布：

本文介绍在流数据中确定有效信号（趋势）的一种方法。应用至市场报价的小滤波（平滑）测试表明创建未在最后的柱上重绘的非滞后数字滤波器（指标）的潜力。

群集滤波器

群集滤波器是接近初始序列的一组数字滤波器。不要将群集滤波器与群集指标混淆。

群集滤波器在实时分析非稳态时间序列 - 换言之，流数据 - 时十分方便。这意味着，这些滤波器的主要任务是实时获得接收到的新数据的最有可能的平滑值，而非平滑已知时间序列值。

与各种分解方法或所需频率的滤波器不同的是，群集滤波器创建初始序列的可能值的一个组合或一个范围，然后进一步分析以接近初始序列。输入序列在分析中更像是一个参考而不是目标。主分析涉及在处理接收到的数据后由一组滤波器计算得到的值。

图 1. 简单群集滤波器图解

一般情况下，群集中包含的每个滤波器有其各自的特性，并且不以任何方式相关。这些滤波器有时候定制用于分析它们自己的平稳时间序列，这描述了初始非 平稳时间序列的个体属性。在最简单的情况下，如果初始非稳态序列改变其参数，滤波器则“切换”。因此，群集滤波器在本质上追踪实时更改。

作者：Konstantin Gruzdev

[Sergey Pavlov]

感谢作者提供了一篇有趣的文章。

[Mikhael Isakov]

在过去的几年里，我一直在考虑建立一个无滞后过滤器。我也经常得到一些似乎比其他方法更好的结果，甚至是非滞后的结果。所有这些都在步骤分析中被打破了。我要求作者将输入模型信号变为一个 Heaviside 函数：一个阶跃，直到 T 级 =0 的时刻，之后是一个阶跃。并在此基础上显示滤波线。我有 99.99% 的把握，我们会看到一条曲线在某个时间间隔内到达 1 级，即滞后。一个理想的、真正的、非滞后的滤波器应该能够处理 "阶跃"，使输出等于输入。否则，"无滞后 "的推理就是修修补补。尽管我支持作者的观点：创建一个无滞后、无绘制的滤波器是可能的。

附注：与其他滤波器的比较应在一个 "台阶 "上进行，将所有滤波器放在一张图上。

附注：如果这已经在某个视频中实现了，请原谅我现在（在工作电脑上）看不到视频（显然是在 youtube 上发布的？）

[Konstantin Gruzdev]

我将为带过滤器的动量添加一个测试步骤。

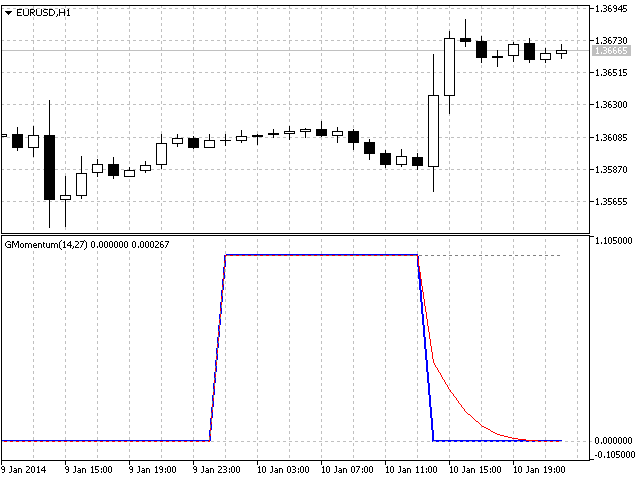
在第四段视频中，我们可以清楚地看到过滤器对报价流程中步骤的反应。

[Mikhael Isakov]

Lizar:

我将为带过滤器的动量添加一个测试步骤。

在第四段视频中，我们可以清楚地看到过滤器对报价流中的阶跃有何反应。

比方说，在某种有效的（不是字面意义上的）平均意义上，周期为 101 条，因此滞后期为 50 条。我可以很清楚地看到这一点。但在报价上，两个水平部分（0 和 1 条件）加在一起只有 20 个条形图，而在报价周围，我看不到任何类似的东西。

应该只输入模型信号来研究滤波器，然后在了解其性质后，再欣赏报价工作图片。

[Konstantin Gruzdev]

MAIS:

比方说，在某种有效的（不是字面意义上的）平均意义上，周期是 101 个小节，因此滞后期是 50 个小节。在干净的台阶上，我可以很清楚地看到这一点。但在报价上，两个水平部分（0 和 1 条件）加起来只有 20 个条形图，而在报价周围，我看不到类似的东西。

应该只输入模型信号来研究滤波器，然后在了解其性质后，再欣赏报价工作图片。

我明白，我会添加这样的测试。

[Mikhael Isakov]

Lizar:
我知道了，我会添加这样一个测试。

谢谢。我在猜测我们会看到什么。也许您的滤镜会比竞争对手显示出更少的延迟和更好的平滑效果。但它百分之百不会是一个无滞后、无绘制的过滤器。下一个问题是--你的滤镜是否足够接近无延迟、无绘制滤镜，从而可以胜任这一角色？在我看来，测试很简单。如果过滤器真的没有滞后，也没有重新绘制，那么我们就可以合理地假设，一个简单的交易策略就会有利可图：如果过滤器高于价格，则买入，反之则卖出。我们将通过在每个条形图中（或当背离超过某个阈值时）进入，并以相同的手数和相等的 TP=SL 进入来实施。例如，TP=SL=50 点。 关键是，如果我们随机进入，在不考虑点差的情况下，我们有 50%的概率抓住 SL。考虑到点差 - 则更多。这就是我们慢慢亏损的原因。如果过滤器没有真正滞后，那么捕捉 TP 的概率会更高（不考虑价差）。如果有影响，我们在分析了相当长的一段报价后不可能没有注意到。如果您能证明在这样一个简单的策略中，在不考虑价差的情况下，TP 的概率至少是 55%，这就足以补偿价差，甚至还能赚到钱。如果您的过滤器真的是非滞后的，那么通过选择过滤器与价格之间差额的阈值，当模块达到阈值时，您就能显示在价差为 70%、80%或 90%以上时的 TP 概率....。如果是 - 您的过滤器几乎不延迟、不拖拉，您的交易策略就是圣杯。如果不是--TP 的概率不超过 SMA 的概率--对不起。

[Konstantin Gruzdev]

MAIS:
谢谢我在猜测我们会看到什么。也许您的滤镜会比竞争对手显示出更少的滞后和更好的平滑效果。但它 100% 不会是一个无滞后、无拉伸的过滤器....。

让我们等待 GMomentum_test 指标的发布，而不是靠猜测得出结论。该指标本应与文章一起发布，但显然他们没有时间准备。现在看来要等到下周一了。

至于一般测试，线性滤波器 的测试并不适用于群集滤波器。更确切地说，它们是可以做的，但不具有指示性，因为聚类滤波器是非线性的。文章中单脉冲的情况就是一个例子。最有可能的是，使用单步函数进行的测试结果也会同样惊人。但是，就像单脉冲一样，这只是一个有趣的平滑特例。仅此而已。

[Mikhael Isakov]

Lizar:

让我们等待 GMomentum_test 指标的公布，这样我们就可以得出结论，而不是靠猜测。该指标本应与文章一起发布，但显然他们没有时间准备。现在看来，它将在周一发布。

至于一般测试，线性滤波器 的测试并不适用于群集滤波器。更确切地说，它们是可以做的，但不具有指示性，因为聚类滤波器是非线性的。文章中单脉冲的情况就是一个例子。最有可能的是，使用单步函数进行的测试结果也会同样惊人。但是，就像单脉冲一样，这只是一个有趣的平滑特例。仅此而已。

这与滤波器测试无关。很明显，非延迟非拉伸滤波器（如果存在的话）是非线性的。这是在测试我提出的几何图形中的交易系统，这个非延迟非拉伸滤波器先验地是有利可图的，而这个理想滤波器的某个近似值也可能是有利可图的。带阶跃的测试并非特例，而是展示滤波器的内在、先天特性，这些特性在任何数据中都会存在，只是在阶跃时才会显现出来。

[Konstantin Gruzdev]

MAIS:

这就是我的收获：

灰色虚线 是海维塞德（Heaviside），蓝色粗线 是动量（Momentum），红色线是打开滤波器后的动量（Momentum）。

[Mikhael Isakov]

Lizar:

这就是我的收获：

灰色虚线 是 Heaviside，蓝色粗线 是动量，红色线 是打开滤波器后的动量。

灰色虚线不是 Heaviside。阶跃应该是垂直的。如果这是因为离散化是在腹轴上进行的，而它是用一条线画出来的，那就太遗憾了。我的意思是要看更高的平滑值。这样，滞后值就会大于显示的 3 个条形图。一般来说，如果滞后很小，我通常会根据需要多次重复练习：我将滤波器应用到滤波结果中，经过一千次重复后，一切都清晰可见，滞后条形图的哪一部分包含在明显的微小平滑算法中也就一目了然了。