你从哪里找到 1/s^2 的维度的?这个比值没有维度。我并没有把它塞进去,我只是假设,作用于某一过程的力的变化率(减小率)与力本身成正比,这并不违背逻辑,然后,这一假设得到了充分证实。作为比例系数,并引入了比率 a (alpha) = 1/tau,它具有时间的倒数维度。通过 a (α) 我可以理解为系统的阻抗,即系统对过程流的阻力,而 tau 则是拉普拉斯变换中时间的图像,正如后来所证明的那样,它允许将过程分析从微分域转到普通域。这意味着任何过程都有自己的时间,与我们的时间不同,而 tau 则充当时间的 "翻译者",如果我可以这样说的话。我在文章中给出了一种估算 tau 的方法:
现在,如果已知函数 f 在时间 t 的相应时刻的值,那么就可以根据该方程确定参数 n、τ 和系数 β 如下:
(12)
(13)
(14)
其中:
函数 f 在时间 t 和时间 t 的相应时刻的值由市场价格 P0,P1,...,Pk 在时间 h0,h1,...,һk 的实际值决定,从其开始不稳定时起,通过数值微分,指区间中间的时刻:
通过私信联系,了解相关条件。
Добрый день, уважаемый Юсуфходжа, подскажите, где можно скачать индикаторы и советники о которых вы говорите?
这些指标是付费的还是什么? 已发布在代码库中,请尽情使用!
发表新文章《市场价格预测的通用回归模型》:
作者:ЮсуфходжаЮсуфходжа
好文章。
令人印象深刻
遗憾的是,文章一开始就出现了错误。
首先,某个时间 t 的价格增量当然会有某个值,我们用 D0 表示它。让我们假设一下。
接下来...现在,在 t=0 时,我知道价格不会受到任何影响,而且外部影响显然也不会带来价格增量。不过,我们还是把三角洲称为 D0。
为什么要这样做呢?毕竟,我们还没有定义这种撞击是什么......
总的来说
遗憾的是,文章一开始就出现了错误。
首先,某个时间 t 的价格增量当然会有某个值,我们用 D0 表示它。让我们假设一下。
接下来...现在,在 t=0 时,我知道价格不会受到任何影响,而且外部影响显然也不会带来价格增量。不过,我们还是把三角洲称为 D0。
为什么要这样做呢?毕竟,我们还没有定义这种撞击是什么......
总的来说...
1. Do 不是价格增量,而是在 t=0 时影响价格的力的初始势能。
2. 从文章中可以看出:"....,假定处于平衡状态的市场价格只能在某种外力 D(t) 的作用下发生变化,外力 D(t) 的大小和数值我们将在与价格相同的维度上进行度量。
我们还可以假定,市场价格 P(t) 随着时间 t 的推移,从这一外力开始影响时起,按某种我们还不知道的规律性从零值不断增加,最终趋于达到无穷大的 P(∞) = D0 值。也就是说,我们所说的 D0 是指市场价格的有限增量或减量,这取决于这种影响力量的性质和符号。
此外,我们假设 D(t=0) = D0。我们进一步假设,在 dt 的无限小时间段内,影响力将以 dD(t) 的值减少,与时间 t 时刻的剩余影响力 D(t) 成比例:
因此,我们可以得到 D(t) 与时间 t 的指数关系式:
其中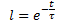
t - 从失稳力影响开始的时间,以时间序列为单位,秒(分、小时、天、周、旬、月、年);
τ(tau)--比例系数,数值上等于过程的时间常数,秒(分、小时、天、星期、几十年、月、年)"。
你从哪里找到 1/s^2 的维度的?这个比值没有维度。我并没有把它塞进去,我只是假设,作用于某一过程的力的变化率(减小率)与力本身成正比,这并不违背逻辑,然后,这一假设得到了充分证实。作为比例系数,并引入了比率 a (alpha) = 1/tau,它具有时间的倒数维度。通过 a (α) 我可以理解为系统的阻抗,即系统对过程流的阻力,而 tau 则是拉普拉斯变换中时间的图像,正如后来所证明的那样,它允许将过程分析从微分域转到普通域。这意味着任何过程都有自己的时间,与我们的时间不同,而 tau 则充当时间的 "翻译者",如果我可以这样说的话。我在文章中给出了一种估算 tau 的方法:
现在,如果已知函数 f 在时间 t 的相应时刻的值,那么就可以根据该方程确定参数 n、τ 和系数 β 如下:
其中:
函数 f 在时间 t 和时间 t 的相应时刻的值由市场价格 P0,P1,...,Pk 在时间 h0,h1,...,һk 的实际值决定,从其开始不稳定时起,通过数值微分,指区间中间的时刻:
f1 = (P1 - P0)/( ch1 - ch0); f2 = (P2 - P1)/( ch2- ch1); f3 = (P3 - P2)/( ch3- ch2); 等等;
t1 = (ch0 + ch1)/2; t2 = (ch1 + ch2)/2; t3 = (ch3 + ch2)/2; 依此类推。