文章 "使用计量经济学方法分析图表"

新评论
 

新文章 使用计量经济学方法分析图表已发布：

本文介绍了用于分析、自相关分析尤其是条件方差分析的计量经济学方法。本文介绍的方法有何益处？使用非线性 GARCH 模型可以从数学角度正式表示分析序列并为指定步骤数建立预测。

Kurtosis of various distributions.

作者：Dennis Kirichenko

 
岛度小于正态分布的分布有一个«толстые хвосты»

这从根本上是错误的。

首先，让我们用俄语来称呼 "峰度 "和 "岛度"，用公认的术语--峰度系数或简称峰度。

其次，"岛度 "和 "肥尾 "在一般情况下没有任何关系。这里有一个反例--拉普拉斯分布（双边指数分布），应该说绝大多数金融时间序列的图形都符合这个分布。它的过度等于 3（即它的顶端比正态分布的顶端更尖锐），但尾部很粗--它们根据 exp(-x) 规律减小，即比高斯分布的 exp(-x^2) 规律更慢。

[删除]  
alsu:

这从根本上说是错误的。

首先，让我们用俄语来称呼 "峰度 "和 "岛度"，使用公认的术语--峰度系数或简称峰度。

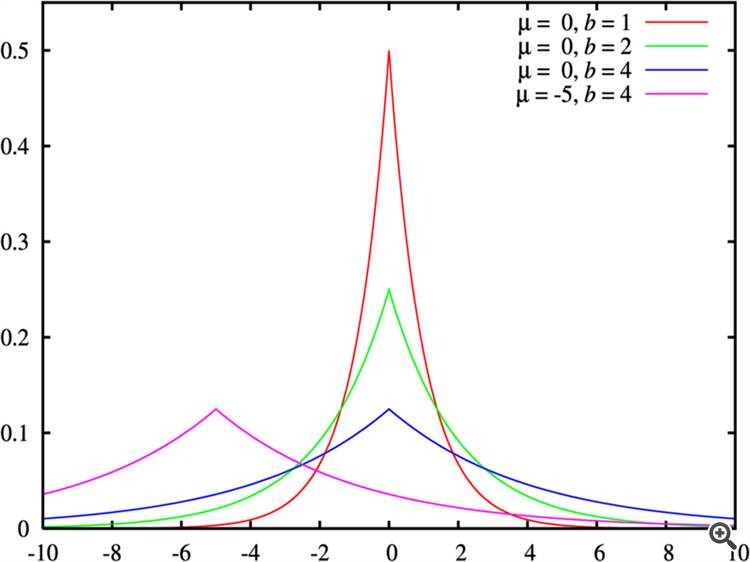
其次，"岛度 "和 "肥尾 "在一般情况下没有任何关系。这里有一个反例--拉普拉斯分布（双边指数分布），应该说绝大多数金融时间序列的图形都符合这个分布。它的过度等于 3（即顶端比正态分布更尖锐），但尾部却很粗--它们根据 exp(-x) 规律减小，即比高斯分布的 exp(-x^2) 慢。

此外，正态分布本身并没有 "过剩 "的概念，只有 "过剩率 "的概念，它是对另一个概念 "分布过剩 "的度量，而这个概念只针对单模态分布。因此，为了正确使用该系数，首先必须确定经验分布函数，这从数学的角度来看并不是一件小事；其次，在一些概率标准的框架内，检查并接受分布具有单一模式的假设，这对于金融序列来说并不总是满足，也是一项非同小可的任务。如果没有这些步骤，就不可能进行进一步的计算，如果需要 "超额系数 "的话。


附注


如果测试表明序列不适用于假定模型，该怎么办？

也没有说明为什么要使用所谓的 "收益率 "系列而不是其他系列，依据是什么。

在实践中，使用资产收益率比直接使用资产价格更可取的主要原因是，收益率具有更具 吸引力的统计特性。

哪些具有吸引力，如何具有吸引力，目的是什么？为什么是有吸引力的而不是权宜之计？选择变换类型的有效数学标准是什么？
 
各位同事，非常感谢你们对这篇文章的关注。如果可能，我会尽量回答所有问题和批评。就我而言，如果您对该主题感兴趣，请阅读文章末尾列出的文献。许多问题会自行消失。
 

alsu:

......我们还是说俄语吧，用公认的术语--超额系数或超额....--来称呼 "峰度 "和 "岛度"。

我特别喜欢alsu 认为 "系数 "和 "过度 "是俄语的这一事实...

 

alsu:

其次，"孤岛性 "和 "肥尾 "一般没有关系。这里有一个反例--拉普拉斯分布（双边指数分布），需要指出的是，绝大多数金融时间序列的图形都符合该分布。它的过度等于 3（即顶部比正态分布更尖锐），但尾部却很粗--根据 exp(-x) 规律减小，即比高斯分布的 exp(-x^2) 慢。

这正是我认为的一般相关性。

图 "不同参数的拉普拉斯分布"中显示了一个 "峰度较小-尾部较厚 "的例子 。


 

我只想在我的文章中补充以下一句："一系列收益的分布比正态分布更经常 表现出肥尾行为"。在英文文献中，"肥尾 "现象被称为过度峰度（excess kurtosis）。具有这种尾部分布的序列被称为leptokurtic，其峰度为正（超过正态分布的峰度）。

然后是峰度系数：

正态分布的 峰度为零，即 γ2 = 0。

如果分布的尾部比正态分布 "轻"，峰度比正态分布尖锐，则γ2 > 0。

如果分布的尾部比正态分布 "重"，峰值比正态分布更 "扁平"，则γ2 < 0。

 
denkir:

我只会在我的文章中添加这样的建议：

加进去。我们将重新发表。
[删除]  
denkir:

我只想在我的文章中补充以下一句："一系列回报的分布比正态分布更经常 表现出肥尾行为"。在英文文献中，"肥尾 "现象被称为过度峰度（excess kurtosis）。具有这种尾部分布的序列被称为leptokurtic，其峰度为正（超过正态分布的峰度）。

然后是峰度系数：

正态分布的 峰度为零，即 γ2 = 0。

如果分布的尾部比正态分布 "轻"，峰度比正态分布尖锐，则γ2 > 0。

如果分布的尾部比正态分布 "重"，峰值比正态分布更 "扁平"，则γ2 < 0。

错误，维基有错误。以均匀分布为例。它的过度可以计算出来，而且根本没有尾部。因此，你被正确地告知，在一般情况下，重力、长度、尾部的存在与峰度系数之间没有关系。三角形分布也是如此。
 

在你们争论术语的时候，我已经利用这篇文章中的观点在一夜之间建立了一些盈利的 EA。:-)

然而，它们的利润非常小，尽管它们相当稳定（根据 12 年的历史记录查看，图表增长得非常漂亮）。文章中描述的方法检测到的相关性相当弱（ 序列的自相关系数 约为 0.01，在特殊情况下接近 0.1，这取决于哪些价格衍生品具有相关性），而且在交易时，它们的利润被价差严重打败。我不得不添加一个过滤器，只在出现强烈信号时才进行交易，否则盈利率曲线就会近似直线下降。

无论如何，还是要感谢作者。这些想法很有价值。我认为，批评者不应该把作者的鼻子戳进数理的深渊，而应该把这篇文章看作是实际实验的一个广阔领域。

[删除]  
ds2:

在你们争论术语的时候，我已经利用这篇文章中的观点在一夜之间建立了一些盈利的 EA。:-)

然而，它们的利润非常小，尽管它们相当稳定（根据 12 年的历史记录查看，图表增长得非常漂亮）。文章中描述的方法检测到的相关性相当弱（序列的自相关系数约为 0.01，在特殊情况下接近 0.1，这取决于哪些价格衍生品具有相关性），而且在交易时，它们的利润被价差严重打败。我不得不添加一个过滤器，只在出现强烈信号时才进行交易，否则盈利率曲线就会近似直线下降。

无论如何，还是要感谢作者。这些想法很有价值。我认为，批评者不应该把作者的鼻子戳进数理的深渊，而应该把这篇文章看作是实际实验的广阔领域的指示。

您认为批评者应该参加论文答辩，还是不参加答辩就接受论文并开始实际研究？我想您会有兴趣知道，相关系数的计算并不正确。批评是为了让材料更好，没有人认为文章是好的。这样，您的系统就不会获利太少，而是会获利更多。
123456789101112
新评论