Güzel görünüyor :)
Ama ne olduğunu ve nasıl kullanılacağını henüz çözemedim :)
Harika görünüyor :)
Ancak ne olduğunu ve nasıl kullanılacağını daha fazla anlamamız gerekiyor :)
ilk gizli katman olarak kullanılabilir - boyutsallık azaltma veya kümeleme için, olasılıksal ağlarda ve diğer birçok seçenekte kullanılabilir.
Materyal için teşekkürler!
Boş zamanlarımda öğrenmeye çalışacağım :)
İlginç bir ağ oluşturma yöntemi hakkındaki yeni makale için teşekkürler. Literatürü incelerseniz, yüzlerce olmasa da düzinelerce olduğunu görürsünüz. Ancak tüccarlar için sorun araç eksikliğinde değil, bunları doğru kullanmakta. Makale, bu yöntemi bir Uzman Danışman'da kullanmanın bir örneğini içeriyor olsaydı daha da ilginç olurdu.

İlginç bir ağ oluşturma yöntemi hakkındaki yeni makale için teşekkürler. Literatürü incelerseniz, yüzlerce olmasa da düzinelerce olduğunu görürsünüz. Ancak tüccarlar için sorun araç eksikliğinde değil, bunları doğru kullanmakta. Makale, bu yöntemi bir Uzman Danışman'da kullanmanın bir örneğini içeriyorsa daha da ilginç olurdu.
1. Makale iyi. Erişilebilir bir şekilde sunulmuş, kod karmaşık değil.
2. Makalenin dezavantajları arasında ağ için girdi verileri hakkında hiçbir şey söylenmemesi yer alıyor. Girdinin ne olduğu hakkında birkaç kelime yazabilirdiniz - dönem/gösterge verileri için fiyat teklifleri vektörü, fiyat sapmaları vektörü, normalleştirilmiş fiyat teklifleri veya başka bir şey. Algoritmanın pratik kullanımı için, girdi verileri ve bunların hazırlanması konusu kilit öneme sahiptir. Bu tür algoritmalar için göreceli fiyat değişiklikleri vektörü kullanmanızı öneririm: x[i]=fiyat[i+1]-fiyat[i].
Buna ek olarak, önceden girdi vektörü normalize edilebilir (x_normal[i]=x[i]/M), bunun için söz konusu dönem için fiyatın maksimum sapması M olarak kullanılabilir (burada ve aşağıda, kısalık için değişken bildirimlerini yazmıyorum):
M=x[ArrayMaximum(x)]-x[ArrayMinimum(x)];
Bu durumda, tüm girdi vektörleri [-0.5,0.5] kenarlı bir birim hiperküpte yer alacak ve bu da kümeleme kalitesini önemli ölçüde artıracaktır. Ayrıca standart normal sapmayı veya dönem boyunca fiyat tekliflerinin göreli sapmaları üzerindeki diğer ortalama değişkenlerini M olarak kullanabilirsiniz.
3. Makale, nöron ağırlıkları vektörü ile girdi vektörü arasındaki mesafe olarak farkın normunun karesinin kullanılmasını önermektedir:
for(i=0, sum=0; i<m; i++, sum+=Pow(x[i]-w[i],2));
Benim görüşüme göre, bu kümeleme görevinde bu mesafe fonksiyonu etkili değildir. Skaler çarpımı ya da normalize edilmiş skaler çarpımı, yani ağırlık vektörü ile girdi vektörü arasındaki açının kosinüsünü hesaplayan fonksiyon daha etkilidir:
for(i=0, norma_x=0, norma_w=0; i<m; i++, norma_x+=x[i]*x[i], norma_w+=w[i]*w[i]); norma_x=sqrt(norma_x); norma_w=sqrt(norma_w); for(i=0, sum=0; i<m; i++, sum+=x[i]*w[i]); if(norma_x*norma_w!=0) sum=sum/(norma_x*norma_w);
Daha sonra her kümede, salınımların yönlerine göre birbirine benzer vektörler gruplandırılacak, ancak bu salınımların büyüklüğüne göre değil, çözülecek problemin boyutluluğunu önemli ölçüde azaltacak ve eğitilmiş sinir ağının ağırlık dağılımlarının özelliklerini artıracaktır.
4.Ağı eğitmek için bir durdurma kriteri tanımlamanın gerekli olduğu doğru bir şekilde gözlemlenmiştir. Durdurma kriteri, eğitilen ağın gerekli küme sayısını belirlemelidir. Ve bu (sayı), sırayla, çözülecek genel probleme bağlıdır. Görev 1-2 örnek ilerisi için bir zaman serisini tahmin etmekse ve bu amaçla, örneğin, çok katmanlı bir perseptron kullanılacaksa, küme sayısı perseptronun giriş katmanının nöron sayısından çok farklı olmamalıdır.
Genel olarak, geçmişteki çubuk sayısı en ayrıntılı dakika grafiğinde 5.300.000'i geçmez (10 yıl*365 gün*24 saat*60 dakika). Saatlik grafikte bu sayı 87.000 çubuktur. Yani, küme sayısı 10000-20000'den fazla olan bir sınıflandırıcının oluşturulması, her bir teklif vektörünün kendi ayrı kümesi olduğunda "aşırı eğitim" etkisi nedeniyle haklı değildir.
Olası hatalar için özür dilerim.
1. Teşekkür ederim, sizin için elimden geleni yaptım:)
2. Evet, katılıyorum. Ancak yine de girdiler - bu ayrı bir büyük sorun, tek başına üzerine onlarca makale yazabilirsiniz.
3. Ve burada tamamen katılmıyorum. Normalize edilmiş girdiler söz konusu olduğunda, skaler çarpımların karşılaştırılması Öklid normlarının karşılaştırılmasına eşdeğerdir - formülleri genişletin.
4. Maksimum küme sayısı zaten algoritmanın parametrelerinden biri olduğu için.
max_nodes
Örneğin şu şekilde ilerlerdim: son N adımda kazananın hatasını ölçün ve dinamiklerini bir şekilde değerlendirin (örneğin, regresyon çizgisinin eğimini ölçün) Hata çok az değişirse, durun. Hata hala azalıyorsa ve eğitim verileri zaten tükenmişse, gürültüyü bastırmak veya bir şekilde örnek eksikliğini ortadan kaldırmak için düzeltmelerini düşünmeye değer.
3. Formüllerin eşdeğerliğinin nerede olduğunu anlamıyorum.(x,w)/(|x|||w|) vektörleri arasındaki açının kosinüsü için formül |x-w|^2'ye "pek" benzemez. Girdileri normalleştirmek bu ölçütler arasındaki temel farklılıkları değiştirmez:
Eşdeğerlik, mesafenin maksimumunun her zaman skaler çarpımın minimumuna karşılık gelmesi ve bunun tersinin de geçerli olmasıdır. Normalleştirilmiş vektörler durumunda ilişki karşılıklı olarak açık ve monotoniktir, bu nedenle mesafenin karesinin mi yoksa açının mı hesaplanacağı önemli değildir.
Merhaba Alex,
Konuyla ilgili net açıklama için teşekkürler.
Örneğin optimal sinyallerden gelecekteki fiyatı yeniden yapılandırmak için bazı pratik kodları paylaşmak mümkün olabilir mi?
Fikir şudur:
1. Giriş (Kaynak): çoklu para birimleri (18)
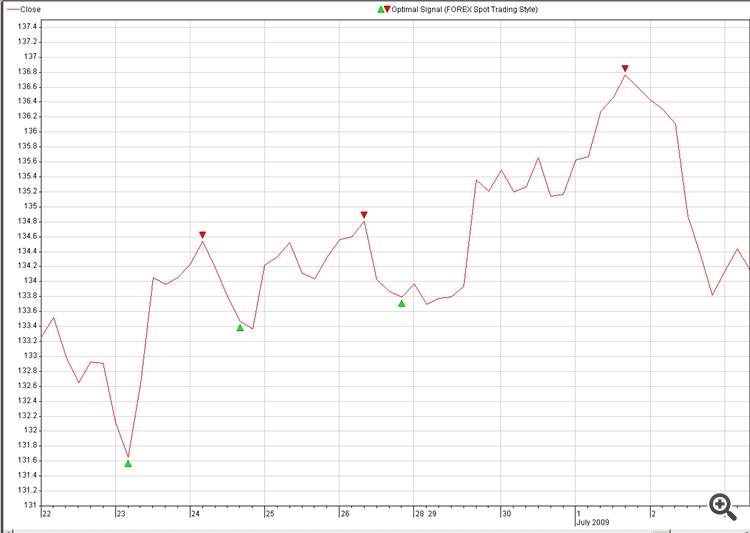
2. Hedef: Tahmin etmek istediğimiz para biriminin optimum sinyali (resim: 2. Optimal_Signals)
3. Kaynak ve Hedef arasında bir nöro-bağlantı bulun ve bunu ticarette patlatın.
NN yeniden yapılandırması hakkında başka bir soru:
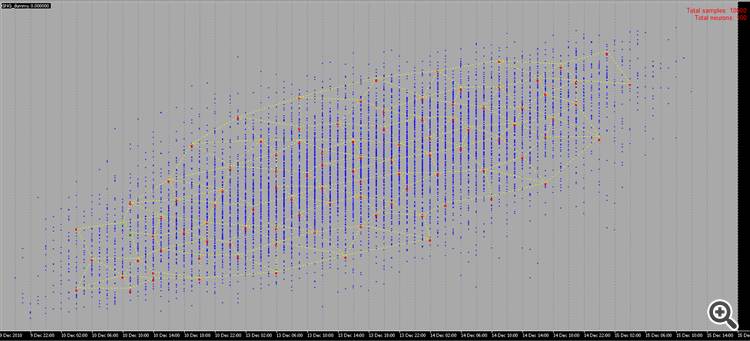
Rastgele Örnekler yerine, resim 2'deki gibi örneklerimizi kullanmak mümkün mü?
Beynimiz resmi bir saniyeden daha kısa bir sürede yeniden oluşturabilir, bakalım NN için aynı şeyi yapmak ne kadar zaman alacak, sadece bir şaka, bu bir meydan okuma değil.

Rastgele oluşturulan Örnekler, arkasında bir anlam veya kullanım olmadığı için görmek için çok ilginç değildir, ancak arkasındaki bazı anlamlarla noktaları kendimiz çizebilirsek, çok daha eğlenceli olurdu :-0)
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz
Yeni makale Büyüyen Nöral Gaz: MQL5'te Uygulama yayınlandı:
Makalede, Büyüyen nöral gaz (GNG) olarak adlandırılan uyarlanabilir kümeleme algoritmasını uygulayan bir MQL5 programının nasıl geliştirileceğine ilişkin bir örnek gösterilmektedir. Bu makale, dil belgelerini incelemiş ve nöroinformatik alanına ilişkin belirli programlama becerilerine ve temel bilgilere sahip kullanıcılara yöneliktir.
Algoritmayı programlarken, "kümeler" olarak adlandırılanları depolama ihtiyacıyla açık bir şekilde ilgilenmemiz gerekecek. İki kümemiz olacak; bir dizi nöron ve bunların arasında bir dizi kenar. Program süresince her iki yapı da gelişecek olsa da (ve hem öğe eklemeyi hem de çıkarmayı planlıyoruz), bunun için mekanizmalar da sağlamalıyız.
Elbette ki, nesnelerin dinamik dizilerini kullanmayı deneyebiliriz, ancak çok sayıda veri kopyalama-taşıma işlemi gerçekleştirmemiz gerekir; bu da programı yavaşlatır. Belirtilen özellikleri içeren soyutlamalarla çalışmak için daha uygun bir seçenek, program grafikleri ve bunların en basit sürümü olan bağlantılı bir listedir.
Okuyucularımıza bağlantılı listenin çalışma prensibini hatırlatacağım (Şek. 1). Temel sınıfın nesneleri, üyelerden biri ile aynı nesneye bir işaretçi içerir; bu da bellekteki nesnelerin fiziksel sırasına bakılmaksızın, onları doğrusal yapılarda birleştirmeye olanak tanır. Ayrıca, listede gezinme, düğüm ekleme, yerleştirme ve silme, arama, karşılaştırma ve sıralama ve gerekirse diğer prosedürleri içeren "taşıma" sınıfı vardır.
Yazar: Alexey Subbotin