Оптимизация алгоритмов.

Andrey Dik 2012.04.04 13:05

Предлагаю здесь обсуждать проблемы оптимального построения логики алгоритмов.

Если кто то сомневается, что его алгоритм имеет оптимальную по быстродействию (или по наглядности) логику, то добро пожаловать.

Так же приветствую в этой ветке тех, кто хочет поупражняться в алгоритмизации и помочь другим.

Первоначально задал свой вопрос в ветке "Вопросы от чайника", но понял, что там ему не место.

Итак, предложите, пожалуйста, более быстрый вариант алгоритма "рулетка" чем этот:

//——————————————————————————————————————————————————————————————————————————————
// Рулетка.
int Selection()
{
  //----------------------------------------------------------------------------
  int    i=0,u=0;
  double p=0.0,start=0.0;
  double          fit[][2];
  ArrayResize(fit,SizeOfPop);
  ArrayInitialize(fit,0.0);
  double delta=(Population[0][0]-Population[0][SizeOfPop-1])*0.1-Population[0][SizeOfPop-1];
  //----------------------------------------------------------------------------
  for(i=0;i<SizeOfPop;i++)
  {
    fit[i][0]=start;
    fit[i][1]=start+MathAbs(Population[0][i]+delta);
    start=fit[i][1];
  }
  p=RNDfromCI(fit[0][0],fit[SizeOfPop-1][1]);

  for(u=0;u<SizeOfPop;u++)
    if((fit[u][0]<=p && p<fit[u][1]) || p==fit[u][1])
      break;
    //--------------------------------------------------------------------------
  return(u);
}
//——————————————————————————————————————————————————————————————————————————————

понятно, что массивы можно вынести из функции что бы их не объявлять каждый раз и не ресайзить, но мне нужно более революционное решение. :)

[Удален] 2012.04.04 13:59 #1

joo

Для начала, думаю, необходимо привести код к:

1. Компилируемому виду.

2. Читабельному виду.

3. Комментариями.

В принципе, тема интересна и насущна.

Andrey Dik 2012.04.04 15:39 #2

voix_kas:

joo

Для начала, думаю, необходимо привести код к:

1. Компилируемому виду.

2. Читабельному виду.

3. Комментариями.

Ок.

Имеем отсортированный массив вещественных чисел. Нужно выбрать ячейку массива с вероятностью соответствующей размеру сектора воображаемой рулетки.

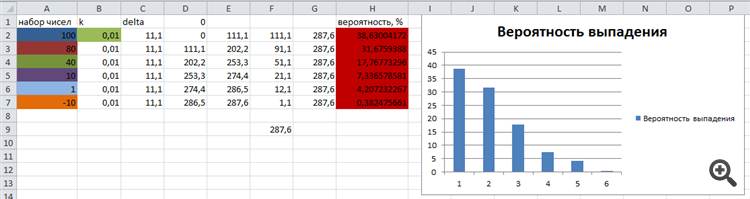
Тестовый набор чисел и теоретическая вероятность их выпадения рассчитаны в Excel и представлены для сравнения с результатами работы алгоритма на следующем рисунке:

Результат выполнения алгоритма:

2012.04.04 21:35:12    Roulette (EURUSD,H1)    h0 38618465    38.618465
2012.04.04 21:35:12    Roulette (EURUSD,H1)    h1 31685360    31.68536
2012.04.04 21:35:12    Roulette (EURUSD,H1)    h3 7334754      7.334754
2012.04.04 21:35:12    Roulette (EURUSD,H1)    h4 4205492      4.205492
2012.04.04 21:35:12    Roulette (EURUSD,H1)    h5 385095       0.385095
2012.04.04 21:35:12    Roulette (EURUSD,H1)    12028 мс - Время исполнения

Как видим, результаты вероятности выпадения "шарика" на соответствующем секторе практически совпадают с теоретическими рассчитанными.

#property script_show_inputs
//--- input parameters
input int StartCount=100000000;

// Границы соответствующих секторов рулетки
double select1[]; // начало сектора
double select2[]; // конец сектора
//——————————————————————————————————————————————————————————————————————————————
void OnStart()
{
  MathSrand((int)TimeLocal());// сброс генератора

  // массив с тестовым набором чисел
  double array[6]={100.0,80.0,40.0,10.0,1.0,-10.0};

  ArrayResize(select1,6);ArrayInitialize(select1,0.0);
  ArrayResize(select2,6);ArrayInitialize(select2,0.0);

  // счетчики для подсчета выпадений соответствующего числа из тестового набора
  int h0=0,h1=0,h2=0,h3=0,h4=0,h5=0;


  // нажмём кнопочку секундомера
  int time_start=(int)GetTickCount();

  // проведём серию испытаний
  for(int i=0;i<StartCount;i++)
  {
    switch(Roulette(array,6))
    {
    case 0:  h0++;break;
    case 1:  h1++;break;
    case 2:  h2++;break;
    case 3:  h3++;break;
    case 4:  h4++;break;
    default: h5++;break;
    }
  }

  Print((int)GetTickCount()-time_start," мс - Время исполнения");
  Print("h5 ",h5, " ",h5*100.0/StartCount);
  Print("h4 ",h4, " ",h4*100.0/StartCount);
  Print("h3 ",h3, " ",h3*100.0/StartCount);
  Print("h1 ",h1, " ",h1*100.0/StartCount);
  Print("h0 ",h0, " ",h0*100.0/StartCount);
  Print("----------------");
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Рулетка.
int Roulette(double &array[], int SizeOfPop)
{
  int    i=0,u=0;
  double p=0.0,start=0.0;

  double delta=(array[0]-array[SizeOfPop-1])*0.01-array[SizeOfPop-1];
//------------------------------------------------------------------------------
  // зададим границы секторов
  for(i=0;i<SizeOfPop;i++)
  {
    select1[i]=start;
    select2[i]=start+MathAbs(array[i]+delta);
    start=select2[i];
  }

  // бросим "шарик"
  p=RNDfromCI(select1[0],select2[SizeOfPop-1]);

  // посмотрим, на какой сектор упал "шарик"
  for(u=0;u<SizeOfPop;u++)
    if((select1[u]<=p && p<select2[u]) || p==select2[u])
      break;
//------------------------------------------------------------------------------
  return(u);
}
//——————————————————————————————————————————————————————————————————————————————

//——————————————————————————————————————————————————————————————————————————————
// Генератор случайных чисел из заданного интервала.
double RNDfromCI(double min,double max)
{return(min+((max-min)*MathRand()/32767.0));}
//——————————————————————————————————————————————————————————————————————————————

Файлы:

Roulette.zip 12 kb

Ваше мнение OpenCL в трейдинге Запись и чтение структур

Vladimir Gomonov 2012.04.04 16:41 #3

joo:

Ок.

Имеем отсортированный массив вещественных чисел. Нужно выбрать ячейку массива с вероятностью соответствующей размеру сектора воображаемой рулетки.

Объясни принцип задавания "ширины сектора". Он соответствует значениям в массиве? Или отдельно задаётся?

Это самый тёмный вопрос, всё остальное не проблема.

Второй вопрос: что за число 0.01 ? Откуда взято ?

Короче: Скажи где взять корректные вероятности выпадения секторов (ширину в долях от длины окружности).

Можно просто размер каждого сектора. При условии (по умолчанию) что отрицательных размеров не бывает в природе. Даже в казино. ;)

Давайте о чем нибудь Помогите научиться программировать. [АРХИВ]Любой вопрос новичка, чтоб

Andrey Dik 2012.04.04 17:01 #4

MetaDriver:

Объясни принцип задавания "ширины сектора". Он соответствует значениям в массиве? Или отдельно задаётся?

Ширина секторов не может соответствовать значениям в массиве, иначе не для любых чисел будет работать алгоритм.

Важно расстояние, на котором находятся числа между собой. Чем дальше все числа отстоят от первого, тем меньше вероятность их выпадения. По сути мы откладываем на числовой прямой отрезки, пропорциональные расстояниям между числами с поправкой на коэффициент 0,01 что бы у последнего числа вероятность выпадения не равнялась 0 как самого дальнего от первого. Чем больше коэффициент, тем более равные получаются сектора. Файл экселя в прикрепе, поэкспериментируй.

MetaDriver:

1. Короче: Скажи где взять корректные вероятности выпадения секторов (ширину в долях от длины окружности).

2. Можно просто размер каждого сектора. При условии (по умолчанию) что отрицательных размеров не бывает в природе. Даже в казино. ;)

1. Расчет теоретических вероятностей приведён в экселе. Первое число - наибольшая вероятность, последнее число - наименьшая вероятность но не равная 0.

2. Отрицательных размеров секторов не бывает никогда для любого набора числел, при условии что набор отсортирован по убыванию - первое число самое большое (будет работать и с самым большим в наборе но отрицательным числом).

Интерполяция, аппроксимация и иже Использование токсичных техник в И снова о сравнении

Vladimir Gomonov 2012.04.04 17:43 #5

joo:

зю: Важно расстояние, на котором находятся числа между собой. Чем дальше все числа отстоят от первого, тем меньше вероятность их выпадения. По сути мы откладываем на числовой прямой отрезки, пропорциональные расстояниям между числами с поправкой на коэффициент 0,01 что бы у последнего числа вероятность выпадения не равнялась 0 как самого дальнего от первого. Чем больше коэффициент, тем более равные получаются сектора. Файл экселя в прикрепе, поэкспериментируй.

В твоей схеме "от балды" задаётся вероятность самого маленького числа (вмч). Разумного обоснования нет.

// Поскольку "обосновать" трудновато. Всё нормально - между N гвоздями всего N-1 промежутков.

Поэтому у тебя она (вмч) зависит от также "от балды" взятого "коффициента". Почему 0.01 ? почему не 0.001 ?

Прежде чем делать алгоритм, нужно определиться с вычислением "ширины" всех секторов.

зю: Давай формулу вычисления "расстояний между числами". Которое число "первое"? Оно от себя на каком расстоянии? В эксел не посылай, я там был. Там путано всё на идеологическом уровне. Откуда вообще поправочный коэффициент и почему именно такой?

Выделенное красным вообще неправда. :)

Явление Христа народу - Объемы, волатильность и показатель Функция ReQuote. Вопрос к

Serj 2012.04.04 18:25 #6

так будет очень быстро:

int Selection() { return(RNDfromCI(1,SizeOfPop); }

На качестве алгоритма в целом не должно отразиться.

А если даже незначительно отразится, то за счет скорости такой вариант обгонит и по качеству.

Обсуждение статьи "Алгоритм генерации ? к опытным Любые вопросы новичков по

Andrey Dik 2012.04.04 18:30 #7

MetaDriver:

1. В твоей схеме "от балды" задаётся вероятность самого маленького числа (вмч). Разумного обоснования нет. Поэтому у тебя она (вмч) зависит от также "от балды" взятого "коффициента". Почему 0.01 ? почему не 0.001 ?

2. Прежде чем делать алгоритм, нужно определиться с вычислением "ширины" всех секторов.

3. зю: Давай формулу вычисления "расстояний между числами". Которое число "первое"? Оно от себя на каком расстоянии? В эксел не посылай, я там был. Там путано всё на идеологическом уровне. Откуда вообще поправочный коэффициент и почему именно такой?

4. Выделенное красным вообще неправда. :)

1. Да, от балды. Мне нравится этот коэффициент. Если тебе нравится другой, то использую другой - скорость алгоритма не изменится.

2. Определённость достигнута.

3. Ок. Имеем отсортированный массив чисел - array[], где самое большое число находится в array[0], и числовой луч с начальной точкой 0.0 (можно взять любую другую точку - ничего не изменится) и направленный в положительную сторону. Откладываем на луче отрезки таким образом:

start0=0 end0=start0+|array[0]+delta|

start1=end0 end1=start1+|array[1]+delta|

start2=end1 end2=start2+|array[2]+delta|

......

start5=end4 end5=start5+|array[5]+delta|

где:

delta=(array[0]-array[5])*0.01-array[5];

Вот и вся арихметика. :)

Теперь, если мы бросим "шарик" на наш размеченный луч, то вероятность попадания на определенный отрезок пропорциональна длине этого отрезка.

4. Потому что ты не то (не всё) выделил. Нужно выделять так: "По сути мы откладываем на числовой прямой отрезки, пропорциональные расстояниям между числами с поправкой на коэффициент 0,01 что бы у последнего числа вероятность выпадения не равнялась 0"

Поиск пары чисел оптимально Машинное обучение в трейдинге: От теории к практике

Andrey Dik 2012.04.04 18:33 #8

her.human:

так будет очень быстро:

int Selection() { return(RNDfromCI(1,SizeOfPop); }

На качестве алгоритма в целом не должно отразиться.

А если даже незначительно отразится, то за счет скорости такой вариант обгонит и по качеству.

Вы предлагаете просто выбрать элемент массива случайным образом? - так не учитывается расстояния между числами массива, а поэтому Ваш вариант никуда негодный.

Документация по MQL5: Основы языка / Переменные

www.mql5.com

Основы языка / Переменные - Документация по MQL5

Serj 2012.04.04 18:46 #9

joo:

проверить не сложно.

подтверждается экспериментально, что он негодный?

Andrey Dik 2012.04.04 18:49 #10

her.human:

подтверждается экспериментально, что он негодный?

конечно. очень хорошо подтверждается экспериментально.

1 2 3 4 5 6 7 8 ...10

Новый комментарий