Обсуждение статьи "Растущий нейронный газ - реализация на языке программирования MQL5"

Новый комментарий
 

Опубликована статья Растущий нейронный газ - реализация на языке программирования MQL5:

В статье приводится пример написания на языке MQL5 программы, реализующий адаптивный алгоритм кластеризации, называемый "Растущий нейронный газ" (Growing neural gas, GNG). Статья рассчитана на пользователей, изучивших документацию к языку, а также уже имеющих определенные навыки программирования и базовые знания в области нейроинформатики.


Автор: Алексей

 

Выглядит прикольно :)

А вот что это, и как использовать, надо разобраться еще :)

 
mrProF:

Выглядит прикольно :)

А вот что это, и как использовать, надо разобраться еще :)

использовать можно как первый скрытый слой - для снижения размерности или собственно кластеризации, можно в вероятностных сетях, ну и куча других вариантов.
 
alsu:
использовать можно как первый скрытый слой - для снижения размерности или собственно кластеризации, можно в вероятностных сетях, ну и куча других вариантов.

Спасибо за материал!

На досуге попытаюсь осилить :)

 

Спасибо за новую статью об интересном сетевом методе. Если порыться в литературе, их там десятки, если не сотни. Но проблема у трейдеров не в отсутствии иснтрументов, а в правильном их использовании. Статья была бы ещё интереснее если бы она содержала пример использования этого метода в советнике.

  

 
gpwr:

Спасибо за новую статью об интересном сетевом методе. Если порыться в литературе, их там десятки, если не сотни. Но проблема у трейдеров не в отсутствии иснтрументов, а в правильном их использовании. Статья была бы ещё интереснее если бы она содержала пример использования этого метода в советнике.

Согласен, пусть то будет советник, индикатор или скрипт - но что бы было видно не только как преобразуются данные через НС но начало и следствия происходящего, т.е. как НС классифицировав паттерны stoch даёт возможные развития событий будущего индикатора к примеру....
 

1. Статья хорошая. Изложено доступно, код не сложный. 

2. К недостаткам статьи можно отнести то, что совсем ничего не сказано про входные данные для сети. Можно было написать пару слов о том, что подается на вход - вектор котировок за период/данных индикатора, вектор отклонений цены, нормализованные котировки или что-то еще. Для практического использования алгоритма, вопрос исходных данных и их предподготовки является ключевым.  Я рекомендую использовать для таких алгоритмов вектор относительных изменений цены: x[i]=price[i+1]-price[i].

Кроме того, предварительно, входной вектор можно нормализовать(x_normal[i]=x[i]/M), для чего, в качестве M можно использовать максимальное отклонение цены за рассматриваемый период (здесь и далее для краткости не пишу объявления переменных): 

M=x[ArrayMaximum(x)]-x[ArrayMinimum(x)];

В этом случае, все входные векторы будут лежать в единичном гиперкубе со стороной [-0.5,0.5], что существенно увеличит качество кластеризации. В качестве M также можно использовать стандартное нормальное отклонение или любые другие усредняющие величины по относительным отклонениям котировок за период.

3. В качестве расстояния между вектором весов нейрона и входным вектором в статье предлагается использовать квадрат нормы разности: 

for(i=0, sum=0; i<m; i++, sum+=Pow(x[i]-w[i],2));

На мой взгляд, эта функция расстояния не эффективна, в данной задаче кластеризации. Более эффективной является функция вычисляющая скалярное произведение или нормализованное скалярное произведение, то есть косинус угла между вектором весов и входным вектором: 

for(i=0, norma_x=0, norma_w=0; i<m; i++, norma_x+=x[i]*x[i], norma_w+=w[i]*w[i]);
norma_x=sqrt(norma_x); norma_w=sqrt(norma_w); 
for(i=0, sum=0; i<m; i++, sum+=x[i]*w[i]);
if(norma_x*norma_w!=0) sum=sum/(norma_x*norma_w);

Тогда в каждом кластере будут сгруппированы векторы похожие друг на друга направлениями колебаний, но не величиной этих колебаний, что существенно уменьшит размерность решаемой задачи и повысит характеристики распределений весов обученной нейросети.

4. Было правильно замечено, что необходимо определить критерий останова обучения сети. Критерий останова должен определить необходимое число кластеров обученной сети. А оно (число), в свою очередь, зависит от общей решаемой задачи. Если задача в прогнозировании временного ряда на 1-2 отсчета вперед, и для этого будет использован, например, многослойный персептрон, то количество кластеров не должно сильно отличаться от количество нейронов входного слоя персептрона.

Гибридная нейросеть

В целом, количество баров в истории не превосходит 5 300 000 на самом подробном минутном графике (10 лет*365 дней*24 часа*60минут). На часовом графике - 87 000 баров. То есть создание классификатора с числом кластеров более 10000-20000 уже не оправдано из-за эффекта "переобученности", когда на каждый вектор котировок приходится свой отдельный кластер.

Прошу прощения за возможные ошибки.

 

1. Спасибо, для вас старался:)

2. Да, согласен. Но все таки входы - это отдельная большая проблема, по которой самой по себе можно не один десяток статей написать.

3. А вот здесь не соглашусь полностью. В случае нормализованных входов сравнение скалярных произведений эквивалентно сравнению евклидовых норм - разверните формулы. 

4. Поскольку максимальное число кластеров и так уже один из параметров алгоритма

max_nodes

то я бы действовал, например, так: измеряем ошибку победителя на N последних шагах и оцениваем каким-либо образом ее динамику (например, измеряем наклон регрессионной прямой) Если ошибка изменяется мало, то останов. Если же ошибка все еще уменьшается, а данные для обучения уже закончились, то стОит подумать об их сглаживании с целью подавления шумов, или каким-то образом устранить дефицит примеров.

 

3. Не понял, где эквивалентность формул. Формула косинуса угла между векторами (x,w)/ (|x||w|) "не очень" похожа на |x-w|^2. Нормализация входов не меняет принципиальных различий этих мер:

 

 

эквивалентность в том, что максимум расстояния всегда соответствует минимуму скалярного произведения и наоборот. Связь в случае нормализованных векторов взаимно однозначная и монотонная, поэтому что вычислять - квадрат расстояния или угол, неважно.

 

Привет, Алекс,

Спасибо за четкое объяснение темы.

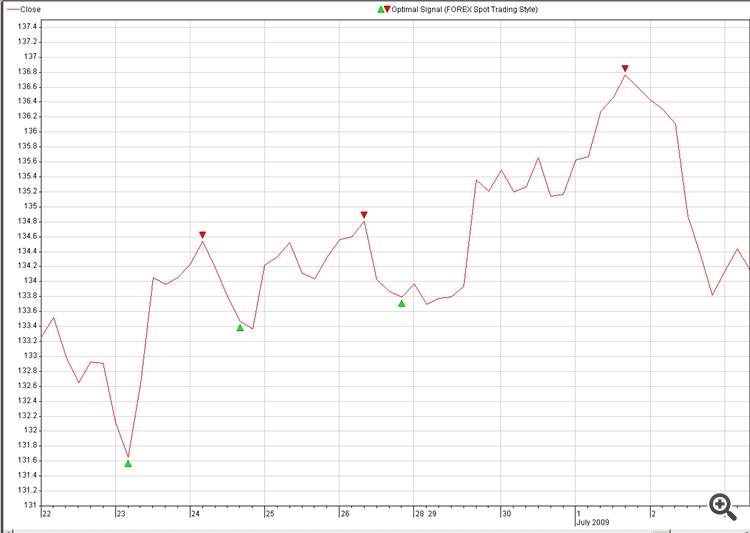
Не могли бы вы поделиться каким-нибудь практическим кодом для реконструкции будущей цены, например, из оптимальных сигналов.

Идея заключается в следующем:

1. Вход (источник): несколько валют (18)

2. Место назначения: Оптимальный сигнал валюты, которую мы хотим предсказать (рисунок: 2. Optimal_Signals)

3. Находим нейросвязь между Source и Destination и взрываем ее в торговле.


2. Оптимальные_сингналы


Еще один вопрос по поводу реконструкции NN:

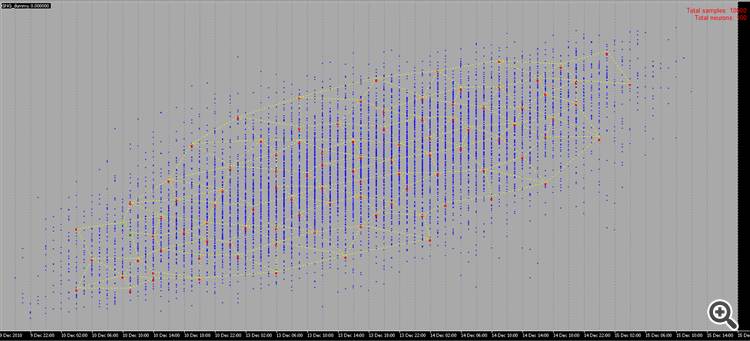
Можно ли вместо случайных образцов использовать наши образцы, как на рисунке 2:

Наш мозг может восстановить картинку менее чем за секунду, давайте посмотрим, сколько времени потребуется NN, чтобы сделать то же самое, просто шутка, это не вызов.

NN_Man


Случайно сгенерированные образцы не очень интересны для просмотра, так как за ними нет никакого смысла, однако если бы мы могли сами рисовать точки с каким-то смыслом, это было бы намного интереснее :-0)

GNG-1

12
Новый комментарий