Гармоническая скользящая средняя MAG
И чем она будет отличаться от Linear Weighted Moving Average (LWMA) — линейно-взвешенное скользящее среднее?
Отличается принципом присвоения весов и нахождения средней. Думаю, она должна отличаться бОльшим влиянием последних значений ценового ряда и сгладить основной недостаток скользящих средних - запаздывание. Сейчас попробую обработать имеющийся исторический материал на экзеле и выставить. Посмотрим на разницу MA и MAG.
Линейно-взвешенное скользящее среднее (Linear Weighted Moving Average, LWMA)
Во взвешенном скользящем среднем последним данным присваивается
больший вес, а более ранним — меньший. Взвешенное скользящее среднее
рассчитывается путем умножения каждой из цен закрытия в рассматриваемом
ряду на определенный весовой коэффициент.
LWMA = SUM (CLOSE (i) * i, N) / SUM (i, N)
Где:
SUM — сумма;
CLOSE(i) — текущая цена закрытия;
SUM (i, N) — сумма весовых коэффициентов;
N — период сглаживания.
В нашем случае весовой коэффициент задается по принципу гармонического ряда.
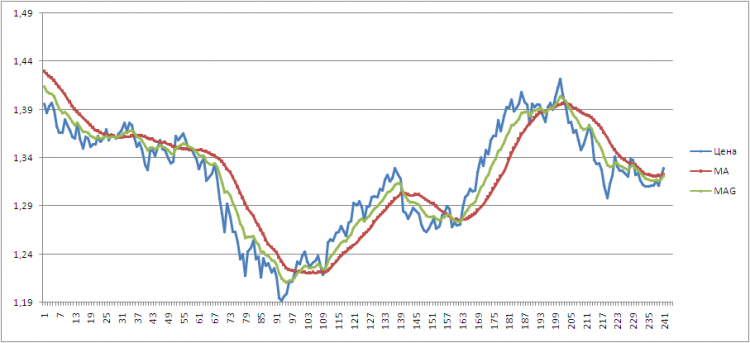
Вот обработка фактических данных по евро/доллару за 2010 г. на ТФ Д1, период МА и MAG =20:
Видно, что MAG более приближена к цене, чем МА и, следовательно, меньше запаздывает. Но, Вам виднее. Жду Вашей реакции.
Отличается принципом присвоения весов и нахождения средней. Думаю, она должна отличаться бОльшим влиянием последних значений ценового ряда и сгладить основной недостаток скользящих средних - запаздывание. Сейчас попробую обработать имеющийся исторический материал на экзеле и выставить. Посмотрим на разницу MA и MAG.
Линейно-взвешенное скользящее среднее (Linear Weighted Moving Average, LWMA)
Во взвешенном скользящем среднем последним данным присваивается больший вес, а более ранним — меньший. Взвешенное скользящее среднее рассчитывается путем умножения каждой из цен закрытия в рассматриваемом ряду на определенный весовой коэффициент.
Где:
SUM — сумма;
CLOSE(i) — текущая цена закрытия;
SUM (i, N) — сумма весовых коэффициентов;
N — период сглаживания.
В нашем случае весовой коэффициент задается по принципу гармонического ряда.
Вот обработка фактических данных по евро/доллару за 2010 г. на ТФ Д1, период МА и MAG =20:
Видно, что MAG более приближена к цене, чем МА и, следовательно, меньше запаздывает. Но, Вам виднее. Жду Вашей реакции.
Согласен что более приближена. Но и более неровная.
Благодарю за код индикатора. Действительно, более неровная из-за того, что, более чувствителен к последним изменениям цены, но, своеобразно учитывает, также, более ранние значения цены в пределах выбранного периода. Теперь, участники могут попробовать заменить в советниках, использующих МА на MAG и выявлять его сравнительную эффективность, если она значимо будет отличаться.
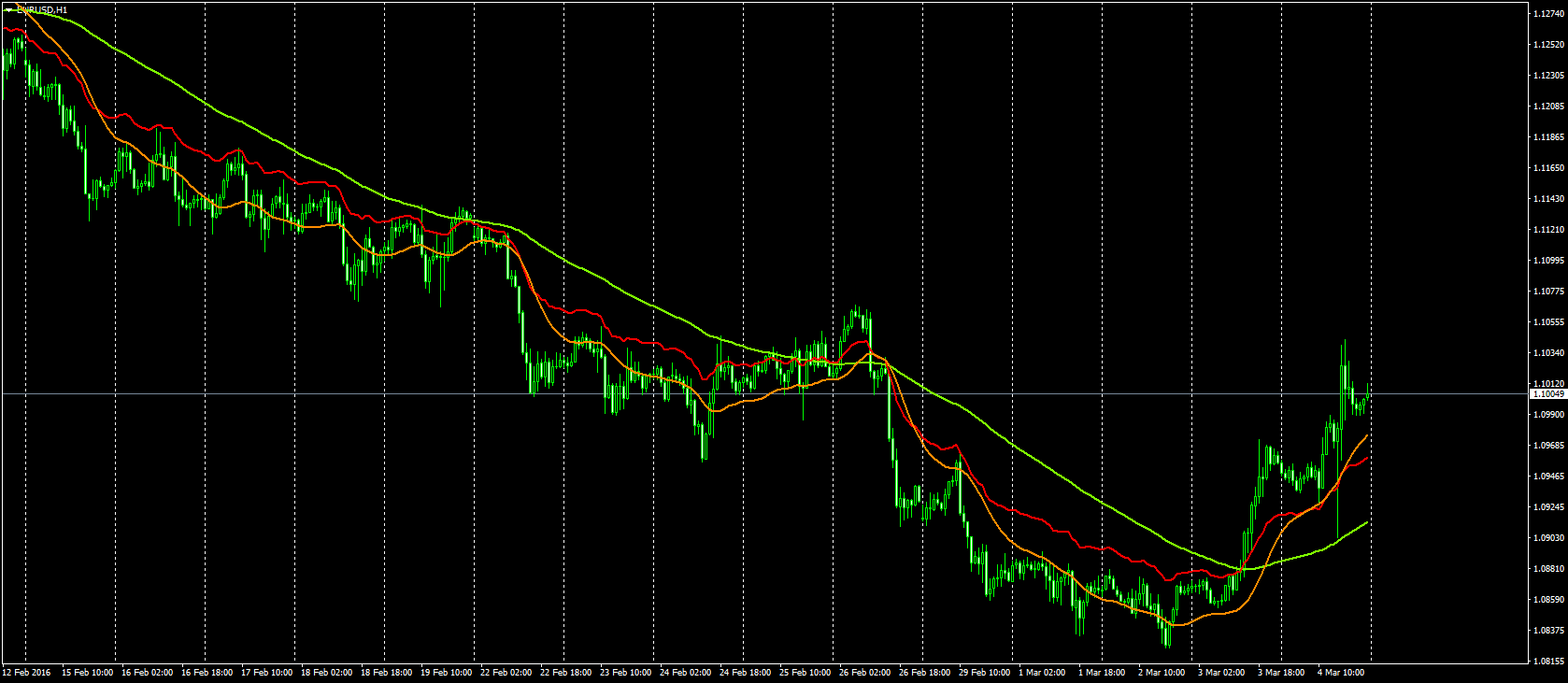
Поинтереснее вариант есть
Виктор, Вы здесь мой индикатор MAG сравниваете со скользящим средним Халла (Hull) HMA? Ну, и какие впечатления? Я восхищен Вашим усердием в вопросе исследования MAG. Благодарю.
Эффект от НМА иногда объясняют на сл. примере:
возьмем 10 чисел (периодов) от 0 до 9. Среднее арифметическое этих
чисел, то есть значение простой скользящей средней будет составлять 4,5:
МА=(0+1+2+...+10)/10 =4,5
Среднее число 4,5 значительно отстает от последнего числа 9. Если представить, что вместо этих цифр будут значение цены, видим, как она отстает от реальной цены.
Алан Халл предложил сократить в два раза срок (общий период), то есть применил расчет средней к последним пяти числам:
(5+6+7+8+9)/5 = 7
В результате получили число 7, это уже куда ближе к фактической цене,
но на этом Алан не остановился, он добавил к числу разницу между двумя
средними числами 2,5 (7–4,5=2,5). В итоге получили 9,5 (7+2,5), с
излишней перекомпенсацией на 0,5. Но эта сверхкомпенсация возмещает
результат отставания вложенного в усреднение. В итоге Алан Халл нашел
идеальный баланс между запаздыванием и сглаживанием, что практически
исключило отставания скользящей средней от цены. (источник есть, при желании, можете погуглить и найти)
Если то-же самое проделать с MAG, то получим:
MAG=(0/10+1/9+.....+9/1)/(1/1+1/2+....+1/10) = 6,3343
Чтобы ещё сильнее приблизиться к текущей цене, нам достаточно увеличить этот показатель в 1,5 раза:
MAG(1.5) = 1.5*MAG=1.5*6.3343=9.5
Т.е, мы получили точно такой-же результат, как и Алан Халл, применив одинаковый принцип присвоения весового коэффициента ко всему ряду, тогда, как Халл применил разные принципы к частям ряда. Поэтому, предполагаю, что MAG(1.5) должен превзойти HMA по основным показателям.
Виктор, прошу Вас, проверить эту гипотезу, введя изменения в код MAG. Или ещё кардинальнее - ввести настроечный параметр, допустим, S и, в частности, присвоить S=1.5. Тогда, в общем случае будет MAG(N,S), где N -период, а S - степень весового коэффициента или быстродействия (условно).
MAG(N,S) = S*MAG = S*(Ц1/N+W2/(N-1)+.....+ЦN/1)/(1/1+1/2+.....+1/N)
В частности, MAG(N,1) = MAG
Введение в настройки параметра S позволит поднимать или опускать линию MAG по отношению к графику цен и выбрать наилучшее состояние.
Виктор, Вы здесь мой индикатор MAG сравниваете со скользящим средним Халла (Hull) HMA? Ну, и какие впечатления? Я восхищен Вашим усердием в вопросе исследования MAG. Благодарю.
Эффект от НМА иногда объясняют на сл. примере:
возьмем 10 чисел (периодов) от 0 до 9. Среднее арифметическое этихчисел, то есть значение простой скользящей средней будет составлять 4,5:
МА=(0+1+2+...+10)/10 =4,5
Среднее число 4,5 значительно отстает от последнего числа 9. Еслипредставить, что вместо этих цифр будут значение цены, видим, какона отстает от реальной цены.
Алан Халл предложил сократить в два раза срок (общий период), то есть применил расчет средней к последним пяти числам:
(5+6+7+8+9)/5 = 7
В результате получили число 7, это уже куда ближе к фактической цене,но на этом Алан не остановился, он добавил к числу разницу между двумясредними числами 2,5 (7–4,5=2,5). В итоге получили 9,5 (7+2,5), сизлишней перекомпенсацией на 0,5. Но эта сверхкомпенсация возмещаетрезультат отставания вложенного в усреднение. В итоге Алан Халл нашелидеальный баланс между запаздыванием и сглаживанием, что практическиисключило отставания скользящей средней от цены. (источник есть, при желании, можете погуглить и найти)
Если то-же самое проделать с MAG, то получим:
MAG=(0/10+1/9+.....+9/1)/(1/1+1/2+....+1/10) = 6,3343
Чтобы ещё сильнее приблизиться к текущей цене, нам достаточно увеличить этот показатель в 1,5 раза:
MAG(1.5) = 1.5*MAG=1.5*6.3343=9.5
Т.е, мы получили точно такой-же результат, как и Алан Халл, применив одинаковый принцип присвоения весового коэффициента ко всему ряду, тогда, как Халл применил разные принципы к частям ряда. Поэтому, предполагаю, что MAG(1.5) должен превзойти HMA по основным показателям.
Виктор, прошу Вас, проверить эту гипотезу, введя изменения в код MAG. Или ещё кардинальнее - ввести настроечный параметр, допустим, S и, в частности, присвоить S=1.5. Тогда, в общем случае будет MAG(N,S), где N -период, а S - степень весового коэффициента или быстродействия (условно).
MAG(N,S) = S*MAG = S*(Ц1/N+W2/(N-1)+.....+ЦN/1)/(1/1+1/2+.....+1/N)
В частности, MAG(N,1) = MAG
Введение в настройки параметра S позволит поднимать или опускать линию MAG по отношению к графику цен и выбрать наилучшее состояние.
Точнее и глаже аппроксимации МНК y=b0+b1*x+b2*x*x. Вот 3 МА и 2 параболы: слева красная 50 и справа желтая 40 баров. точный ПРОГНОЗ
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
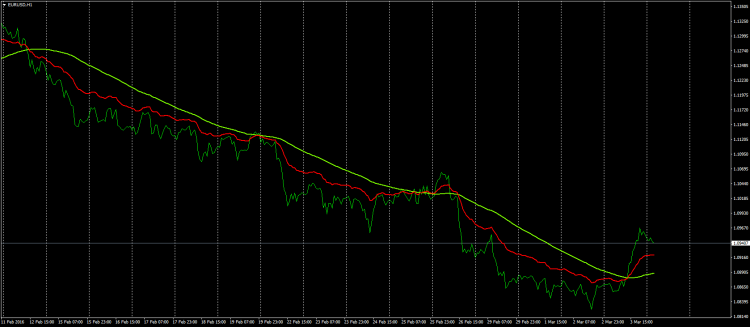
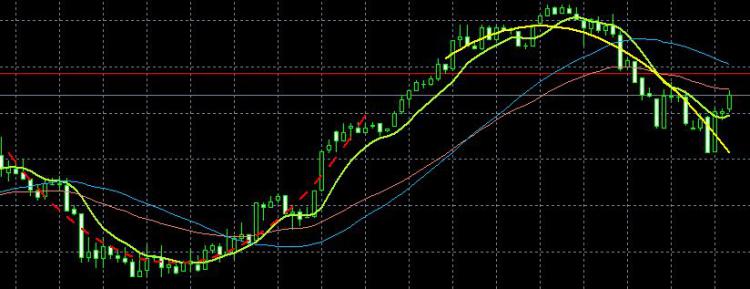
Уважаемые форумчане! Кто-нибудь встречал подобное, когда при нахождении скользящей средней упор делается именно на последние значения ценового ряда? Поясню на принципе определения обыкновенного скользящего среднего (MA) и гармонического скользящего среднего (MAG):
MA=(Ц1+Ц2+........+Ц(n-1)+Цn)/n
MAG=(Ц1/n+Ц2/(n-1)+........+Ц(n-1)/2+Цn/1)/(1/1+1/2+........+1/(n-1)+1/n)
Ц1 - первое значение ценового ряда;
Цn - последнее значение ценового ряда;
n - период MA или MAG.
Думаю, MAG должна иметь меньшее запаздывание, чем МА.
Вот пример исполнения:
Прошу программистов, предложенное воплотить в код индикатора MAG и выложить здесь, если подобное еще не выполнено, заранее благодарю.