Вопрос к знатокам теории вероятностей. - страница 4

Новый комментарий
 

simpleton:

Для проверки - а верна ли формула или метод расчёта, которые он найдёт?

Мне бы лично явно был нужен инструмент такой проверки. Заодно и прямые результаты на малых величинах.


Ещё раз повторюсь:


//+------------------------------------------------------------------+
//|                                                  spreadmodel.mq4 |
//|                                                               Hs |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Hs"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property strict
#property script_show_inputs
//--- input parameters
input int      MaxStartingMoney=30;
input int      MaxSteps=2000;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   int n,i,size,money;
   double c[]; // элемент c[i] равен вероятности, что баланс достигнет величины i
   size=MaxStartingMoney+MaxSteps+1;
   ArrayResize(c,size);
   for(money=1;money<=MaxStartingMoney;money++)
     {
      for(i=0;i<size;i++)
        {
         c[i]=0;
        }
      c[money]=1; // в начале баланс равен money с вероятностью 1
      for(n=1;n<=MaxSteps;n++) 
        {
         for(i=size-1;i>1;i--) // а здесь в двух циклах мы "раздваиваем" содержимое массива
           {                   // и смещаем его две копии на 1 шаг выше и на 1 шаг ниже,
            c[i]=c[i-1]/2;     // причём из ячейки с[0] содержимое не забирается,
           }                   // т.к. если игрок проиграл, то он далее в процессе не участвует
         c[1]=0; // собственно, баланса, равного 1, достичь можно, только если он был равен 2, но не 0
         for(i=0;i<size-2;i++)
           {
            c[i]+=c[i+2];
           }
         if(c[0]>=0.5) break; 
        }
      Print("Баланс: ",money,", Прошло: ",n,", Вероятность=",c[0]);
     }
  }
//+------------------------------------------------------------------+

 В результате "время полуслива" примерно равно 1.4826*sqrt(money).

 
Awwl:


Ещё раз повторюсь:


 В результате "время полуслива" примерно равно 1.4826*sqrt(money).

Насколько ваш вариант интересен и подходит topic-starter'у в его исследованиях - ему и решать.

А я, в целом, отвечал на следующий вопрос (хотя, возможно, цитату немного не ту использовал при ответе):

david2:

Хорошо! Как рассчитать вероятность того, что при 22 бросках будет минимум 16 решек.

И утверждаю, что вероятность данного события по определению вероятности самым строгим образом равна 110056 / 4194304, что примерно равно 0.02623939514160156. Это было вычислено с помощью программы, которая была составлена, опираясь на определение вероятности. Более того, немного "поигравшись" в диапазоне до 30 бросков, могу с уверенностью ответить и на следующий вопрос topic-starter'а:

david2:


Конечно если при увеличении количества бросков вероятность стремится от 0.001 к 0.5 а не 1, то все мои мысли бесполезны. Но я в этом сильно сомневаюсь.  

При увеличении количества бросков вероятность, совершенно очевидно, стремится именно к 0.5.

Если topic-starter (и другие читающие) заинтересуются вашим ходом мысли - кто ж им помешает?

 

Если эта задача ещё у кого-то вызывает интерес…

david2:

Имеем 10 монет. Играем в орел решку. Каждая ставка 1 монета. Ставим постоянно на орел. Если 10 раз подряд выпадет решка потеряем всю сумму(вероятность мала). Если кидаем до 2000 раз и 995 раз выпадет орел, а 1005 раз решка тоже проиграем всю сумму (вероятность высока, учитывается также вероятность проигрыша до достижения 2000 бросков). Как определить количество бросков, чтобы количество решки было на 10 больше орла и чтобы при этом вероятность данного события была ровна 0.5 

david2:


Неужели в процессе 10000 бросков количество выпадания решки ни разу не будет превосходить количество выпавших орлов всего на 10 единиц. Я думаю при таком количестве бросков вероятность данного события практически =1. Чтобы нужное нам событие произошло при 10 бросках, надо чтобы решка выпала 10 раз подряд.

Вероятность выпадания решки 10 раз подряд =0.5*0.5*0.5*0.5*0.5*0.5*0.5*0.5*0.5*0.5=0.001

Между 10 и 10000 должно быть то количество сделок где вероятность =0.5 

Есть ли программа, которая делает расчеты по формуле Бернулли?

Хотя все равно получится слишком трудоемкий процесс. Например если мы подозреваем что это количество сделок=150. То придется рассчитать не только вероятность выпадения решки минимум 80 раз при 150 бросках, но также 80 раз при 149, 79 раз при 148 итд.  

…то предлагаю примерное решение в непрерывном случае.

 Пусть график цены представляет собой винеровский процесс W с непрерывным временем t ≥ 0 и начальным значением 0, причём значения W(t) распределены согласно нормальному закону N(0, t) (где N(μ, σ²) — нормальное распределение со средним μ и дисперсией σ²). Плотность вероятности распределения в зависимости от времени равна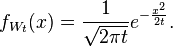 

Воспользуемся уравнением теплопроводности, в котором u = u(x, t) — функция распределения тепла, аргумент х задан на всей числовой прямой, а время t неотрицательно. При начальных условиях

 (δ — дельта-функция) решение выглядит так:

 

Теперь представим, что u(x, t) — плотность вероятности нахождения цены в момент времени t ≥ 0, и пусть при t=0 она равна δ(x-a), где параметр a>0, таким образом ценовой график начинается от значения а (при t=0 вероятность того, что Price=a, равна 1) и дальше блуждает случайно. Пусть также имеются граничные условия: х ≥ 0; u(0, t) = 0. Это означает, что точка x=0 является "местом утечки вероятности", т.е., условно говоря, из большого множества игроков игрок, добравшийся до х=0, терпит слив и выбывает из множества. Решение задачи в этом случае известно:

Здесь g(x) — начальное распределение вероятности.

Подставив g(x) = δ(x-a), получим:

 

Проинтегрировав это выражение по переменной х от 0 до +∞, мы узнаем суммарное количество "тепла", оставшегося на интервале [0; +∞), в зависимости от времени, т.е. получим вероятность "не слиться". Для получения вероятности "слиться" (или количества тепла, ушедшего через точку 0) вычтем результат из единицы. После упрощения получается:


Здесь erf() — лапласовская функция ошибок. Это и есть аналитическое решение нашей задачи, как-то так.

Картинки (c) Википедия 

1234
Новый комментарий
Причина обращения: