Да уж, пока не очень понятно, к чему эта задачка. Неужели трейдерам приходится решать такие задачи? ОК, сначала - рисунок.
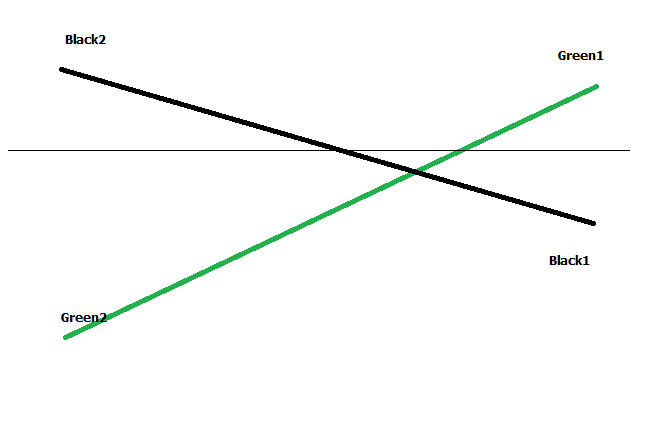
Точки с индексом 2 - это на баре 2, соответственно с индексом 1 - на баре 1. Пересечение где-то между барами, но уровень неизвестен.
Black1, Black2, Green1, Green2 - это значения линий.
Значение черной линии в точке Х (точке пересечения) равно (1-k) * Black2 + k * Black1 при некотором k. (1) Проще записать это как Black2 + k * (Black1 - Black2) и постепенно увеличивать k от 0 (левый конец отрезка) до 1 (правый), чтобы понять, как оно изменяется слева направо.
С другой стороны, значение зеленой в той же точке равно (1-k) * Green2 + k * Green1 = Green2 + k * (Green1 - Green2). (2)
Значения k в обоих случаях должны быть равны - в силу того, что и зеленый, и черный отрезок делятся в равных пропорциях в точке пересечения. Решаем уравнение относительно k, приравнивая выражения (1) и (2):
Black2 + k * (Black1 - Black2) = Green2 + k * (Green1 - Green2).
Решив его, дальше подставьте его в любое из выражений (1) или (2) и сравните с нулем.Надеюсь, поможет...
))
пр аппроксимации отрезками ордината точки пересечения
y=(Green1+Green2+Black1+Black2)/4
))
пр аппроксимации отрезками ордината точки пересечения
y=(Green1+Green2+Black1+Black2)/4
или нет?
Я бы сделал именно так и не парился с "суперточностью".
А топикстартеру хочется дать совет : не можете сами посчитать место пересечения двух точек - бегите подальше от форекса. Ну если уж точнее - от программирования торговых систем. Иначе вас форекс без трусов оставит. Вам оно нада?
А топикстартеру хочется дать совет : не можете сами посчитать место пересечения двух точек - бегите подальше от форекса. Ну если уж точнее - от программирования торговых систем. Иначе вас форекс без трусов оставит. Вам оно нада?
Злой ты ).
До форекса дело может и не дойдёт.
А решение такого плана задачек- для головы полезно.
Сколько человек узнали о преобразовании Фурье благодаря форексу?!
PS:
Пересечение- это когда обе линии задаются уравнениями
y = kx + b
k и b нужно найти.
Шаг x = 1 (1 бар)-
x1 = 0 (предыдущий бар), x2 = 1 (текущий бар).
Находится x пересечения, от него- y пересечения.
Кому задачку?! Я решал именно с kx + b... ))

))
пр аппроксимации отрезками ордината точки пересечения
y=(Green1+Green2+Black1+Black2)/4
Нет. Проверка, как всегда предельным переходом: для двух параллельных прямых. По такому расчету точку можно найти, а реально ее нет.
alsu:
))
пр аппроксимации отрезками ордината точки пересечения
y=(Green1+Green2+Black1+Black2)/4
или нет?
Нет. Проверка, как всегда предельным переходом: для двух параллельных прямых. По такому расчету точку можно найти, а реально ее нет.
2 ТС: А что мешает найти точку пересечения (ф-ция Кима годится) и посмотреть на значение ординаты (t[1]) - больше или меньше нуля ?
Точка пересечения диагоналей - центр тяжести системы из его вершин? Нет. Контрпример - когда пересечение в точности на правом конце.
P.S. Кстати, основное уравнение не всегда решается:
Black2 + k * (Black1 - Black2) = Green2 + k * (Green1 - Green2)
Если к-ты при k одинаковы, а свободные члены разные (как раз случай параллельности и неидентичности прямых), то решений нет.
Конечно, правильно еще и убедиться в том, что пересечение было между левым и правым концом. Но это совсем просто.
Точка пересечения диагоналей - центр тяжести системы из его вершин? Нет. Контрпример - когда пересечение в точности на правом конце.
Безусловно эта формула не точна. Но меня бы устроила.
--
более точную формулу можно найти так:
берём центры боковых сторон. рисуем линию между ними. точка пересечения находится на ней.
находим теперь линейную комбинацию для определения "где именно": p = abs(green1-black1) / abs(green2-black2);
значит наши коэффициенты равны p и (1-p) соответственно.
отсюда искомый X = sign(((green1+black1)/2)*p + ((green2+black2)/2)*(1-p))
Если точка пересечения есть (простое условие)- то все хорошо
В принципе тогда можно и так:
if( (Black2Y-Grin2Y)*(Black1Y-Green1Y)<0 )
y=(Green1Y+Green2Y+Black1Y+Black2Y)/4;
else return(Нет пересечения на интересующем участке);
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Народ, 100% вопрос уже ни раз приходилось решать большинству из Вас, помогите, как научить индикатор определять положение точки пересечения 2-х линий относительно линии 0 ???
Банальная проверка типа одно значение до пересечения больше другого, а после пересечения наоборот, не работает, т.к. это же правило сработает и при разностороннем движении линий инди.
Я вижу визуально, что линии пересеклись, и мне надо точно знать, где находится т.ПЕРЕСЕЧЕНИЯ этих 2-х линий - ВЫШЕ 0 или НИЖЕ.
Неужели придется использовать мат.формулы для расчета точки пересечения 2-х функций, с последующим сравнением с 0?
Заранее очень сильно благодарю!!