Olá a todos...
Tenho uma pergunta sobre a transformação de Fourier...
Após a transformação de Fourier e a filtragem de passagem alta com transformada reversa,
Preciso continuar calculando a função resultante fora do alcance da transformação (se você puder dar um exemplo)...
Nada mais precisa ser calculado, pois a transformação de Fourier só é efetivamente aplicada a funções periódicas.
Suponhamos que tenhamos um sinal periódico sobre o alcance obtido,
a consequência é que o início da matriz é uma continuação da seqüência periódica. Certo?
Suponhamos que tenhamos um sinal periódico sobre o alcance obtido,
a consequência é que o início da matriz é uma continuação da seqüência periódica. >> certo?
Que tipo de conjunto?
A transformação de Fourier é realizada no período aproximado de 0 a 2 * PI.
2*PI é de 0 graus para o próximo período para o qual a aproximação já foi realizada no período anterior.
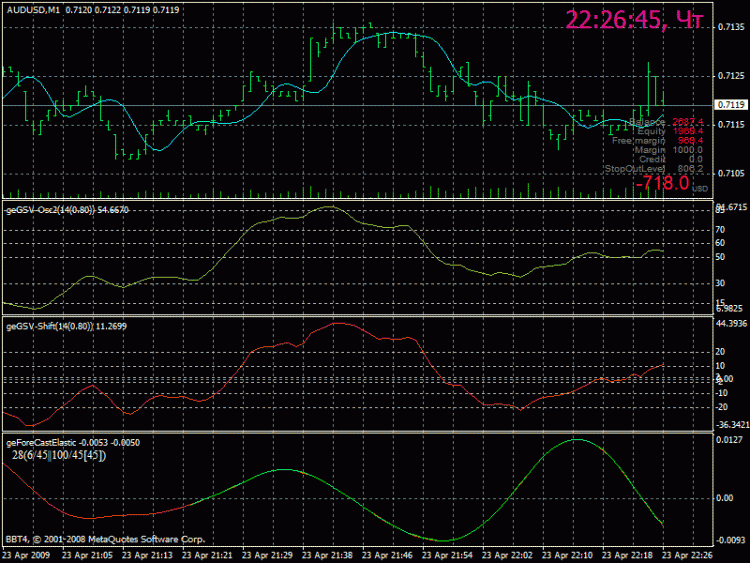
Então vejamos a figura...
A curva (vermelha) no visor inferior é a linha verde obtida no processo de conversão com os seguintes parâmetros
o tamanho da janela de conversão 2^6=64 pontos, o número de freqüências utilizadas é 45.
ou seja, obtemos uma semblante da curva resultante ... que impusemos ao original ...
como você pode ver pela figura, substituir o início pelo fim não é um resultado real -
Portanto, a questão é como continuar a curva, como mostra a linha verde.
....
Portanto, a questão é como continuar o movimento da curva mostrada pela linha verde.
Esse é o truque com Fourier e transformações similares!
Primeiro você traz a não-estacionariedade do mercado para uma forma quase-estacionária, pelo menos...
Então você pode transformar tudo em ondas sinusoidais estacionárias e continuar onde você quiser. Mas... Você provavelmente não vai chegar a lugar algum...
Talvez devêssemos então colocar a questão de uma maneira diferente.
Qual é a melhor maneira de aproximar a função mostrada na figura para que a curva possa ser continuada em uma pequena área?
Em uma pequena área qualquer método de aproximação pode ser usado, usando-o para extrapolar.
Eu uso o Lagrangiano.
Então vejamos a figura...
A curva (vermelha) no visor inferior é a linha verde obtida no processo de conversão com os seguintes parâmetros
o tamanho da janela de conversão 2^6=64 pontos, o número de freqüências utilizadas é 45.
ou seja, obtemos uma semblante da curva resultante ... que impusemos ao original ...
como você pode ver pela figura, substituir o início pelo fim não é um resultado real -
Portanto, a questão é como continuar o movimento da curva mostrada pela linha verde.
1. Por que diabos você decidiu que os 64 pontos tomados para a aproximação são uma função periódica?
2. O número de harmônicas não pode exceder a metade das amostras coletadas, ou seja, se a aproximação por 64 divisões de período, a harmônica máxima será de 31º.
3. Resultado irrealista porque você assumiu uma função não periódica de aproximação e, portanto, a continuação do período não corresponderá. Já lhe foi dito que o PF é eficaz apenas em funções periódicas, tudo o mais é um jogo de pandeiro.
Você deve tomar dois períodos idênticos: 0 - 2*PI, 2*PI - 4*PI. Use ambos para gerar PF e comparar se houver uma correspondência em amplitudes e fases de harmônicas. Caso contrário, significa que a função não é periódica e que o período de amostragem deve ser aumentado ou diminuído (diminuição ou aumento - isto é, observar as mudanças de fase para os harmônicos individuais)
Todo o resto é só dançar com pandeiro.
É necessário tomar dois períodos idênticos: 0 - 2*PI, 2*PI - 4*PI. Para ambos, é necessário dobrar o PF e comparar se há uma correspondência em amplitudes e fases de harmônicas. Se não, significa que a função é não periódica e o período de amostragem deve ser aumentado ou diminuído (diminuição ou aumento depende dos turnos de fase dos harmônicos individuais)
Em princípio, isto também é "dança de tamborim", apenas com mais "artifício". O resultado será uma história "mais bonita" - nada mais.
O periódico é uma função para a qual existe T tal que para qualquer x a seguinte igualdade f(x) = f(x+T) é verdadeira. Então T é o período da função f(x).
Simplificando - o trader não tem garantia de que quando T for escolhido de acordo com o algoritmo sugerido (como um múltiplo comum de dois períodos consecutivos), o terceiro período do mesmo tamanho de amostra corresponderá ao valor selecionado (e o terceiro é apenas o período, para o qual a extrapolação é feita). Não há nenhuma garantia com nenhum algoritmo para selecionar T.
E, a propósito - se a função é periódica - por que precisamos deste Fourier? Nunca ninguém pensou sobre isso? Encontrar um período e apenas valores substitutos, isso é tudo ;). Isto é, claro, se você encontrou o período e não dançou com tamborim....
>> Boa sorte com isso.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Olá a todos...
Tenho uma pergunta sobre a transformação de Fourier...
Após a transformação de Fourier e a filtragem de passagem alta com transformada reversa,
você quer continuar calculando a função resultante fora do alcance da transformação (se você puder dar um exemplo)...